
- •Прямоугольная декартова система координат на плоскости
- •Билет 3
- •Билет 8
- •Геометрические свойства скалярного произведения
- •Геометрический смысл векторного произведения
- •Свойства. Формула Лагранжа
- •Билет 12 Прямая на плоскости
- •Билет 14 Полные и неполные уравнения прямой
- •5. Условия перпендикулярности двух прямых:
- •Билет 18
- •Билет 24 Прямая в пространстве
Билет 8
Скалярное произведение
Скалярным
произведением
на
называется число
![]() .
.
Второе
определение:
![]() .
.
Оба определения
равносильны, т.к.
![]() ,
,
![]() .
.
Алгебраические свойства скалярного произведения:
 .
.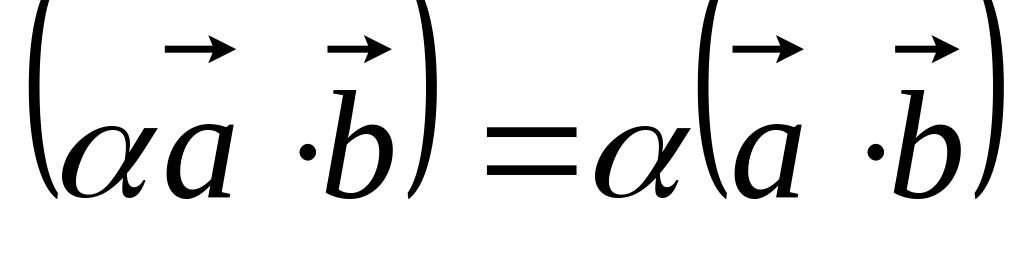 .
. .
.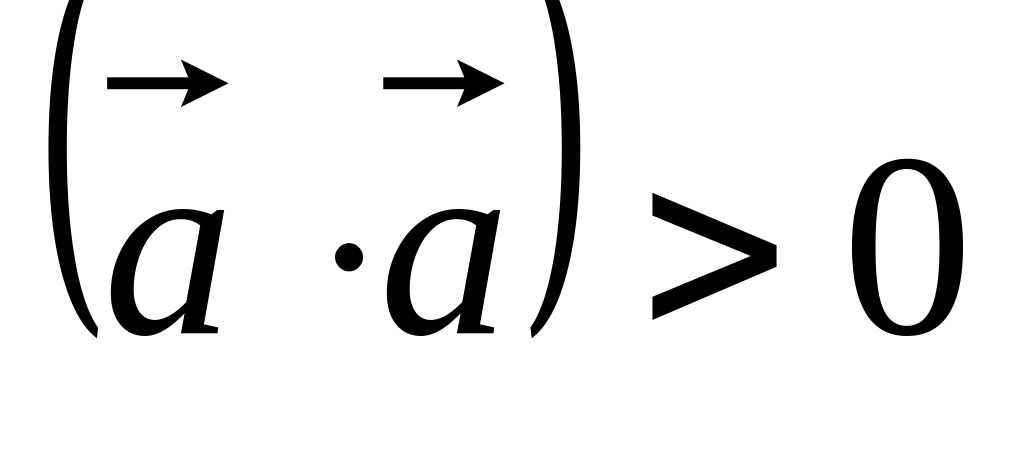 ,
если
,
иначе
,
если
,
иначе
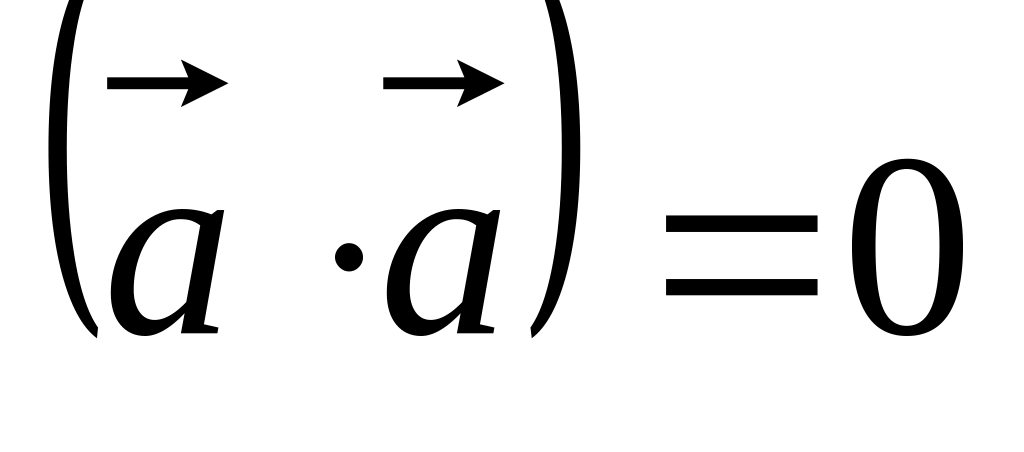 .
.Геометрические свойства скалярного произведения
С помощью скалярного произведения можно находить основные метрические величины: длины отрезков (или, что то же самое, длины векторов) и величины углов.
1. Длина вектора а
находится по формуле:
![]() .
.
2.
Величина
![]() угла
между ненулевыми векторами находится
по формуле:
угла
между ненулевыми векторами находится
по формуле:
![]() Отсюда заключаем,
что:
Отсюда заключаем,
что:
— ненулевые векторы
![]() и
и
![]() перпендикулярны
перпендикулярны
![]() тогда
и только тогда, когда их скалярное
произведение равно нулю:
тогда
и только тогда, когда их скалярное
произведение равно нулю:
![]() ;
;
— угол между
ненулевыми векторами
и
острый
![]() тогда
и только тогда, когда их скалярное
произведение положительно;
тогда
и только тогда, когда их скалярное
произведение положительно;
— угол между
ненулевыми векторами
и
тупой
![]() тогда
и только тогда, когда их скалярное
произведение отрицательно.
тогда
и только тогда, когда их скалярное
произведение отрицательно.
Алгебраическое
значение длины ортогональной проекции
вектора
на
ось, задаваемую вектором .
![]()
Ортогональная
проекция вектора
на
ось, задаваемую вектором .
![]()
Если ось задается
единичным вектором
![]() ,
то .
,
то .
![]() Свойства 1 и 2 следуют непосредственно
из определения скалярного произведения.
Третье и четвертое свойства вытекают
из геометрического смысла скалярного
произведения (см. (1.8)) и п.1 замечаний
1.4.
Свойства 1 и 2 следуют непосредственно
из определения скалярного произведения.
Третье и четвертое свойства вытекают
из геометрического смысла скалярного
произведения (см. (1.8)) и п.1 замечаний
1.4.
Необходимое и
достаточное условие ортогональности
двух векторов:
Дл
того чтобы
и
были ортогональны, необходимо и
достаточно, чтобы ![]() .
.
1.Если
или
,
то теорема справедлива, т.к. нулевой
вектор имеет произвольное направление
и
![]() .
.
Пусть . Тогда
 и, т.к.
и
и, т.к.
и
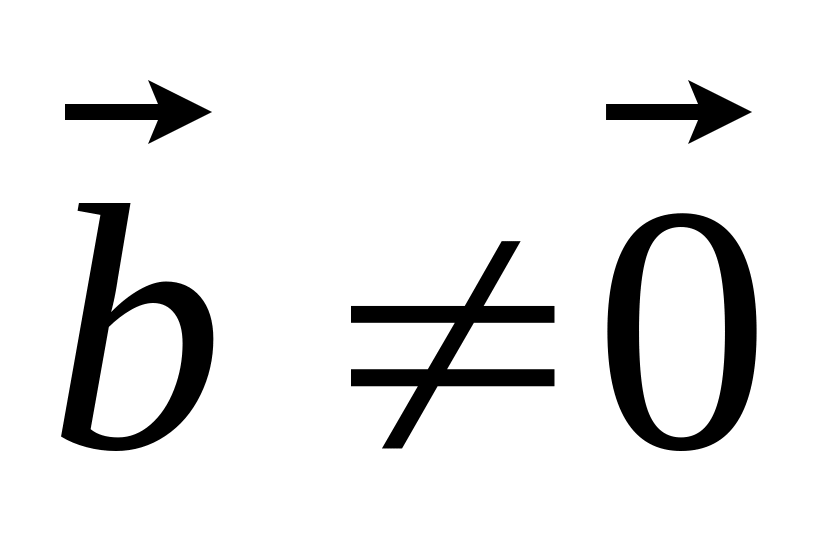 ,
то
,
то
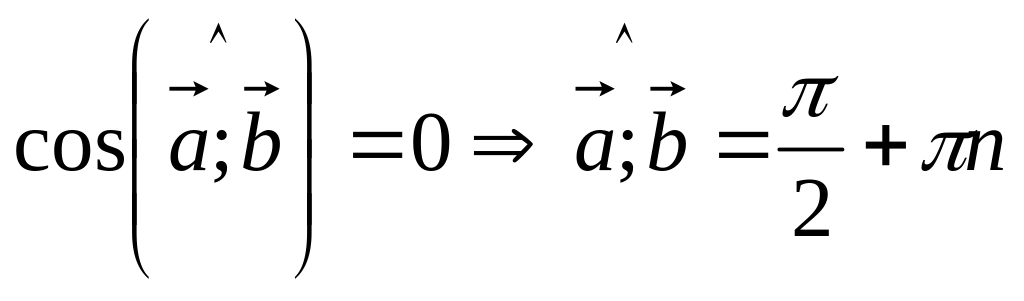 ,
т.е.
,
т.е.
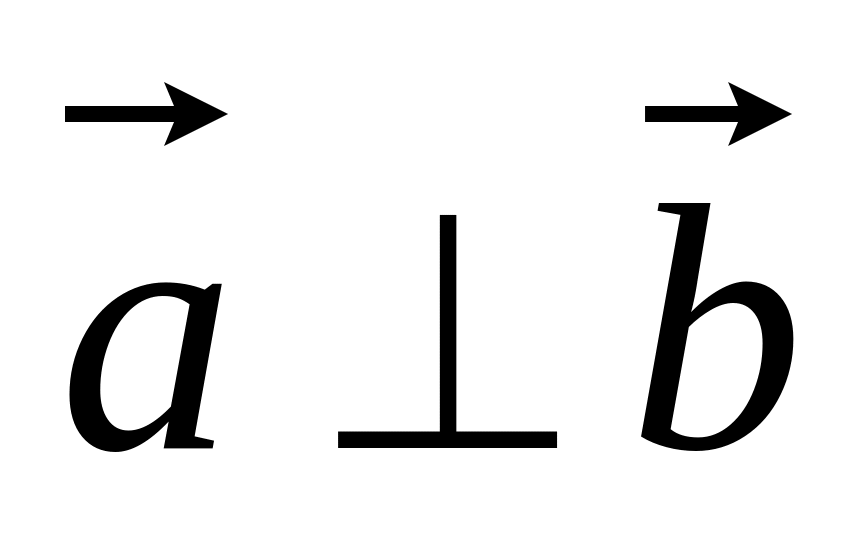 .
.Пусть . Тогда
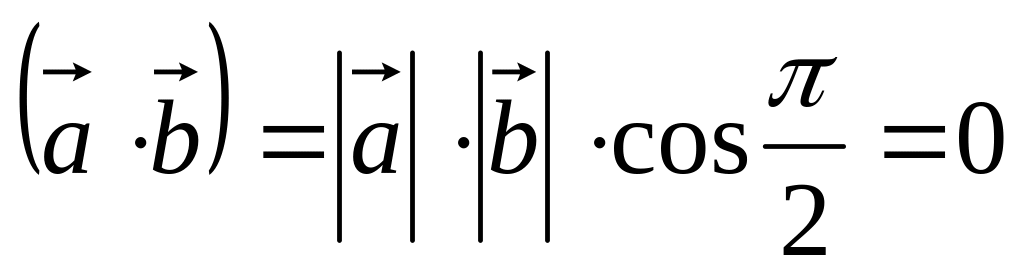 .
.
Пусть задана
прямоугольная декартова система
координат
![]() и пусть
и
.
Тогда
и пусть
и
.
Тогда
![]()
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() и
и
![]() .
.
Билет 9
Векторное произведение векторов
Три вектора называют упорядоченной тройкой векторов, если указано, какой из них первый, какой второй и какой третий.
Некомпланарная
тройка векторов
,
и
![]() называется правой (левой) если после
приведения их к общему началу
расположен по ту сторону от плоскости
векторов
и
,
откуда наикратчайший поворот от
к
кажется осуществляемым против (по)
часовой стрелки.
называется правой (левой) если после
приведения их к общему началу
расположен по ту сторону от плоскости
векторов
и
,
откуда наикратчайший поворот от
к
кажется осуществляемым против (по)
часовой стрелки.
Векторным
произведение
и
называют вектор
такой, что
![]() ,
,
![]() ,
,
![]() и векторы
,
и
образуют правую тройку. Обозначение:
и векторы
,
и
образуют правую тройку. Обозначение:
![]() .
.
Алгебраические свойства:
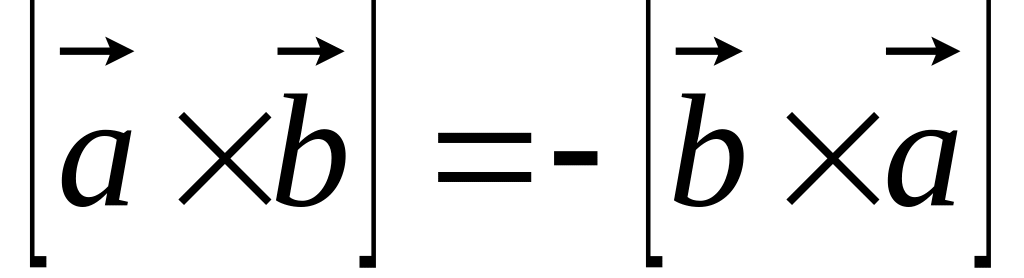 .
.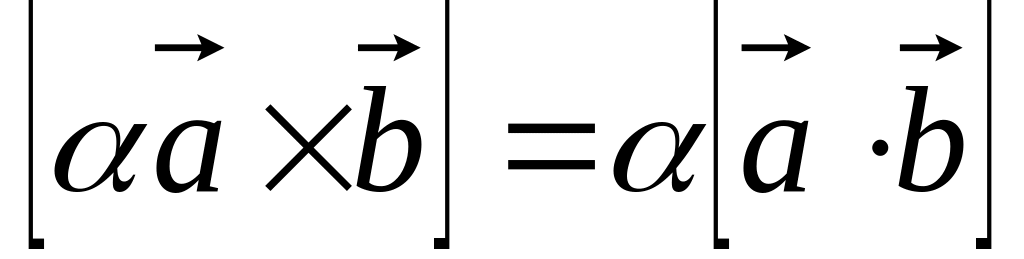 .
.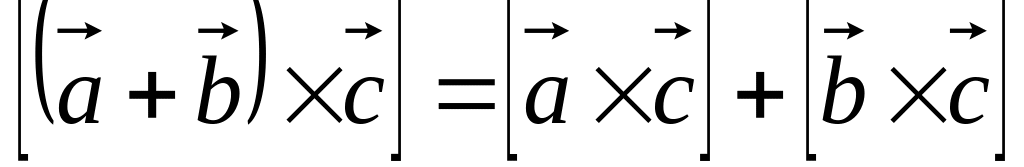 .
. .
.
Необходимое
и достаточное условие коллинеарности
двух векторов:
Для
того чтобы
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
![]() .
.
Пусть , и . Тогда
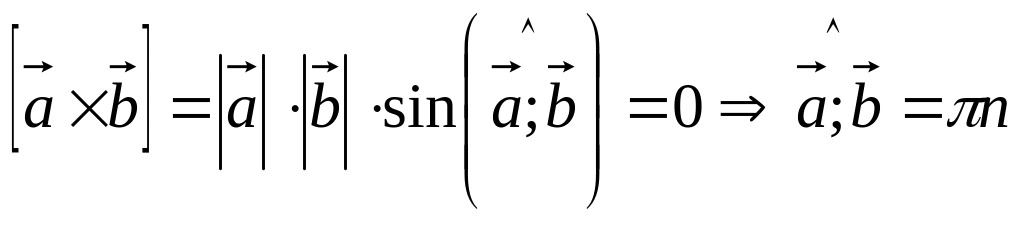 ,
т.е.
.
,
т.е.
.Пусть . Тогда
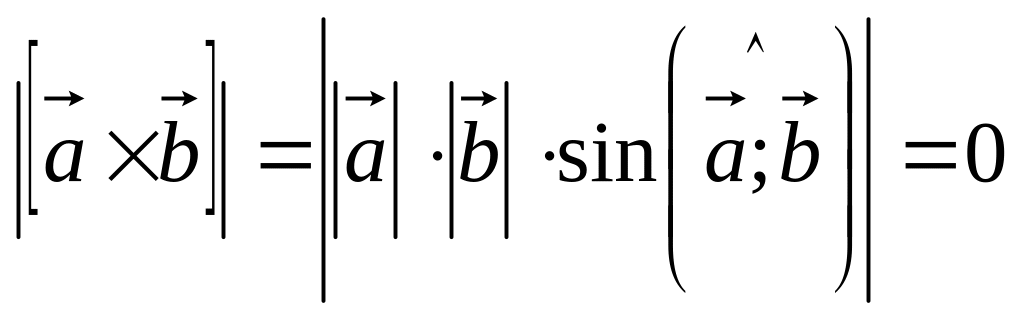 .
.
Модуль векторного произведение равен площади параллелограмма, построенного на этих векторах.
![]()
![]() .
.
Выражение векторного произведения в ДСК
Если
в ДСК
![]() и
и
![]() то
то
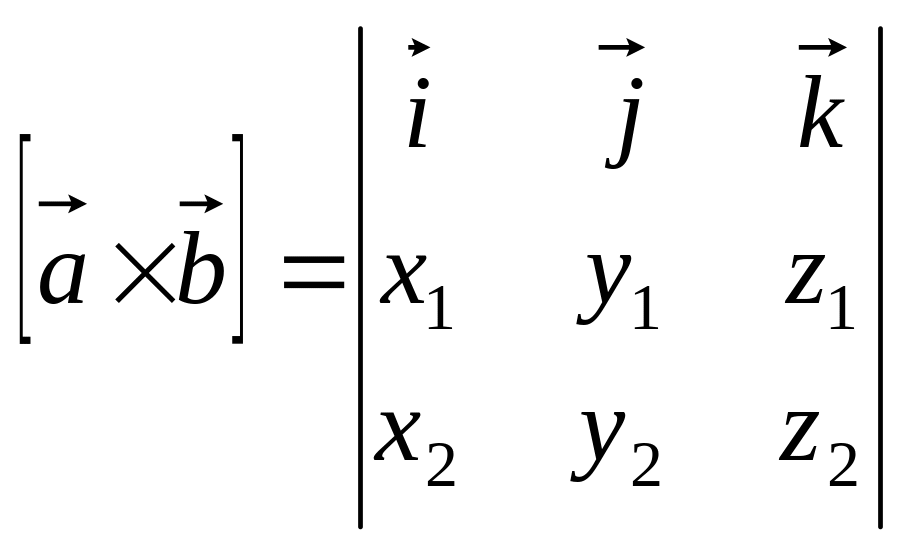 .
.
![]()
![]()
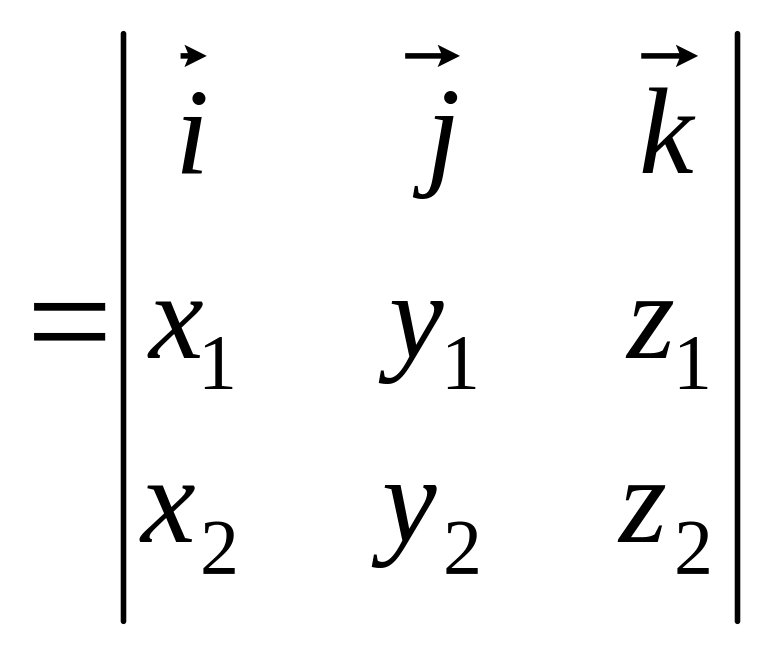 .
.
Геометрический смысл векторного произведения
1.
Необходимым и достаточным условием
коллинеарности двух векторов является
равенство нулю их векторного
произведения.
2. Длина (модуль)
векторного произведения
![]() x
x
![]() равна
площади S параллелограмма, построенного
на приведенных к общему началу векторах
и
,
т. е.
равна
площади S параллелограмма, построенного
на приведенных к общему началу векторах
и
,
т. е.
![]()
1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. 2. Длина (модуль) векторного произведения x равна площади S параллелограмма, построенного на приведенных к общему началу векторах и , т. е.
Смешанное произведение трёх векторов
Смешанным
произведением векторов
,
и
называют число
![]() .
.
М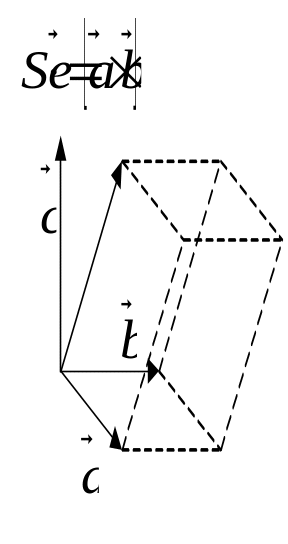 одуль
смешанного произведения векторов равен
объёму параллелепипеда, построенного
на этих векторах после приведения их к
общему началу.
одуль
смешанного произведения векторов равен
объёму параллелепипеда, построенного
на этих векторах после приведения их к
общему началу.
![]() ,
где
,
где
![]() - орт
- орт
![]() .
.
Пусть в ДСК
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
 .
.
Билет 10
Геометрические свойства смешанного произведения
1 .
Модуль смешанного произведения
некомпланарных векторов
.
Модуль смешанного произведения
некомпланарных векторов
![]() равен
объему
равен
объему
![]() параллелепипеда,
построенного на этих векторах. Произведение
параллелепипеда,
построенного на этих векторах. Произведение
![]() положительно,
если тройка векторов
—
правая, и отрицательно, если тройка
—
левая, и наоборот.
положительно,
если тройка векторов
—
правая, и отрицательно, если тройка
—
левая, и наоборот.
2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны:
![]() векторы
компланарны.
векторы
компланарны.
Докажем первое
свойство. Найдем по определению смешанное
произведение: , где
![]() —
угол между векторами
и
—
угол между векторами
и
![]() .
Модуль векторного произведения (по
геометрическому свойству 1) равен площади
.
Модуль векторного произведения (по
геометрическому свойству 1) равен площади
![]() параллелограмма,
построенного на векторах
и
параллелограмма,
построенного на векторах
и
![]() :
. Поэтому
:
. Поэтому
![]() .
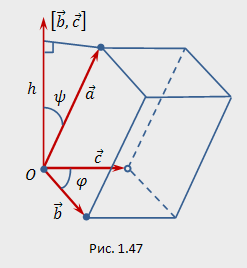
Алгебраическое значение
.
Алгебраическое значение
![]() длины
проекции вектора
на
ось, задаваемую вектором
,
равно по модулю высоте
длины
проекции вектора
на
ось, задаваемую вектором
,
равно по модулю высоте
![]() параллелепипеда,
построенного на векторах
(рис.
1.47). Поэтому модуль смешанного произведения
равен объему
параллелепипеда,
построенного на векторах
(рис.
1.47). Поэтому модуль смешанного произведения
равен объему
![]() этого
параллелепипеда:
этого
параллелепипеда:
Знак смешанного
произведения определяется знаком
косинуса угла
.
Если тройка
правая,
то
![]() и
смешанное произведение
положительно.
Если же тройка
левая,
то
и
смешанное произведение
положительно.
Если же тройка
левая,
то
![]() и
смешанное произведение
отрицательно.
и
смешанное произведение
отрицательно.
Докажем второе
свойство. Равенство возможно в трех
случаях:
![]() или
или
![]() (т.е.
(т.е.
![]() ),или
),или
![]() (т.е.
вектор
принадлежит
плоскости векторов
и
).
В каждом случае векторы
компланарны
(т.е.
вектор
принадлежит
плоскости векторов
и
).
В каждом случае векторы
компланарны
Критерий
компланарности трёх векторов:
Для
того чтобы векторы
,
и
были компланарны, необходимо и достаточно,
чтобы
![]() .
.
В самом деле, это означает, что объём параллелепипеда, построенного на этих векторах после приведения их к общему началу, будет равен нулю, а это возможно только когда все три вектора лежат в одной или параллельных плоскостях, т.е. компланарны.
Билет11
Тройно́е ве́кторное
произведе́ние
(другое название: двойное
векторное произведение)
![]() векторов
векторов
![]() —
векторное
произведение
вектора
—
векторное
произведение
вектора
![]() на
векторное произведение векторов
на
векторное произведение векторов
![]() и
и
![]()
Двойным
векторным произведением векторов
,
и
называют вектор
![]() .
.
![]() .
.
