Билет 1
Прямоугольная декартова система координат на плоскости
Прямоугольной ДСК на плоскости называют две взаимно перпендикулярные координатные оси с общим началом и одинаковой масштабной единицей. Ox – ось абсцисс, Oy – ось ординат.
Координатой
точки на плоскости называют пару чисел
x
и
y,
где
.
Записываются так:
.
Прямоугольная
система координат в пространстве
(в этом параграфе имеется в виду трехмерное
пространство, о более многомерных
пространствах — см. ниже) образуется
тремя взаимно перпендикулярными осями
координат
,
и
.
Оси координат пересекаются в точке
,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно (не обязательно[2])
одинаковы для всех осей.
—
ось
абсцисс,
—
ось
ординат,
—
ось
аппликат.
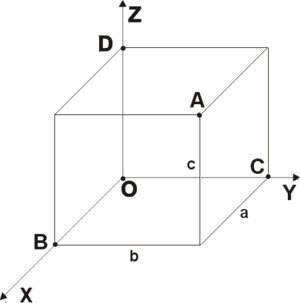
Рис.
2 Положение точки
в
пространстве определяется тремя
координатами
,
и
.
Координата
равна
длине отрезка
,
координата
—
длине отрезка
,
координата
—
длине отрезка
в
выбранных единицах измерения. Отрезки
,
и
определяются
плоскостями, проведёнными из точки
параллельно
плоскостям
,
и
соответственно.
Координата называется абсциссой точки ,
координата — ординатой точки ,
к
оордината
—
аппликатой
точки
.
Символически это
записывают так:
Или
или привязывают
запись координат к конкретной точке с
помощью индекса:
и т. п.
К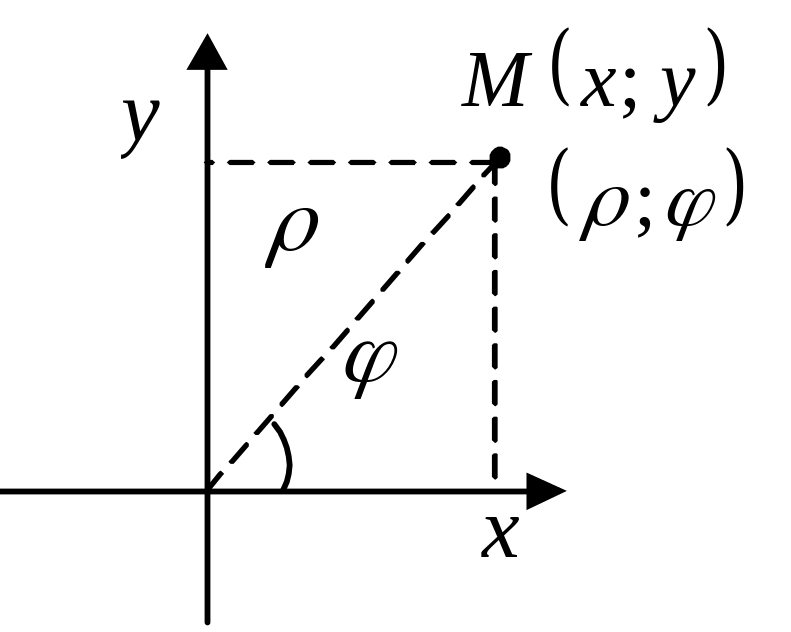
аждая
ось рассматривается как числовая
прямая,
т. е. имеет положительное направление,
а точкам, лежащим на отрицательном луче
приписываются отрицательные значения
координаты (расстояние берется со знаком
минус). То есть, если бы, например, точка
лежала
не как на рисунке — на луче
,
а на его продолжении в обратную сторону
от точки
(на
отрицательной части оси
),
то абсцисса
точки
была
бы отрицательной (минус расстоянию
).
Аналогично и для двух других осей.
Прямоугольные все системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта итп (положительное направление осей выбирают так, чтобы при повороте оси против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси , если этот поворот наблюдать со стороны положительного направления оси ).
Билет 2
П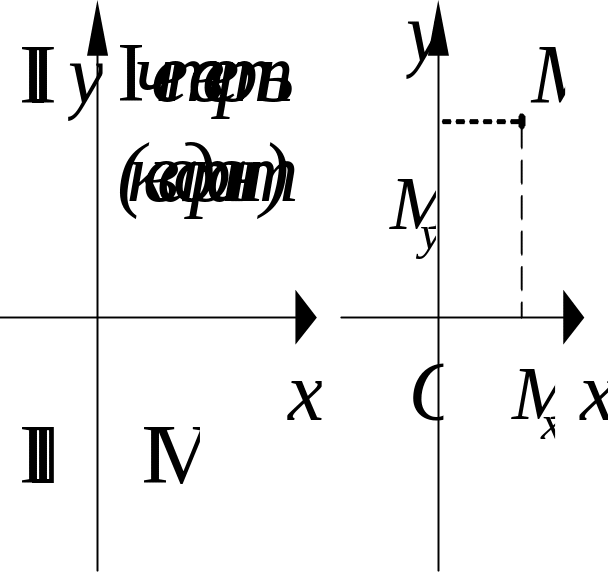
ростейшие
задачи аналитической геометрии
Пусть даны две точки
и
.
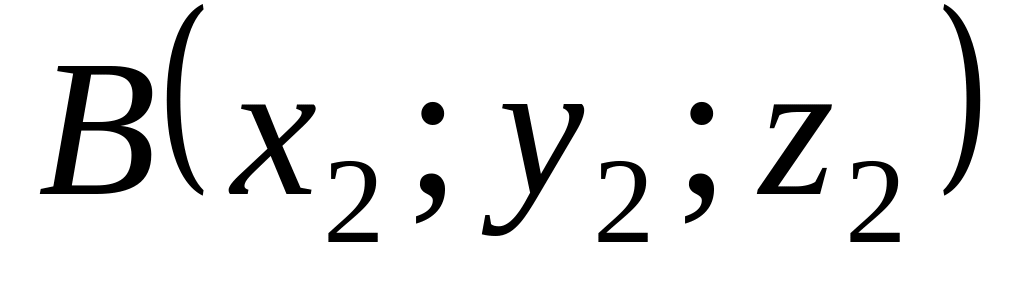Найти расстояние между ними.
Согласно теореме
Пифагора,
.
Деление отрезка в данном отношении.
Говорят, что точка C делит отрезок AB внутренним образом, если C лежит внутри AB и внешним, если C лежит вне AB.
Говорят,
что точка C
делит отрезок AB
в отношении ,
если
.
При этом, если
,
то
,
иначе
.
Замечание:
и
.
Пусть даны две
точки:
и
и пусть C
делит AB
в отношении .
Найдём точку C.
Пусть
.
Тогда по теореме Фаллеса
,
и
.
В системе из трёх материальных точек, имеющих массы m1, m2, m3 и координаты (x1, y1), (x2, y2), (x3, y3) соответственно, центр масс будет находиться на пересечении медиан (отрезков, проведённых из вершины и делящих противоположную сторону пополам) образуемого ими треугольника и иметь такие координаты (x, y): x=(m1*x1+m2*x2+x3*m3)/(m1+m2+m3); y=(m1*y1+m2*y2+x3*y3)/(m1+m2+m3)