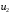Програмки с отчётами по числакам / 3. Краевая задача для ОДУ 2 порядка / 3. Вар 5
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ
Отчёт по лабораторной работе № 3
«ЧИСЛЕННОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ»
|
Программа/ Результат |
Теоретический материал |
Оценка |
|
|
|
|
Группа: Ф6-0
Курс: Численные методы
Выполнила:
Преподаватель: Рябов Павел Николаевич
Москва 2012 год
1. Полная постановка задачи:

2. График
точного решения


Для шага h=0.05
|
Точное решение задачи,
|
Численное
решение задачи с аппроксимацией
краевых условий с первым порядком
точности,
|
Численное
решение задачи с аппроксимацией
краевых условий со вторым порядком
точности,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Модуль разности точного решения и численного в первом случае,
|
Модуль разности точного решения и численного во втором случае,
|
||||||||||||||||||||||||||||||||||||||||||
|
|
Для шага h=0.1
|
Модуль
разности точного решения и численного
в первом случае,
|
Модуль
разности точного решения и численного
во втором случае,
|
||||||||||||||||||||||
|
|
Код с 1 порядком аппроксимации
//1 poryadok approximacii
uses math ;
function p(x:real):real; //pered u'
begin
p:= cosh(x);
end;
function q(x:real):real; //pered u
begin
q:= sinh(x);
end;
function f(x:real):real; //posle znaka =
begin
f:= cosh(x)+x*sinh(x) ;
end;
function y0(x:real):real; //to4noe reshenye
begin
y0:= x+exp(-sinh(x)) ;
end;
type mat=array[0..100] of real ;
var x,h:real;
n,i:integer;
f1:text;
t,x0,a,b:mat; {zadaem matricy, t - dlya koefficientov a=t[0],b=t[1],c=t[2],d=t[3]
(a,b,c - koefficienty treh diagonal'noy matricy);
x0 - dlya resheniy v tochkah;
a - dlya koefficientov A(i);
b - dlya koefficientov B(i);
chto za koefficienty? - smotret' lekcii! }
begin
assign(f1,'c:\out3-1.txt');
rewrite(f1);
h:=0.05; //shag
n:=20; // 1/h - chislo tochek
// approximaciya na levoi granice - zapicyvaem
// uravneniye a0*y(-1)+b0*y0+c0*y1=d0
t[0]:= 0.0; // a0 vsegda =0
t[1]:= 1; // b0
t[2]:= -1; // c0
t[3]:= 0.0; // d0
// Pryamoi hod
a[0]:=-t[2]/t[1]; //A(0) i B(0) pered pryamym hodom
b[0]:=t[3]/t[1];
for i:=1 to n-1 do
begin
t[0]:=(1/(h*h))-p(i*h)/(2*h);
t[1]:=-2/(h*h)+q(i*h);
t[2]:=1/(h*h)+p(i*h)/(2*h);
t[3]:=f(i*h); {ai,bi,ci,di}
a[i]:=-t[2]/(t[1]+t[0]*a[i-1]);{A(i)}
b[i]:=(t[3]-t[0]*b[i-1])/(t[1]+t[0]*a[i-1]);{B(i)}
end;
// approximaciya na pravoi granice - zapicyvaem
// uravneniye an*y(n-1)+bn*yn+cn*y(n+1)=dn
t[0]:= 1.0 ; // an
t[1]:=-1-6*h ; // bn
t[2]:= 0.0 ; // cn = 0
t[3]:=-8.376104*h; // dn
//Obratny hod
a[n]:=0; {A(n)=0! iz lekcii}
b[n]:=(t[3]-t[0]*b[n-1])/(t[1]+t[0]*a[n-1]);
x0[n]:=b[n];
for i:=n-1 downto 0 do
x0[i]:=a[i]*x0[i+1]+b[i];
// Vyvod polychennyh znacheny
writeln(f1,' y u0 y[i]-u0[i]');
writeln(f1,' ') ;
for i:=0 to n do
writeln(f1,x0[i]:1:4,' ',y0(h*i):1:6,' ',abs(x0[i]-y0(h*i)):1:6);
close(f1);
readln;
end.
Код со 2 порядком аппроксимации
//2 poryadok approximacii
uses math ;
function p(x:real):real; //pered u'
begin
p:= cosh(x);
end;
function q(x:real):real; //pered u
begin
q:= sinh(x);
end;
function f(x:real):real; //posle znaka =
begin
f:= cosh(x)+x*sinh(x) ;
end;
function y0(x:real):real; //to4noe reshenye
begin
y0:= x+exp(-sinh(x)) ;
end;
type mat=array[0..100] of real ;
var x,h:real;
n,i:integer;
f1:text;
t,x0,a,b:mat; {zadaem matricy, t - dlya koefficientov a=t[0],b=t[1],c=t[2],d=t[3]
(a,b,c - koefficienty treh diagonal'noy matricy);
x0 - dlya resheniy v tochkah;
a - dlya koefficientov A(i);
b - dlya koefficientov B(i);
chto za koefficienty? - smotret' lekcii! }
begin
assign(f1,'c:\out3-2.txt');
rewrite(f1);
h:=0.05; //shag
n:=20; // 1/h - chislo tochek
// approximaciya na levoi granice - zapicyvaem
// uravneniye a0*y(-1)+b0*y0+c0*y1=d0
t[0]:= 0.0; // a0 vsegda =0
t[1]:= 1-h*h/2*q(0); // b0
t[2]:= -1; // c0
t[3]:= -h*h/2*f(0); // d0
// Pryamoi hod
a[0]:=-t[2]/t[1]; //A(0) i B(0) pered pryamym hodom
b[0]:=t[3]/t[1];
for i:=1 to n-1 do
begin
t[0]:=(1/(h*h))-p(i*h)/(2*h);
t[1]:=-2/(h*h)+q(i*h);
t[2]:=1/(h*h)+p(i*h)/(2*h);
t[3]:=f(i*h); {ai,bi,ci,di}
a[i]:=-t[2]/(t[1]+t[0]*a[i-1]);{A(i)}
b[i]:=(t[3]-t[0]*b[i-1])/(t[1]+t[0]*a[i-1]);{B(i)}
end;
// approximaciya na pravoi granice - zapicyvaem
// uravneniye an*y(n-1)+bn*yn+cn*y(n+1)=dn
t[0]:= 1.0 ; // an
t[1]:=-1-6*h+h*h/2*(q(1)-6*p(1)) ; // bn
t[2]:= 0.0 ; // cn = 0
t[3]:=-8.376104*h+h*h/2*(f(1)-8.376104*p(1)); // dn
//Obratny hod
a[n]:=0; {A(n)=0! iz lekcii}
b[n]:=(t[3]-t[0]*b[n-1])/(t[1]+t[0]*a[n-1]);
x0[n]:=b[n];
for i:=n-1 downto 0 do
x0[i]:=a[i]*x0[i+1]+b[i];
// Vyvod polychennyh znacheny
writeln(f1,' y u0 y[i]-u0[i]');
writeln(f1,' ') ;
for i:=0 to n do
writeln(f1,x0[i]:1:4,' ',y0(h*i):1:6,' ',abs(x0[i]-y0(h*i)):1:6);
close(f1);
readln;
end.