
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ
Отчёт по лабораторной работе № 4
«ЧИСЛЕННОЕ РЕШЕНИЕ СМЕШАННОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ»
|
Программа/ Результат |
Теоретический материал |
Оценка |
|
|
|
|
Группа: Ф-0
Курс: Численные методы
Выполнил:
Преподаватель: Рябов Павел Николаевич
Москва 2012 год
1. Полная постановка задачи:



2. График
точного решения
 для различных мо-ментов времени:
для различных мо-ментов времени:

3. Результаты, полученные при выполнении лабораторной работы:
|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближённым решением в узлах сетки,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Максимальный модуль разности при t = 1.0 |
1.34e-2 |
9.19e-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Максимальный модуль разности при t = 2.0 |
3.26e-2 |
3.26e-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Максимальный модуль разности при t = 3.0 |
3.81e-2 |
7.55e-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Максимальный модуль разности при t = 5.0 |
7.23e-2 |
9.47e-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

4. График зависимости максимальной погрешности от времени:
(Синий – 1 порядок; красный – 2 порядок)

На графиках:
-
Синий – 1 порядок аппроксимации;
-
Красный – 2 порядок;
-
зелёный– точное значение.
Код с 1 порядком аппроксимации
#include<stdio.h>
#include<math.h>
#include<conio.h>
double aa=0.5, a1=1.0, b1=-1.0, a2=1.0, b2=0.0 ; //коэффициенты в уравнениях
double h=.05, tau=.05, T=5.0 ; //шаг по x и по t, T - макс. знач. времени
const int N=20 ; //количество шагов по X, равно 1/h
double f(double x, double t) {
return -sin(x+t) ;
}
double v1(double x) {
return 2.0*sin(x) ;
}
double v2(double x) {
return 2.0*cos(x) ;
}
double w1(double t) {
return 2.0*(sin(t)-cos(t)) ;
}
double w2(double t) {
return 2.0*sin(1+t) ;
}
double u0(double x, double t) {
return 2.0*sin(x+t) ;
}
int main() {
double t=0, K,L ; //K,L - константы
double xk[N+1], xk0[N+1], xk1[N+1] ;
int j ;
//Начальные условия аппрокс. до 1 порядка
for (j=0; j<=N; j++) { //рассчитываем 1 и 2 строчки вдоль X, чтобы
xk0[j]= v1(j*h) ; // запустить основной цикл
xk[j]= xk0[j] + tau*v2(j*h) ;
} xk[N]= w2(tau); //кр. условие справа I рода
t=tau ; K=aa*tau*tau/h/h; L=tau*tau ;
while (t<T) { //основной цикл - сечение функции u(x;t) в фикс. моменты времени
//t - момент времени, соответств. k-ой строке
for (j=1; j<N; j++) { // точки с x=0 и x=1 не покрываются верхушкой креста
// Основная формула для элемента u^(k+1)_j, j=1,..,N-1
xk1[j]= K*xk[j+1] + 2*(1-K)*xk[j] + K*xk[j-1] - xk0[j] + L*f(j*h,t) ; } //f считается в центре креста
t += tau ; //t - время на k+1 слое
// Краевые условия аппроксимированы до 1 порядка
xk1[0]= (xk1[1]+h*w1(t))/(1.0+h) ;
xk1[N]= w2(t) ;
for (j=0; j<=N; j++) {
xk0[j]= xk[j] ;
xk[j]= xk1[j] ;
}
}
FILE *file ;
file = fopen("c:/4.txt", "w");
printf(" x y(x) u0 |y-u0| \n") ;
fprintf(file," x y(x) u0 |y-u0| \n") ;
for (j=0; j<=N; j++) { //значения по X в конечный момент времени
printf("%.2f %.6f %.6f %.2e\n", j*h, xk1[j], u0(j*h,t), abs(xk1[j]-u0(j*h,t)) ) ;
fprintf(file,"%.2f %.6f %.6f %.2e\n", j*h, xk1[j], u0(j*h,t), abs(xk1[j]-u0(j*h,t)) ) ;
}
fclose(file) ;
getch();
return 0;
}
Код со 2 порядком аппроксимации
/* Шаблон - крест, явная схема. */
#include<stdio.h>
#include<math.h>
#include<conio.h>
double aa=0.5, a0=1.0, b0=-1.0, a1=1.0, b1=0.0 ; //коэффициенты в уравнениях
double h=.05, tau=.05, T=5.0 ; //шаг по x и по t, T - макс. знач. времени
const int N= 20 ; //количество шагов по X, равно 1/h
double f(double x, double t) {
return -sin(x+t) ;
}
double v1(double x) {
return 2.0*sin(x) ;
}
double v2(double x) {
return 2.0*cos(x) ;
}
double w0(double t) {
return 2.0*(sin(t)-cos(t)) ;
}
double w1(double t) {
return 2.0*sin(1+t) ;
}
double u0(double x, double t) {
return 2.0*sin(x+t) ;
}
double p2v1(double x) { //Вторая производная u(x;0)
return -2.0*sin(x) ;
}
int main() {
double t=0, C,L ; //C,L - константы
double xk[N+1], xk0[N+1], xk1[N+1] ;
int j ;
//Начальное условие аппрокс. до 2 порядка
for (j=0; j<=N; j++) { //рассчитываем 1 и 2 строчки вдоль X, чтобы
xk0[j]= v1(j*h) ; // запустить основной цикл
xk[j]= xk0[j] + tau*v2(j*h) + tau*tau/2.0*(aa*p2v1(j*h)+f(j*h,0));
} xk[N]= w1(tau);//кр. условие справа I рода
t= tau ; C= aa*tau*tau/h/h; L= tau*tau ;
while (t<T) { //основной цикл - сечение функции u(x;t) в фикс. моменты времени
//t - момент времени, соответств. k-ой строке
for (j=1; j<N; j++) { // точки с x=0 и x=1 не покрываются верхушкой креста
// Основная формула для элемента u^(k+1)_j, j=1,..,N-1
xk1[j]= C*xk[j+1] + 2*(1-C)*xk[j] + C*xk[j-1] - xk0[j] + L*f(j*h,t) ; } //f считается в центре креста
t += tau ; //время на (k+1) слое
// Краевые условия аппроксимированы до 2 порядка
xk1[0]= tau*tau/h/h*(xk[1]-(1.0+h)*xk[0])+tau*tau/h*w0(t-tau)+2.0*xk[0]-xk0[0]+tau*tau*f(0,t-tau);
// 2.0*(1.0+C*(a0/b0*h-1.0))*xk[0]-xk0[0]+2.0*C*xk[1]+L*f(0,t)-2.0*C*h/b0*w0(t);
xk1[N]= w1(t) ;
for (j=0; j<=N; j++) {
xk0[j]= xk[j] ;
xk[j]= xk1[j] ;
}
}
FILE *file ;
file = fopen("c:/4.txt", "w");
printf(" x y(x) u0 |y-u0| \n") ;
fprintf(file," x y(x) u0 |y-u0| \n") ;
for (j=0; j<=N; j++) { //значения по X в конечный момент времени
printf("%.2f %.6f %.6f %.2e\n", j*h, xk1[j], u0(j*h,t), abs(xk1[j]-u0(j*h,t)) ) ;
fprintf(file,"%.2f %.6f %.6f %.2e\n", j*h, xk1[j], u0(j*h,t), abs(xk1[j]-u0(j*h,t)) ) ;
}
fclose(file);
getch();
return 0;
}


 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени
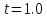



 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени




 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени




 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени


