
Програмки с отчётами по числакам / 4. Волновое уравнение. Шаблон-крест / 4. Вар 13
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ
Отчёт по лабораторной работе № 4
«ЧИСЛЕННОЕ РЕШЕНИЕ СМЕШАННОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ»
|
Программа/ Результат |
Теоретический материал |
Оценка |
|
|
|
|
Группа: Ф6-0
Курс: Численные методы
Выполнил:
Преподаватель: Рябов Павел Николаевич
Москва 2012 год
1. Полная постановка задачи:



2. График
точного решения
 для различных моментов времени
для различных моментов времени
 :
:
3. Результаты, полученные при выполнении лабораторной работы:
|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближённым решением в узлах сетки,
|
||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
||
|
|
Максимальный модуль разности при t = 0.5 |
.e- |
.e- |
||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
||
|
|
Максимальный модуль разности при t = 1.0 |
.e- |
.e- |
||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
||
|
|
Максимальный модуль разности при t = 1.5 |
.e- |
.e- |
||||

|
Узлы пространственной сетки,
|
Численное
решение
|
Точное решение задачи в узлах сетки,
|
Модуль разности между точным и приближенным решением в узлах сетки,
|
||||
|
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
Аппроксимация 1 порядка |
Аппроксимация 2 порядка |
||||
|
0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
|
|
|
|
|
||
|
|
Максимальный модуль разности при t = 2.0 |
.e- |
.e- |
||||

4. Полулогарифмический график зависимости максимальной погрешности от времени:

Код с 1 и 2 порядком аппроксимации начальных и граничных условий, шаблон-крест
uses crt, math;
Function f(x,t:real):real;
begin
f:=(1+cos(t-x)+x*sin(t-x)/2)/power(1+cos(t-x),2);
end;
Function phi1(x:real):real;
begin
phi1:=x*(1-sin(x/2)/cos(x/2));
end;
Function dphi1(x:real):real;
begin
dphi1:=-(2*cos(x/2)+x*sin(x/2))/2/power(cos(x/2),3) ;
end;
Function phi2(x:real):real;
begin
phi2:=1+x/(1+cos(x)) ;
end;
Function psi1(t:real):real;
begin
psi1:=1+sin(t/2)/cos(t/2) ;
end;
Function psi2(t:real):real;
begin
psi2:=t+1/(1+cos(t-1)) ;
end;
Function U0(x,t:real):real;
var arg:real;
begin
arg:=(t-x)/2;
U0:=t+x+x*sin(arg)/cos(arg) ;
end;
var
j,k,nx,nt:integer;
hx,ht,xmax,tmax,aa,sr,m:real;
x,t:array[0..500] of real;
u1,u2: array [0..500,0..500] of real;
Output:text;
begin
clrscr;
Assign(output,'c:/4.txt');
Rewrite(output);
aa:=1/2;
hx:=0.05;
ht:=0.05;
xmax:=1;
Write('T max = '); Readln(tmax);
nx:=round(xmax/hx);
nt:=round(tmax/ht);
x[0]:=0;
t[0]:=0;
For j:=1 to nx do
x[j]:=x[j-1]+hx;
For k:=1 to nt do
t[k]:=t[k-1]+ht;
{1 poryadok approks.}
For j:=0 to nx do
begin
U1[j,0]:=phi1(x[j]);
U1[j,1]:=U1[j,0]+ht*phi2(x[j]);
end;
For k:=1 to nt-1 do
begin
For j:=1 to nx-1 do
U1[j,k+1]:=2*U1[j,k]-U1[j,k-1]+aa*ht*ht/(hx*hx)*(U1[j+1,k]-2*U1[j,k]+U1[j-1,k])+f(x[j],t[k])*ht*ht;
U1[0,k+1]:=(U1[1,k+1]-hx*psi1(t[k+1])) ;
U1[nx,k+1]:=(U1[nx-1,k+1]-hx*psi2(t[k+1])) / (1-hx);
end;
{2 poryadok approks.}
For j:=0 to nx do
begin
U2[j,0]:=phi1(x[j]);
U2[j,1]:=phi1(x[j])+ht*phi2(x[j])+ht*ht/2*(aa*dphi1(x[j])+f(x[j],0));
end;
For k:=1 to nt-1 do
begin
For j:=1 to nx-1 do
U2[j,k+1]:=2*U2[j,k]-U2[j,k-1]+aa*ht*ht/(hx*hx)*(U2[j+1,k]-2*U2[j,k]+U2[j-1,k])+f(x[j],t[k])*ht*ht;
U2[0,k+1]:=2*aa*ht*ht/(hx*hx)*(U2[1,k]-U2[0,k]-hx*psi1(t[k]))+2*U2[0,k]-U2[0,k-1]+ht*ht*f(0,t[k]);
U2[nx,k+1]:=2*aa*ht*ht/(hx*hx)*(U2[nx-1,k]-(1-hx)*U2[nx,k]-hx*psi2(t[k]))+2*U2[nx,k]-U2[nx,k-1]+ht*ht*f(x[nx],t[k]);
end;
k:=nt;
Writeln(output,'T= ',t[k]);
Writeln(output,'Tochnoe reshenie');
For j:=0 to nx do
Writeln(output,U0(x[j],t[k]));
Writeln(output);
Writeln(output,'Shislennoe 1-go poryadka');
For j:=0 to nx do
Writeln(output,U1[j,k]);
Writeln(output);
Writeln(output,'Raznost 1-go poryadka s tochnim');
For j:=0 to nx do
Writeln(output,abs(u1[j,k]-U0(x[j],t[k])));
Writeln(output);
Writeln(output,'Shislennoe 2-go poryadka');
For j:=0 to nx do
Writeln(output,U2[j,k]);
Writeln(output);
Writeln(output,'Raznost 2-go poryadka s tochnim');
For j:=0 to nx do
Writeln(output,abs(u2[j,k]-U0(x[j],t[k])));
Writeln(output);
Writeln(output,'-------');
Writeln(output);
{1}
Writeln(output,'maximaln. modul raznosti dlya 1-go poryadka');
k:=nt;
m:=0;
For j:=0 to nx do
begin
sr:=abs(u1[j,k]-U0(x[j],t[k]));
If m<sr
then m:=sr;
end;
Writeln(output,m);
{2}
Writeln(output,'maximaln. modul raznosti dlya 2-go poryadka');
k:=nt;
m:=0;
For j:=0 to nx do
begin
sr:=abs(u2[j,k]-U0(x[j],t[k])) ;
If m<sr
then m:=sr;
end;
Writeln(output,m);
Close(output);
Readln;
end.


 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени




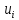 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени




 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени




 задачи в узлах сетки в момент времени
задачи в узлах сетки в момент времени


