13) Метод Гаусса розв’язання систем лінійних алгебраїчних рівнянь.

Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь.

Початок алгоритму.

Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду.

З цього моменту починається зворотний хід.

З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок.

Приклад

Запишемо розширену матрицю системи

14) Однорідні системи лінійних алгебраїчних рівнянь. Загальний і частинний розв’язки. Загальний і частинний розв’язки

Система лінійних рівнянь називається однорідною, якщо праві частини цих рівнянь дорівнюють нулю:

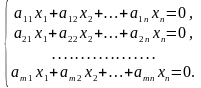
Така система завжди сумісна, тому що розширена матриця відрізняється від основної на стовпець, який являє собою нуль-вектор. Оскільки система, яка має нуль-вектор завжди лінійно залежна, то ранг розширеної матриці збігається з рангом основної. Це очевидно, тому що система завжди має тривіальний розв’язок:

x₁= x₂= x₃= … = x_n=0.

Запишемо систему у векторній формі:

і доведемо, що сукупність розв’язків системи утворює підпростір. Для цього треба довести, що коли вектори

є розв’язком системи, то i також будуть розв’язками цієї системи.

Дійсно, за умовою

Додавши ці рівності, дістанемо

Помноживши рівняння (6.15) на λ знайдемо

Це означає, що та також є розв’язками системи .

Нехай матриця

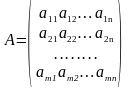
має ранг r, тобто серед векторів є r лінійно незалежних, причому . Тоді система векторів

де j=r+1, r+2, …, n лінійно залежна:

Покладемо = – , тоді

Розв’язками цього рівняння є вектори

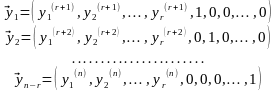
при цьому число координат у векторів дорівнює n.

Доведемо, що вектори лінійно незалежні. Дійсно, якщо рівність

записати в скалярній формі, то вона виконується лише за умови

Доведемо, що будь-який розв’язок однорідної системи , є лінійною комбінацією векторів , тобто

Припустимо, що рівність не виконується, тобто

Знайдемо координати вектора :

Оскільки вектори і є розв’язками системи, то і вектор є розв’язком цієї системи:

Через те що , останні доданків дорівнюють нулю. Тоді

Оскільки вектори лінійно незалежні, остання рівність можлива лише при

тобто , доведено.

Таким чином, вектори утворюють базис підпростору розмірності .

Сукупність розв’язків однорідної системи утворює підпростір розмірності . Число рівнянь m збігається з розмірністю підпростору, в якому задано вектори. У цьому просторі максимальне число лінійно незалежних векторів може бути не більше m, ранг r≤m, а число невідомих n. Тобто система має нетривіальний розв’язок, якщо число невідомих більше числа рівнянь: n-m>0 . Якщо ж число рівнянь m збігається з рангом матриці і дорівнює числу невідомих, то однорідна система має єдиний тривіальний (нульовий) розв’язок. Те саме спостерігаємо, коли в однорідній системі число рівнянь буде більше числа невідомих. Такі розв’язки називаються загальними розв’язками однорідної системи. Сукупність лінійно незалежних розв’язків системи називається фундаментальною системою розв’язків. Змінні називаються вільними, – базисними.