7. Обратная матрица.

Ответ:

Единичная матрица – матрица, включающая 1 по главной диагонали и 0 в остальных местах.

Обратная матрица: матрица А-1 будет обратной для матрицы А, если А-1 • А = Е.

Теорема: для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е.

А ≡  ≠ 0.

Формула обратной матрицы:

- А • Х = В;

- A*A^-1*Х=В*А^-1

- Х = В*А^-1

- А^-1=1/det*A^T

Алгоритм нахождения обратной матрицы.

1. Находим определитель исходной матрицы ( если det =0 => существует матрица обратная данной)

2. Находим алгебраические дополнения элементов.

3. Формируем полученную матрицу.

4. Транспонируем данную матрицу ( т.е. меняем строки и столбцы новой полученной матрицы)

5. Находим по формуле описанной выше.

8. Системы линейных уравнений, основные понятия. Запись системы линейных уравнений в матричной форме.

Ответ:

Решение системы линейных уравнений – совокупность из n чисел xik, которые обращают ее в верные равенства.

Решить систему – выяснить совместна она или нет.

Совместная система – система алгебраических уравнений, имеющая хотя бы одно решение.

Определенная система – совместная система, имеющая единственное решение.

Неопределенная система – совместная система, имеющая более одного решения.

Эквивалентные системы – системы, имеющее одно и тоже общее решение.

Матричная запись:

А • Х = В;

9.Формулы Крамера решения системы n-линейных с n неизвестными.

Ответ:

Для системы линейных уравнений с неизвестными (над произвольным полем)

Пример.

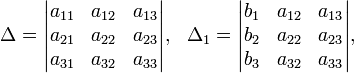
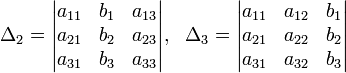
Искомые корни будут решением для данной системы.

10.Решение системы n-линейных уравнений с n-неизвестными с помощью обратной матрицы.

Посмотреть в вопросе 6, и применить на практике ( это практический вопрос)

11.Метод Гаусса системы n-линейных уравнений с n – неизвестными.

(Практический вопрос посмотреть в учебнике и применить на практике)

12.Метод Гаусса решения системы m- линейных уравнений с n – неизвестными (m<n)

Аналогично 11 вопросу применить на практике.

13.Теорема Кронекера-Капелли, формулировка

Ответ:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора

Пример:

Определить совместность системы линейных уравнений:

RgA=2

A* = RgA* = 3.

Исходя из формулировки следует, что система несовместна.