§18.Моменты сопротивления сечения.

Осевым моментом сечения называется отношение осевого момента инерции к максимальному расстоянию от центра тяжести сечения до наиболее удаленной точки противоположной оси.

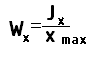
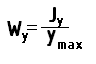
Полярным моментом сопротивления сечению называется отношение полярного момента инерции к максимальному полярному радиусу сечения.

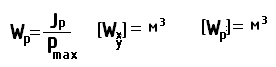
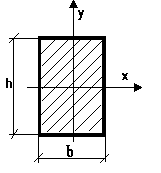
а) Для прямоугольного сечения

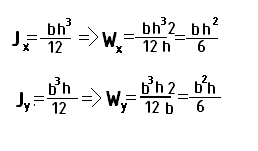
б) Для круглого сечения:

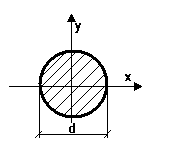
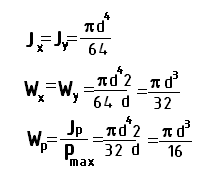
в) Для кольцевого сечения:

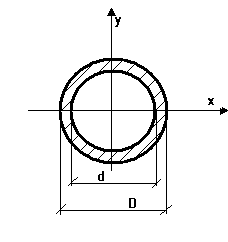
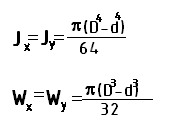
§19.Кручение.

Кручение – такой вид нагружения бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор, отличный от нуля, называемый крутящий момент.

М_кр или М_z

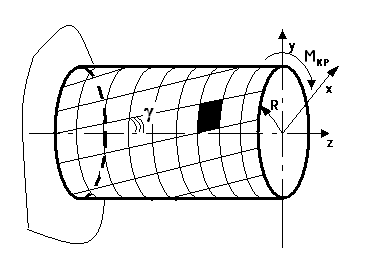
Пример конструкции, работающей на кручение – вал.

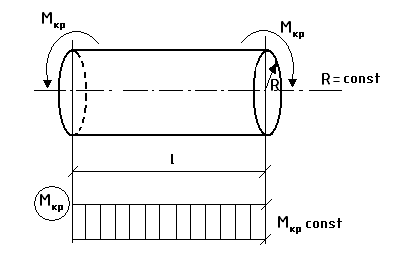
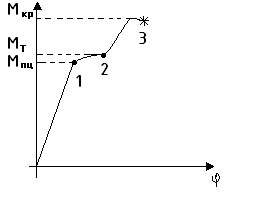
φ – угол кручения

Закон Гука для кручения.

τ =σ*γ

- до деформации;

- после деформации.

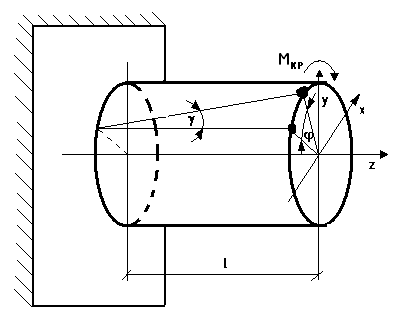
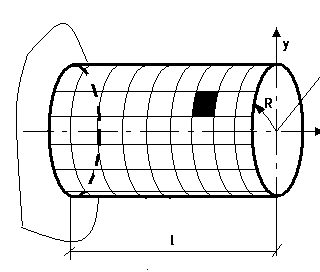
Опыт показывает, что расстояние между скручиваемыми волокнами вала не изменяется, продольные линии сетки приобретают винтовые формы, винтовые углы сетки искажаются как в случае сдвига.

Следствия:

выделяемый элементарный объем материала находится в условиях чистого сдвига, радиусы остаются прямыми и неизменной длины.

Нижележащие слои (глубжележащие (ближе к центру)) испытывают меньшую деформацию, а максимума деформация достигает по образующей поверхности цилиндра (R – max).

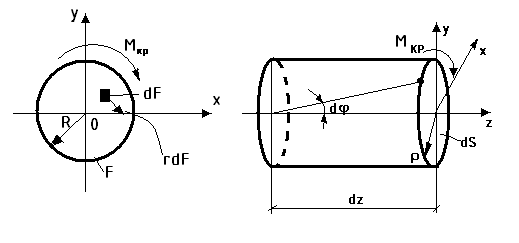
dS=ρ*dφ

γ~tgγ=dS/dz

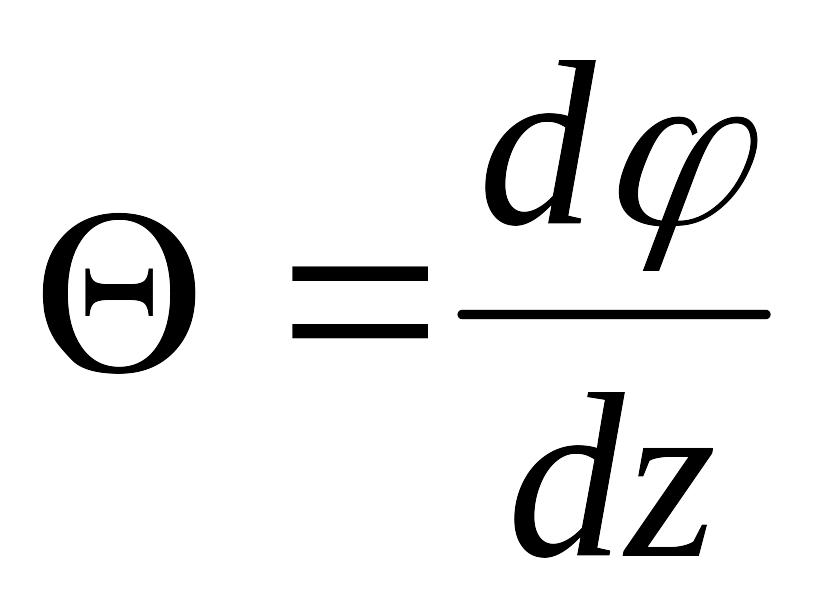
- относительный угол закручивания

G – модуль сдвига

, - жесткость при кручении

[G J_P]= =H*M²

G_стали=0,8 МПа (Е_стали=2*10⁵МПа)

G<E (всегда)

формула для определения касательных напряжений при кручении

§20.Расчеты на прочность и жесткость при кручении.

Расчеты на прочность	Расчеты на жесткость
1. Проверочный расчет
Условие прочности	Условие жесткости
%- погрешность
а) определение d вала
б) определение крутящего момента

§21. Сдвиг и смятие.

Смятие – такой вид деформации бруса, при которой в любом его поперечном сечении возникает только поперечная сила.

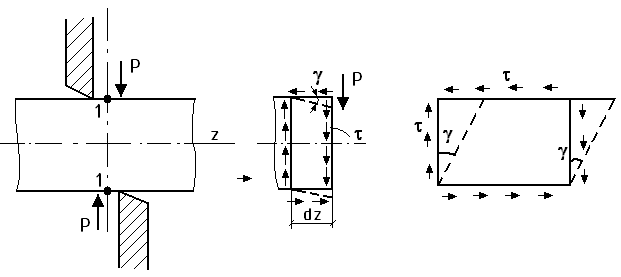
При изгибе возникают только касательные напряжения, они всегда парные.