Температурные напряжения.

R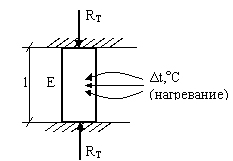 _T – температурная реакция, возникающая в заделках.

ε = αΔt

α – температурный коэффициент линейного расширения материалов

Δl_t = αΔtl

Согласно формуле Гука

При нагреве температура реакции заделки - отрицательна, при охлаждении – положительна.

Монтажные (начальные) напряжения

Монтажными напряжениями – напряжения, возникающие вследствие неточности изготовления элементов конструкции.

Пример

С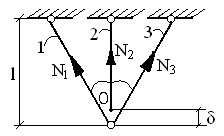 тержень 2 короче проектировочной длины на величину S.

δ<<l

В результате стяжки всех трех стержней в точке О, стержни 1 и 3 - укоротятся, а стержень 2 – удлинится.

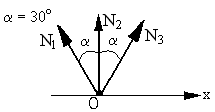
1. Основные уравнения равновесия:

∑F:(x) = −N₁ sinα + N₃ sinα = 0

N₁ = N₃ (1)

∑F:(x) = −N₁ cosα + N₂ + N₃ cosα = 0

N₂ = −2N₁ cosα (2)

3 неизвестных – 2 основных уравнения равновесия =1раз статически неопределимая система.

2. Дополнительное уравнение перемещений:

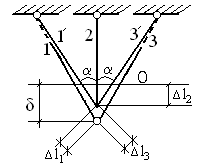
α – const

Δl₁= ( δ–Δl₂) cosα (3)

3)

l ₂ = l

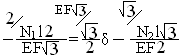
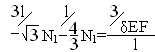
§8. Механические свойства материалов.

Основными механическими характеристиками являются :

• прочность;

• пластичность;

• упругость;

• твёрдость.

• Прочностью называется способность конструкции сопротивляться воздействию внешних сил, не разрушаясь.

• Пластичность – способность материала давать значительные остаточные деформации, не разрушаясь.

• Упругость – способность материала восстановлять первоначальные формы и размеры после снятия нагрузки или температуры.

• Твёрдость – способность материала сопротивляться проникновению в него другого тела практически не получающего остаточной деформации.

Механические характеристики металлов необходимы для проведения инженерных расчетов и определяются экспериментально путем испытания стандартных образцов на растяжение – сжатие, кручение, изгиб, срез, смятие и т.д.

Для металлов проводят испытание на растяжение.

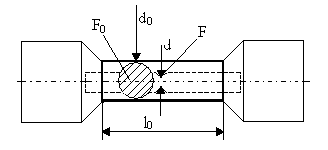
l₀ – первоначальная длина рабочей части образца;

d₀ – первоначальный диаметр рабочей части образца.

При растяжении испытательная машина фиксирует величину растягивающего усилия P и величину Δl (абсолютное удлинение).

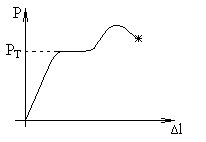
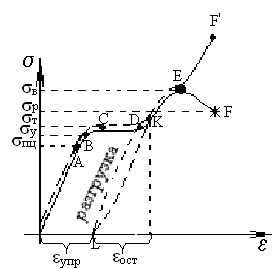
Первичная диаграмма растяжения малоуглеродистой стали.

σ =Ρ/F₀

ε = Δl/l

σ_пц – предел пропорциональности;

σ_у – предел упругости;

σ_т – предел текучести;

σ_в – предел прочности (временное сопротивление);

σ_р – напряжение в момент разрыва.

ОА – участок прямой пропорциональности между σ и ε (область действия закона Гука σ = Eε).

σ_пц – то наибольшее напряжение, для которого выполняется закон Гука.

σ_пц = P_пц/ F₀

B – точка, соответствующая пределу упругости(σ_у).

На отрезке АВ деформация не подчиняется линейному закону, но обратимы.

σ_у = P_у/ F₀

С – начало площадке текучести;

D – конец площадке текучести;

CD – площадка текучести.

σ_Т = P_Т/ F₀

После точки В все деформации необратимы. При постоянном значение силы P_Т наблюдается заметный рост деформации – материал течет.

DE – зона упрочнения (положительный криволинейный участок).

Прямая параллельна участку ОА.

Петля KLK – петля гистерезиса.

ε = ε_уп + ε_ост

Если произвести полную разгрузку, а затем снова нагрузить образец, то он покажет более высокие значения предела пропорциональности, предела упругости, предела текучести, предела прочности.

Явление полной разгрузки, а потом нагрузки с целью повышения прочностных характеристик материалов называется наклепом или наготовкой. Явление наклепа используется в технике для повышения прочностных свойств материала например изготовление цепей, грузоподъемных машин. Если наклеп нежелателен, то его устраняют отжигом.

Точка Е соответствует временному сопротивлению – наибольшее напряжение, которое может выдержать образец до разрушения.

σ_B = P_max/ F₀

Точка F – точка разрушения образца.

EF – зона местной текучести, образование “шейки”.

При образовании шейки площадь поперечного сечения образца резко уменьшается. При этом заметно падает сила P (показано экспериментально).

σ_P = P_P/ F₀ или σ_P = P_P/ F_шейки

(условное напряжение в момент разрыва)

(истинное напряжение в момент разрыва)

I.Условная диаграмма растяжения обозначена прямой

линией (───).

II.Истинная диаграмма растяжения обозначена пунктирной

линией(-----)

Характеристики прочности материала являются

σ_Т и σ_B.

Характеристики пластичности материала являются

σ = (l₀ - l_К/ l₀) * 100% - относительное удлинение

ψ = F₀ - F_ш / F₀ * 100% - относительное сужение

Многие материалы не имеют ярко выраженной площадки текучести.

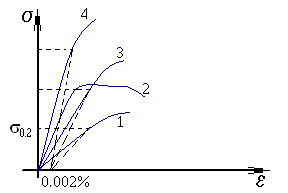
1 – кривая растяжения бронзы;

2 - кривая растяжения малоуглеродистойстой стали (В Ст3);

3 - кривая растяжения никелевой стали;

4 - кривая растяжения марганцовистой стали.

σ_0,2 – условной предел текучести определяется для материалов, не имеющих ярко выражений, площадь текучести соответствует напряжению, при котором остаточная деформация 0,2% от первоначальной длины образца.

ГОСТ 1497 – 84 - на σ_0,2

Хрупкость понятие обратное пластичности – способность материала разрушаться без образования заметных деформаций (остаточных).

Примеры:

-хрупкие материалы: бетон, чугун, стекло, природный камень;

-пластичные материалы: сталь, медь, бронза, алюминий, сплав.

Пластичные материалы испытываются на растяжение.

Хрупкие материалы – на сжатие.

При испытании на сжатие хрупкие материалы разрушаются без образования площадки текучести.

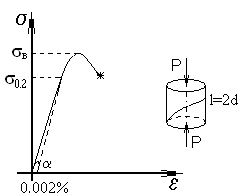
Диаграмма сжатия чугунного образца.

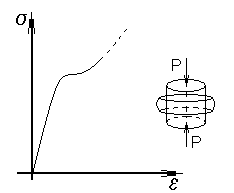
Диаграмма сжатия стального образца.

Твердость. Определение твердости материалов является косвенным методом определения предела прочности. Для определения твердости материала в него с определенной силой вдавливается другое тело (индентор) и по полученному отпечатку судят о твердости материала.

1. Твердость по Бринеллю: индентор – закаленный стальной шарик.

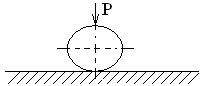
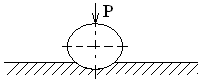
Где D – диаметр шарика;

d – диаметр отпечатка.

2. Твердость по Виккерсу: индентор – алмазная четырехгранная пирамида с углом 136 между гранями.

Где F – площадь отпечатка;

b - полусумма диагонали отпечатка.

3. Твердость Роквеллу: индентор – алмазный конус с углом 120 при вершине.

Применяются (по Роквеллу и Виккерсу), когда твердость по Бриннелю НВ > 4 000 МРа.

4. Разрушение образцов с помощью маятникового направления.

По высоте отскока бойка копра при ударе от образца судят о энергии, затраченной на его разрушение.