Д

Угловые

γ_xy; γ_yz;γ_xz

еформированное состояние точки тела полностью определяется

6-ю компонентами деформации:

Линейные

ε_x; ε_y; ε_z

Перемещения являются абсолютными величинами, выражаемыми в единицах длины или в радианах.

Деформации - относительные величины, выражаемые в процентах (безразмерные).

§6. Центральное растяжение - сжатие. Закон Гука.

Центральное рстяжение-сжатие – такой вид деформации бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор отличный от 0 – нормальная (продольная) сила N, приложенная в центре тяжести поперечного сечения груза.

Если N действует от сечения, то она вызывает растяжение (увеличение длины) и считается положительной.

Если N действует к сечению, то она вызывает сжатие (укорочение бруса) и считается отрицательной.

N>0 – растяжение

N<0 – сжатие

Брусья, в основном работающие на растяжение-сжатие называются стержнями.

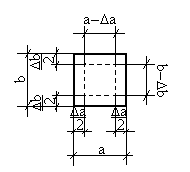
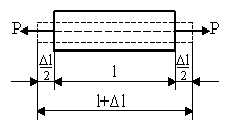
Экспериментально доказано:

П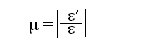 ри центральном растяжении–сжатии отношение поперечной деформации к продольной величине постоянно для данного материала и её абсолютное значение называется коэффицентом Пуассона.

0 ≤ μ ≤ 0,5 (в зависимости от пластичности)

Пример:

μ _пробки=0

μ_чугуна =0,23÷0,27

μ_стали =0,29÷0,33

μ_меди =0,31÷0,33

μ_{каучука}=0,47

Для большинства материалов с достаточной точностью можно сказать:

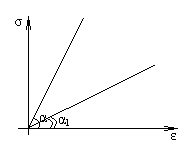
В упругой области нагружения существует прямо пропорциональная зависимость между относительной линейной деформацией и нормальным напряжением, называемым законом Гука (1756г. – Роберт Гук).

σ = Εε

где ε – относительная линейная деформация

σ – напряжение

Ε – модуль упругости первого рода (модуль Юнга)

[Н/м²]; [Па]; [МПа]

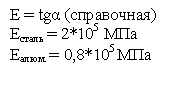
E F – жесткость при растяжении-сжатии

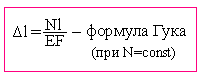
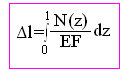
Пример:

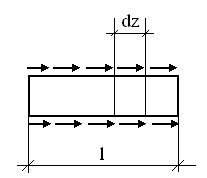
Определить удлинение стержня, вызываемое действием собственного веса. (δ=? Δl=?)

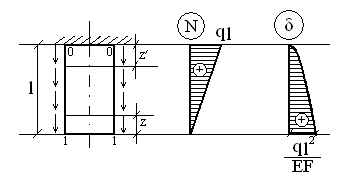
0 ≤ z ≤ l 0 ≤ z′ ≤ l

N(z) = qz N(z′) = ql-qz′

N(0) = 0 N(0) = ql

N(l) = ql N(l) = 0

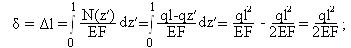
Ответ:

Примечание: Если стержень состоит из n различных участков, то Δl (суммарная) определяется как сумма:

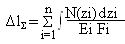
§7. Потенциальная энергия упругой деформации при растяжении – сжатии.

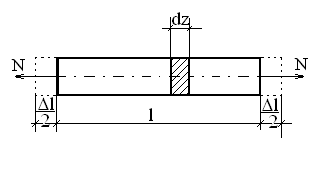
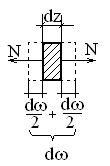
EF – жесткость при растяжении – сжатии;

F – площадь поперечного сечения.

Статические неопределимые системы.

Статической неопределимыми системами называются системы, в которых внутренние силовые факторы не могут быть определены из основных уравнений равновесий (число неизвестных больше числа основных уравнений статики).

Степень статической неопределимости – разность между числом неизвестных (в опорах или заделках) и число уравнений равновесия.

Для раскрытия статической неопределимости составляют дополнительные уравнения перемещений (совместимости деформации). Их число равно степени статической неопределимости системы.

3 стороны задачи:

1. Статическая;

2. Геометрическая;

3. Физическая.

Пример

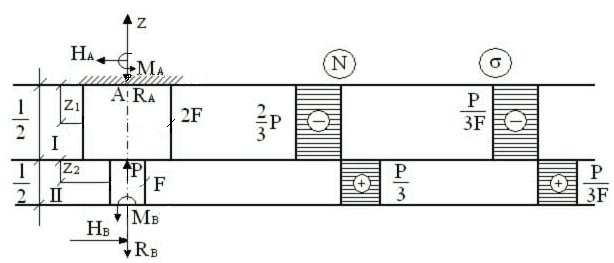
H_B = 0, H_A= 0,

M_A = 0, M_B= 0,

Статическая сторона задачи:

1. Основное уравнение равновесия (уравнение статики)

∑Fi(z) = -R_A+ P+ R_B = 0

2 неизвестных – 1 уравнение равновесия = 1 раз статической неопределимой системы.

Геометрическая сторона задачи:

2. Дополнительное уравнение перемещения (уравнение совместимости деформации)

Δl_I + Δl_II = 0

Физическая сторона задачи:

( 3б) в (1)