§30. Линейное напряженное состояние.
Линейное напряженное состояние возникает при центральном и/или внецентринном растяжении – сжатии, при чистом и косом изгибе.
-
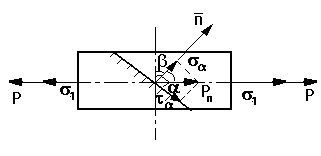нормаль к наклонной площадке
-вектор
полного нормального напряжения;
-
нормальное напряжение;
-
касательное напряжение.
а)
-
- напряжение, действующее на главную
площадку.
б).
-
главная
площадка.
в).
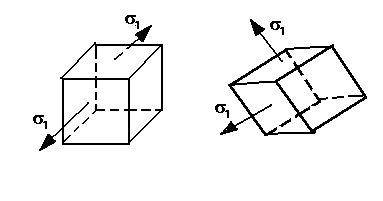
Максимальные касательные напряжения возникают на наклонных площадках с углом 450.
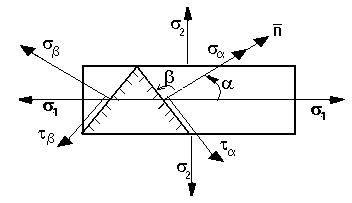
§31. Плоское (двухосное) напряженное состояние.
Плоское напряженное состояние возникает при поперечном изгибе, кручении в элементах тонкостенных оболочек, нагруженных внешним или внутренним давлением.
1)
2)
3)
1)
2)
3)
4)
5)
Экстремальные значения напряжения.
А)
;
Б)
;
В)
Площадки, по которым касательные напряжения достигают экстремальных значений, называются площадками сдвига.
Рассмотрим, как определяются главные напряжения при заданных нормальных и касательных.
Д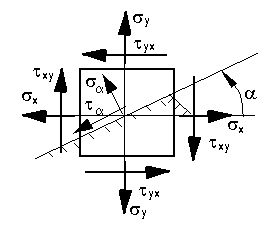
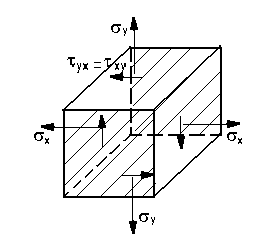ано:
Найти:
-
(двухосное напряженное состояние)
Уравнение
вида:
Формула для определения двух главных напряжений при одном известном.
§32. Полное напряжение на наклонной площадке.
Направления
главных площадок находим из уравнения
т.е.
-
угол наклона главных площадок от
направления
против хода часовой стрелки
§33. Круги Мора при плоском напряженном состоянии.
В теории напряженных состояний различают 2 задачи:
1).по известным в точках главным площадкам и главным направлениям определить нормальные и касательные напряжения, действующие на наклонных плоскостях.
2).обратная задача: по известным нормальным и касательным напряжениям на наклонных площадках требуется найти главные площадки и главные напряжения, а также угол наклона α.
Графическое решение обеих задач осуществляется при помощи построения кругов Мора.
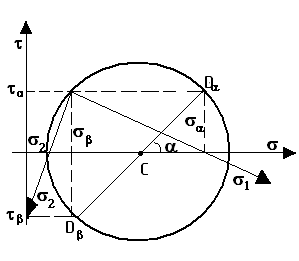
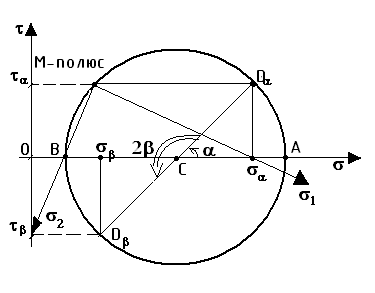
Дано σ1,σ2,α Найти:σα,τα σβ,τβ
§34. Объемное трехосное напряженное состояние.
Объемное напряженное состояние возникает при совместном действии:
изгиба и растяжения-сжатия;
кручения и растяжения – сжатия;
наружном и внутреннем давлении в сосуде.
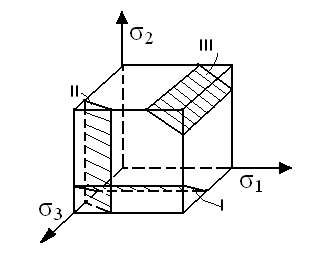
σ1, σ2, σ3≠0
σ1≥ σ2≥ σ3
В площади I нормальные и касательные напряжения не будут зависеть от главного напряжения σ1, а будут зависеть от σ2, σ3.
Нарисуем круги Мора для трехосного напряженного состояния
-
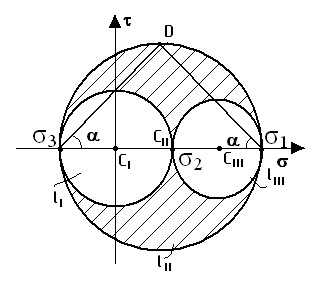
всегда будет лежать в заштрихованной
области.
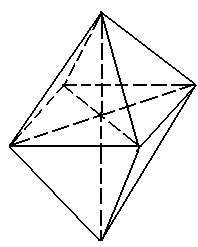
Угол наклона октоэдрической площадки σ1σ2σ3=45о.
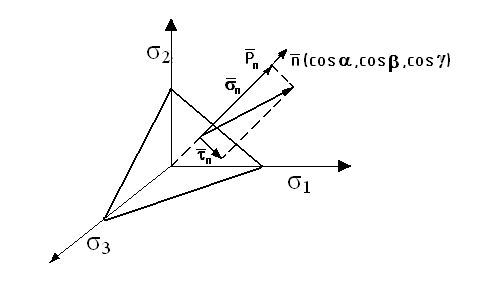
