VIII. Сложное сопротивление. §38. Понятие сложного сопротивления. Принцип суперпозиции.

Понятие сложное сопротивление означает, что в поперечном сечении бруса под действием его силы возникает более одного внутреннего силового фактора. (простое сопротивление – один силовой фактор).

Простое сопротивление	Сложное сопротивление
1.Растяжение – сжатие (N)	1.Поперечный изгиб (Qy,Mx или Qx,My)
2.Кручение (Mz)	2.Внецентренное растяжение-сжатие (N, Mx, My)
3.Чистый изгиб (Mx или My)	3.Косой изгиб (Mx, My)
	4.Изгиб + кручение (Mизг, Mкр)
	5.Изгиб + растяжение-сжатие (Mизг+N)
	6.Растяжение-сжатие+кручение (N,Mz)

Принцип суперпозиции (принцип независимости действия сил) означает, что результирующее напряжение в случае сложного сопротивления определяется как сумма напряжений от каждого внутреннего силового фактора в отдельности.

Понятие сложного сопротивления не эквивалентно по смыслу понятию сложного напряженного состоянию (одно не подразумевает другое).

а ) внецентренное растяжение-сжатие

_x=0; _y=0;

_xy=0;

_yz=0;

_zx=0;

₁=_z;

₂=0;₃=0

Одноосное напряженное состояние, но сложное сопротивление, т.к. 3 внутренних силовых фактора;

б) кручение

_x=0; _y=0;_z=0

_max = _xz;

_min = -_xz;

_  _xz;

₂ = 0;

₃  -_xz

§39. Косой изгиб.

Изгиб называется косым, если плоскость действия возникающим изгибающим моментом , возникающая в поперечном сечении бруса неперпендикулярно ни одной из главных центральных осей сечения.

Плоский косой изгиб	Пространственный косой изгиб
При плоском изгибе упругое линия бруса – это плоская кривая.	При пространственном косом изгибе нагрузки, вызывающие его действуют в разных силовых (продольных) плоскостей. При пространственном косом изгибе упругая линия бруса – это пространственная кривая.

Разложение косого изгиба на две составляющие

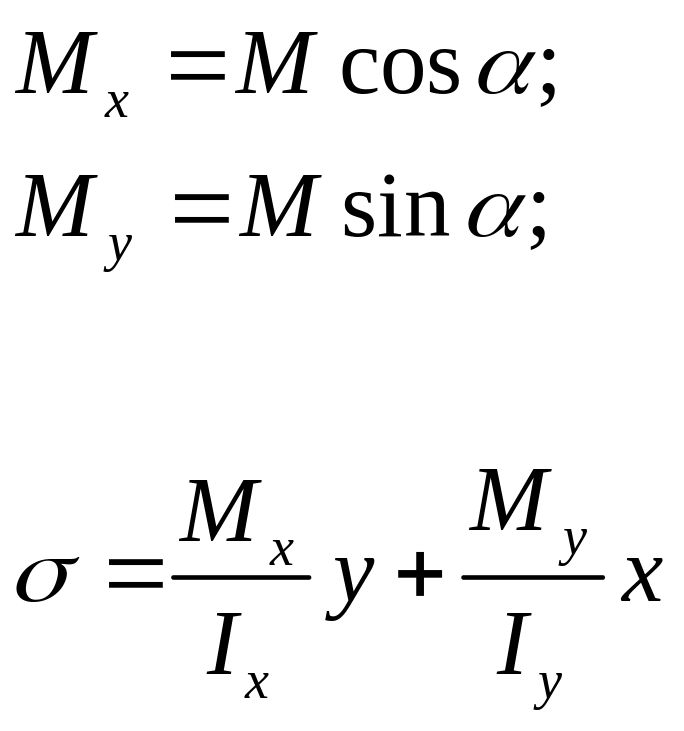
Ф-ла для определения напряжения при косом изгибе.

Координаты x,y принадлежат любой точке поперечного сечения бруса и при определении напряжения следует учитывать их знак.

Приравняем данное уравнение к 0 и получим из него уравнение нейтральной линии.

- уравнение нейтральной линии

Данная зависимость показывает, что нейтральная линия неперпендиеклярно следу силовой плоскости от момента M.

- справедливо относится к несимметричному сечению.

В случае симметричного сечения относительно обоих осей (x,y) =>

Нейтральная линия перпендикулярно следу силовой плоскости от момента M.

В точках A и B от действия момента M (возникает максимальное напряжение), тогда условие прочности имеет вид: