3. Бездиафрагменные коробчатые пролетные строения с замкнутым деформируемым поперечным сечением (рис.19.5).

Помимо изгиба, свободного и стесненного кручения поперечные сечения испытывают деформации контура.

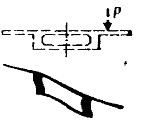
Рис.19.5. Пролетное строение с тонкостенным деформируемым контуром поперечного сечения

Расчет этих пролетных строений на кручение производится в два этапа. На первом этапе определяются усилия в соответствии с теорией тонкостенных стержней с замкнутым недеформируемым контуром, а на втором этапе учитывают влияние деформаций контура по нижеприведенной схеме.(рис.6)

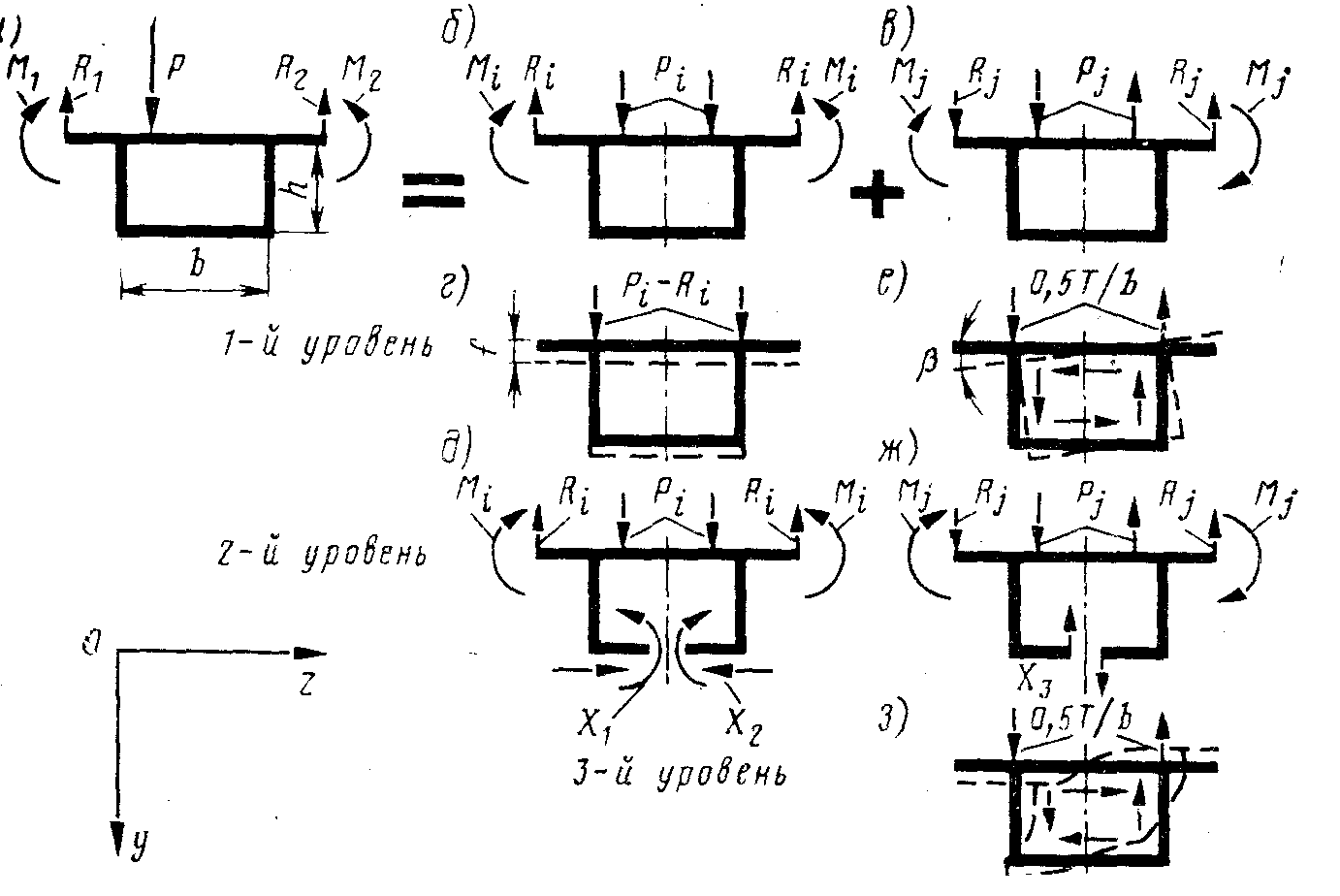
Рис.19.6.Схемы к расчету сечений коробчатых балок.

В соответствии с этой схемой напряженное состояние поперечного сечения пролетного строения с заданной нагрузкой Р (рис.19.6 а) представляется в виде суммы напряженных состояний того же сечения с симметричным (рис. б) и кососимметричным (рис. в) воздействием. При этом сечение по схеме19.6, б) будет работать только на изгиб, а сечение по схеме19.6,в) только на кручение.

Далее на первом уровне симметрично загруженная балка рассматривается с недеформируемым контуром поперечного сечения (рис.19.6, г). При этом определяются изгибающие моменты M_z и поперечные силы Q_y., воспринимаемые полным сечением балки, а по ним напряжения _x и _xy. На втором уровне учитывают местный поперечный изгиб элементов сечения от внеузлового приложения нагрузки при несмещающихся узлах контура. Для замкнутой поперечной рамы задача может быть решена методом сил с лишними неизвестнымиХ₁ и Х₂ в середине нижней плиты рамы (рис.19.6,д) с получением нормальных _x и касательных _yz напряжений в верхней плите, а также напряжений _y в стенках балки.

Для несимметрично загруженной балки можно рассмотреть три уровня расчета. На первом уровне рассматривается кручение балки с недеформируемым контуром поперечного сечения ( рис.19.6, е) замкнутого профиля. На втором уровне вычисляются изгибные напряжения в элементах контура, а на третьем касательные напряжения. При расчете несимметрично загруженной балки на внеузловую нагрузку методом сил с одним лишним неизвестнымХ₃ (рис. ж) используются формулы приведенные в книге М.Е. Гибшмана и В.И. Попова

При таком подходе от действия полного внешнего крутящего момента в сечениях коробчатой балки возникают внутренние бимоменты B_ и соответствующие им нормальные напряжения стесненного кручения _, моменты свободного кручения M_i, вызывающие касательные напряжения _i и изгибно-крутящие моменты M_ с касательными напряжениями от стесненного кручения _.

При этом должны быть вычислены дополнительные геометрические характеристики сечения: I_ - главный секториальный момент инерции сечения; S_- главный секториальный статический момент инерции сечения.

Тогда в общем случае загружения балки осевой силой с изгибом и кручением полное выражение для нормальных и касательных напряжений будет иметь следующий вид

где - главная секториальная координата точки, в которой вычисляется напряжение.

3. Пролетные строения, представляющие собой сочетание балок и плит- цилиндрические складчатые оболочки. К ним относятся бездиафрагменные ребристые и многокоробчатые пролетные строения соединенные плитой проезжей части.(рис.19.7)

Рис.19.7. Деформации поперечных сечений пролетных строений в виде цилиндрических складчатых оболочек.

Для расчета пролетных строений этой группы требуется использовать наиболее сложные методы расчета. Наибольшее применение нашел метод плитно – балочных конструкций, разработанный Улицким Б.Е. с учениками. В соответствии с этим методом пролет­ное строение расчленяют продольными разрезами на от­дельные плиты и балки (стенки).

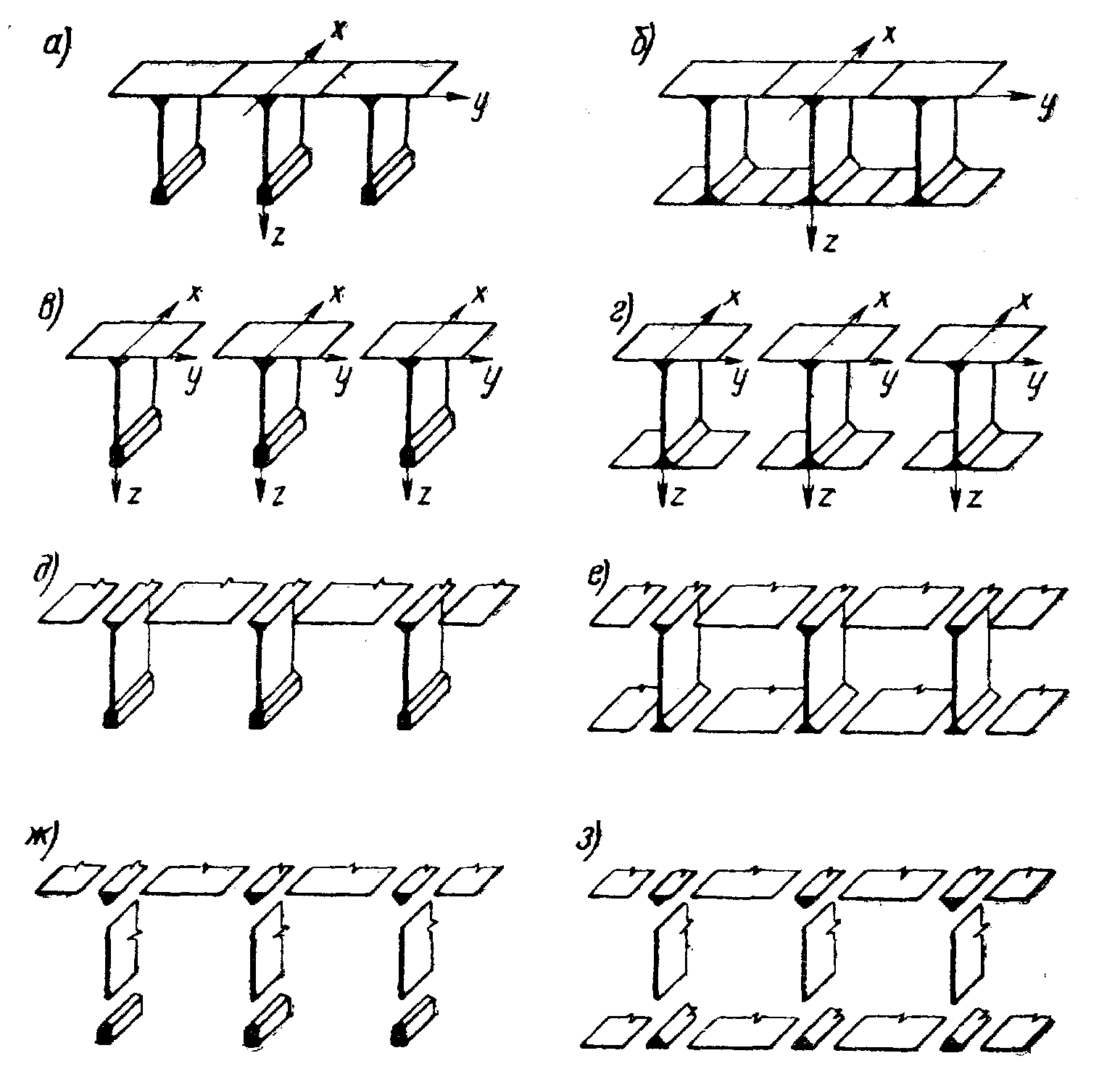
Рис. 19.8. Схемы членения плитно-балочных пролетных строений

В зависимости от стоящих перед расчетчиками задач, слож­ности и требуемой точности расчета рекомендуется применять следующие схемы членения:

а) на тавровые, двутавровые или другого .сечения балки (рис. 19.8, в, г);

б) на балки и горизонтальные плиты (рис. 19.8, д, е,)\

в) на стержни, вертикальные и горизонтальные плиты (рис. 19.8,ж, з),

В случаях когда требуется детально рассчитать плиту проез­жей части, рекомендуется схема, изображенная на рис19.8, д, е; когда необходимо рассчитать главные балки на кручение и опре­делить возникающие в их стенках поперечные изгибающие мо­менты — схема, представленная на рис. 8, ж, з; в расчетах слож­ных конструкций и систем мостов используют схему, изображенную на рис.19. 8,0, г.

Взаимодействие между собой отдельных продольных элемен­том, их деформации и возникающие между ними внутренние уси­лия можно определить исходя из положений метода сил, метода перемещений или смешанного метода. Лишние неизвестные в зависимости от их особенностей могут быть выражены в виде функций или дискретных величия.

В методе сил лишними неизвестными являются силы и моменты в сечениях между смежными элементами. На единице длины сечения учитывают четыре компонента сил и мо­ментов (рис.19. 9),

В плоскостях разрезов вводят неизвестные непрерывно изменяющиеся вдоль координаты х нормаль­ные N(x) , поперечные Q(x), сдвигающие усилия T(x), а также изгибающие моменты M(x). Характер изменения неизвестных вдоль разрезов зависит от внешней нагрузки и характеристик пролетного строения.

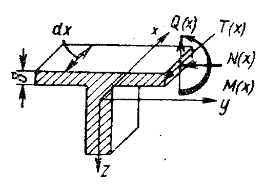
Рис.19.9. Компоненты лишних неизвестных в методе сил

Эти силы и моменты являются функциями абсциссы х, направленной вдоль пролета и принимающей на его концах значения 0 и L. Их выражают в форме тригонометриче­ских рядов:

(А)

Все внешние нагрузки также представляют в тригонометрических рядах с использованием известных формул для коэффициентов разложения различных нагрузок в ряд Фурье.

Для определения неизвестных составляют кано­нические уравнения метода сил, характеризующие условия совместно­сти деформаций плит и балок. В общем виде для каждого продольного сечения составляется четыре уравнения, характеризующие.:

1. совместность продольных перемещений U вдоль оси x;

2. совместность поперечных перемещений V вдоль оси y;

3. совместность поперечных перемещений W вдоль оси z;

4. совместность поворотов Ф относительно продольной оси x.

Эти уравнения могут быть записаны в виде (В)

(В)

В этих уравнениях учитываются суммарные перемещения (линейныеV, U, W и угловые Ф) от воздействия всех неизвестных N, T, Q, M и внешней нагрузки q.

Уравнения (В) составляют для каж­дого разреза, причем деформации плитных элементов определяют мето­дами теории упругости как для пластинок, а деформации балочных элементов методами сопротивления материалов как для упругих брусьев. При решении системы (В) линейных уравнений определяют постоянные коэффициенты для всех сечений, после чего по формулам (А) находятся со­ответствующие величины усилий. Зная величины внутренних и внешних усилий, приложенных к каждому элементу, можно вычислить деформации и напряжения, действующие в каждом из них.

Метод плитно-балочных конструкций отличается высокой точно­стью получаемых результатов, однако он требует проведения громоздких вычислений и применяется только в сочетании с ПК.

К недостаткам метода можно отнести также сложность учета переменности сечений по длине пролетов и граничных условий в сложных системах

Для расчета пролетных строений группы 5 в последнее время широ­кое применение находит метод конечных элементов. Эффективность ме­тода связана с возможностью наиболее просто учитывать различные краевые условия, особенности прикладываемых нагрузок, форму рассчитываемых конструкций и т. д. При этом конструкции расчленяется на некоторое число эле­ментов конечных размеров, деформированное состояние которых яв­ляется простым.