3. Диафрагменные ребристые или коробчатые пролетные строения с недеформируемым контуром поперечного сечения, составленного из тонкостенных стержней.

Тонкостенным называют стержень, составленный из пластинок, отношение высоты или ширины которых к их толщине не менее 7-8, а длина стержня значительно превышает контуры поперечного сечения. При работе такого пролетного строения под воздействием нагрузок контуры его поперечного сечения не деформируются благодаря наличию диафрагм по его длине. Особенностью этих пролетных строений является то, что в их поперечных сечениях возникают напряжения не только от изгиба и свободного кручения, но и от стесненного кручения, создающегося вследствие наличия диафрагм.

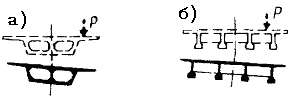
Рис.19.4.Пролетные строения с тонкостенным недеформируемым контуром поперечного сечения.

Изгиб этих пролетных строений рассчитывается с помощью уравнения (1).

Для расчета кручения таких ребристых пролетных строений, которые являются тонкостенными стержнями с открытым контуром поперечного сечения, используется теория В.З. Власова, дающая следующее дифференциальное уравнение стесненного кручения 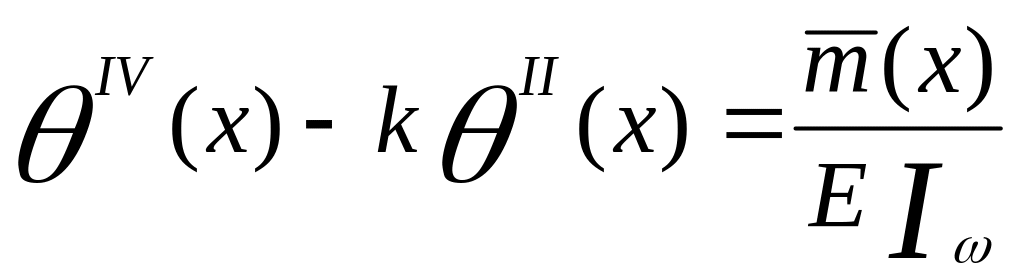(5)

(5)

где θ(х)- угол закручивания стержня;

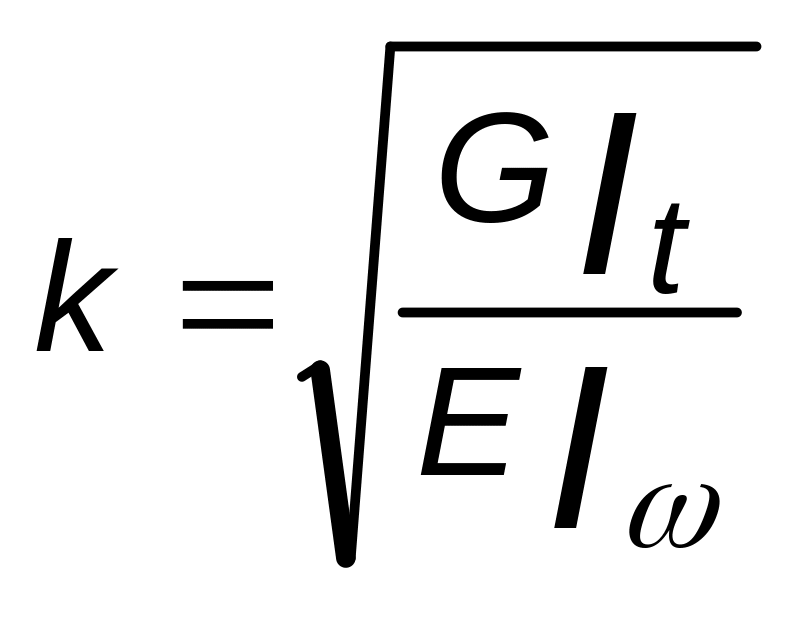- изгибно-крутильная характеристика сечения, зависящая от модулей сдвига G и упругости E, момента инерции на кручение I_t и секториального момента инерции сечения ;

m(x) – интенсивность внешней закручивающей нагрузки.

Для расчета кручения тонкостенных стержней с замкнутым контуром поперечного сечения используется теория тонкостенных стержней замкнутого профиля, разработанная А.А. Уманским. Основное дифференциальное уравнение (6), полученное им из условий равновесия, отличается от уравнения В.З. Власова дополнительным членом в правой части

(6)

где 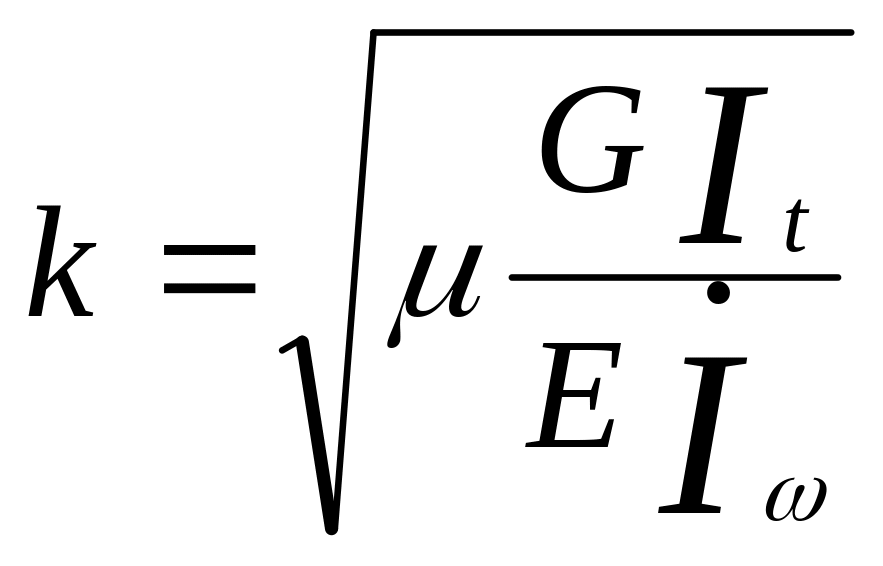-изгибно-крутильная характеристика сечения, отличающаяся от соответствующей характеристики в уравнении В.З. Власова коэффициентом депланации μ;

μ = 1- I_t / I_p –коэффициент депланации сечения;I_t- момент инерции сечения при кручении; I_{p -} полярный момент инерции; I_ω- главный секториальный момент инерции сечения.

Решение уравнений (5) и (6) находится в виде суммы общего решения однородного уравнения, получаемого при равенстве нулю правой части, и частного решения, учитывающего действие внешней нагрузки, соответствующей правой части. При решении однородного уравнения используется метод начальных параметров, в качестве которых принимается: начальный угол закручивания и мера депланации сечения, бимомент и полный крутящий момент, соответствующие сечению на конце пролетного строения. Значения этих параметров зависят от характера опирания и закрепления концов пролетного строения. При этом в каждом поперечном сечении находят, помимо угла закручивания, также бимомент B_ω, изгибно-крутящий момент M_ω и момент свободного кручения M_t . Этим внутренним усилиям соответствуют нормальные σ и касательные τ напряжения свободного и стесненного σ_ω , τ_t, τ_ω кручения.

σ_ω= 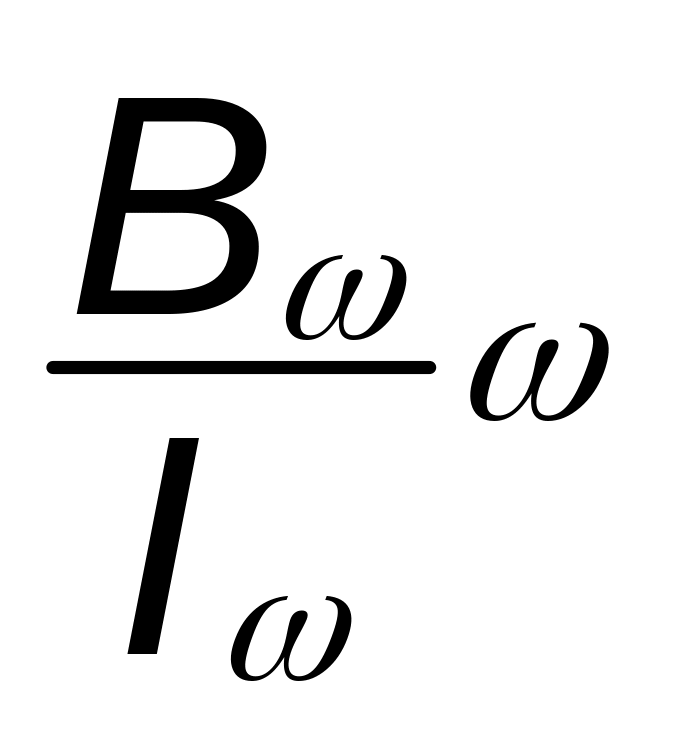τ_t,= τ_ω=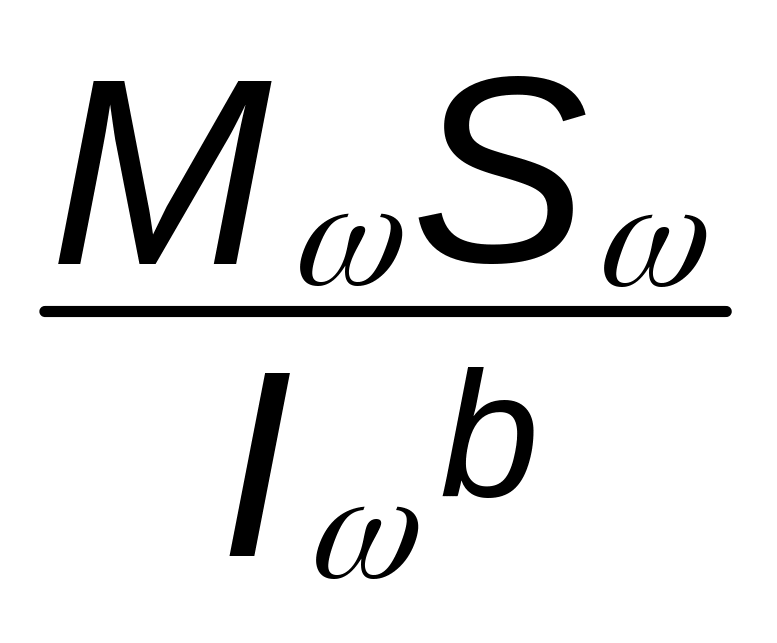

При этом должны быть вычислены дополнительные геометрические характеристики сечения: I_ - главный секториальный момент инерции сечения; S_- главный секториальный статический момент инерции сечения.

Определение нормальных и касательных напряжений от изгиба производится на основе технической теории изгиба.