- •Тема 1. Конструкция разрезных пролетные строений с арматурой, напрягаемой на упоры.
- •1.1.Область применения и компоновка сборных плитных пролетных строений с арматурой, напрягаемой на упоры.
- •1.2. Конструкция и армирование блоков плитных пролетных строений с арматурой, напрягаемой на упоры.
- •1.3. Область применения и компоновка сборных ребристых пролетных строений с арматурой, напрягаемой на упоры.
- •1.4. Конструкция и армирование балок ребристых пролетных строений
- •1.5. Конструкция каркасно-стержневого анкера(рис.1.11)
- •1.6. Сборные разрезные ребристые пролетные строения с арматурой, напрягаемой на бетон
- •1.7. Конструкция продольного шва омоноличивания по плите и конструкция омоноличивания по диафрагмам в ребристых пролетных строениях с напрягаемой арматурой
- •1.8 Тангенциальные опорные части ребристых пролетных строений.
- •Тема 2: « Температурно -неразрезные пролетные строения»
- •1. Понятие о температурно-неразрезных пролетных строениях
- •2.Способы получения температурно-неразрезных пролетных строений.
- •3.Конструкция узла объединения ребристых пролетных строений в температурно -неразрезные.
- •4.Конструкция узла объединения плитных пролетных строений в температурно-неразрезные
- •Тема 3. Неразрезные пролетные строения
- •1. Достоинства неразрезных пролетных строений.
- •2.Виды сборных и монолитных неразрезных пролетных строений
- •3. Конструктивные формы поперечных сечений неразрезных пролетных строений.
- •4. Армирование неразрезных пролетных строений.
- •1) Опорные части стаканного типа(рис.4.1)
- •2) Комбинированные опорные части(рис.4.2)
- •Тема 5: Деформационные швы и сопряжение моста с насыпью
- •Назначение и виды деформационных швов
- •Конструкция закрытого деформационного шва (рис.5.1).
- •Конструкция заполненных деформационных швов(рис. 5.2 и 5.3).
- •Сопряжение моста с насыпью
- •Тема 6 Опоры неразрезных железобетонных пролетных строений автодорожных мостов
- •1. Область применения и конструкция монолитных и сборно-монолитных промежуточных опор. Защита их от ледохода.
- •2.Область применения и конструкция промежуточных опор на оболочках и буровых столбах. Защита их от ледохода.
- •Основная идея и средство приближенного определения усилий в балках с учетом пространственной работы пролетного строения.
- •2.Виды поперечных линий влияния нагрузки и их зависимость от жесткости поперечных связей и вида пролетного строения.
- •3. Расчетные случаи воздействия временной нагрузки ак
- •4.Учет многополосности движения на проезжей части при загружении поперечной линии влияния нагрузки .
- •5.Расчетные формулы для вычисления коэффициента поперечной установки ( рис.7.8)-1 схема загружения)
- •Получение продольных линий влияния изгибающих моментов и поперечных сил для расчетных сечений неразрезных балок и правила их загружения.
- •Расчетные формулы для изгибающих моментов и поперечных сил в сечениях балок неразрезных пролетных строений с учетом их пространственной работы под воздействием постоянной и временной нагрузок.
- •Тема 11: Подбор сечений предварительно напряженных балок.
- •Основы методики строгого расчета при подборе сечения балок
- •Расположение арматуры в поперечном направлении.
- •2. Расположение напрягаемой арматуры в продольном направлении в разрезном пролетном строении.
- •3. Расположение напрягаемой арматуры в продольном направлении в неразрезных пролетных строениях.
- •2.Расчет на прочность сжатых железобетонных элементов мостов с расчетным эксцентриситетом r ( п. 3.69).
- •2. Теоретические основы расчета деформаций пролетных строений железобетонных мостов. Определение деформаций пролетных строений железобетонных мостов: прогибов и углов поворота.
- •3.Факторы, определяющие особенности деформирования железобетонных пролетных строений
- •4. Расчетные формулы сНиП для определения прогибов и углов поворота
- •Учтем далее, что расстояние от центра тяжести площади сжатого бетона до центра всего сечения определяется формулой
- •2.Расчет местных напряжений в зоне передачи усилий предварительного напряжения.
- •Диафрагменные ребристые или коробчатые пролетные строения с недеформируемым контуром поперечного сечения, составленного из тонкостенных стержней.
- •Бездиафрагменные коробчатые пролетные строения с замкнутым деформируемым поперечным сечением (рис.19.5).
- •Тема 20 .Рамные железобетонные мосты.
- •1. Схемы и виды рамных железобетонных мостов. Особенности рамных мостов.
- •3. Особенности конструкций рамных мостов малых пролетов.
- •1. Типы поперечных сечений ригелей рамных мостов средних и больших пролетов и особенности
- •3. Узел опирания подвесной балки рамно-балочного моста на ригель(рис.21.4)
- •4. Пример современного рамного моста
- •5. Особенности расчета рамных мостов
- •1. Особенности и области применения арочных железобетонных мостов.
- •2. Виды арочных железобетонных мостов
- •3. Конструкции арочных мостов со сплошными сводами
- •3. Конструкции мостов с раздельными арками.
- •3.4. Форма и размеры поперечного сечения арок
- •3.5. Изменение сечения арки по длине пролета
- •3.6. Армирование раздельных арок.
- •3.7. Шарниры арочных мостов
- •3.8. Особенности конструкции арочных мостов с ездою понизу и посередине.
- •3.9. Опоры арочных мостов
- •Материалы для деревянных мостов.
- •2.Особенности строения древесины .
- •Особенности механических свойств древесины.
- •5. Компоновка и основные типы конструктивных решений деревянных мостов малых пролетов.
- •6. Конструкция проезжей части
- •7. Конструкции пролетных строений из простых прогонов
- •8. Конструкции пролетных строений из сложных прогонов
- •9. Конструкции пролетных строений из клеефанерных блоков
- •10. Опоры мостов малых пролетов
- •11. Сопряжение моста с насыпями подходов
- •1. Компоновка и основные типы конструктивных решений деревянных мостов
- •2. Конструкция проезжей части мостов
- •3. Пролетные строения с клееными балками
- •4. Пролетные строения с дерево - металлическими фермами Гау—Журавского
- •5. Пролетные строения с дощато-гвоздевыми фермами
Учтем далее, что расстояние от центра тяжести площади сжатого бетона до центра всего сечения определяется формулой

Тогда
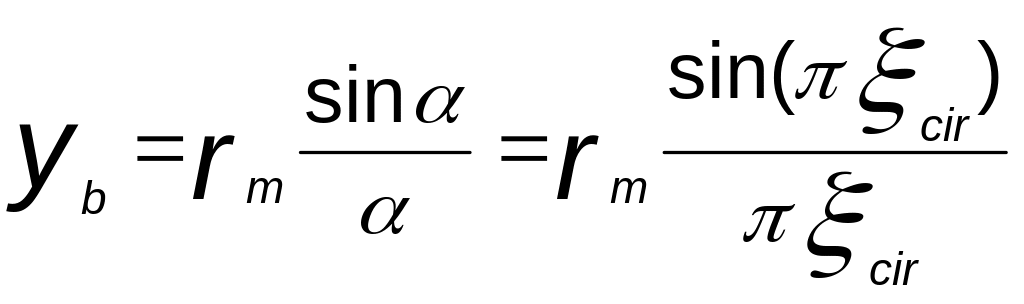 ,
(3)
,
(3)
а
расстояние от равнодействующей усилий
в сжатой арматуре до центра сечения
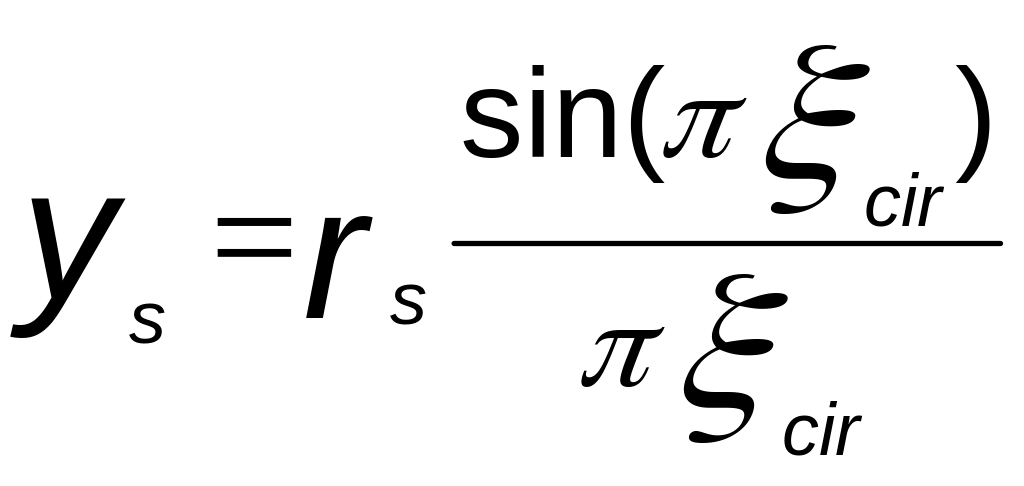 (4)
(4)
Принимая затем площадь арматуры равномерно распределенной по окружности радиуса rs, условие прочности с учетом прогиба элемента можно записать в таком виде:
![]() (5)
(5)
Подставляя
в (5) значения
![]() ,
,
![]() ,
,
![]() получим
получим
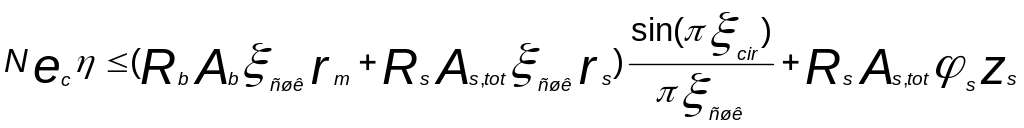
После
сокращения на![]() получаем
получаем

Значения
zs
и
![]() определяются по эмпирическим
формулам:
определяются по эмпирическим
формулам:

Относительную площадь сжатой зоны бетона находят из условия равенства нулю суммы проекций всех сил на горизонтальную ось:
![]()
После
замены
![]() и приведения подобных членов получаем
и приведения подобных членов получаем
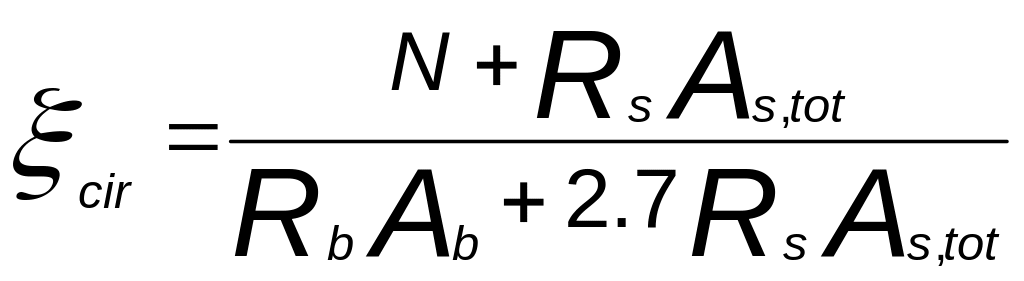
Если
при этом будет получено![]() ,т.е.
при относительно малой площади сжатого
бетона, то прочность сечения проверяют
по условию
,т.е.
при относительно малой площади сжатого
бетона, то прочность сечения проверяют
по условию
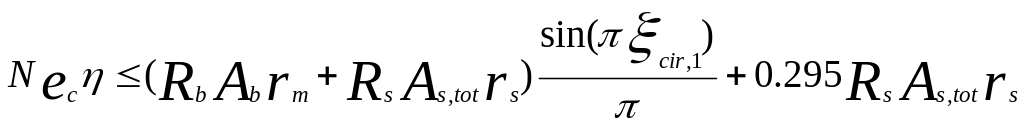
где
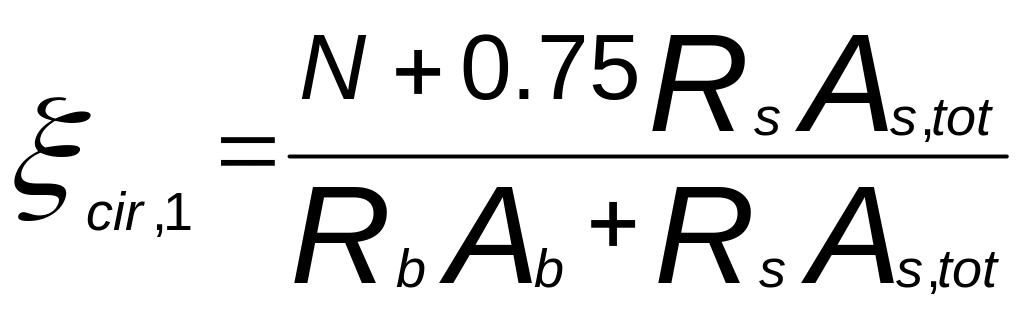 а
при значительной площади сжатого бетона
( при
а
при значительной площади сжатого бетона
( при
![]() )
влиянием растянутой арматуры
пренебрегают(
)
влиянием растянутой арматуры
пренебрегают(![]() )
и прочность сечения проверяют по условию
)
и прочность сечения проверяют по условию
 ,
в котором
,
в котором
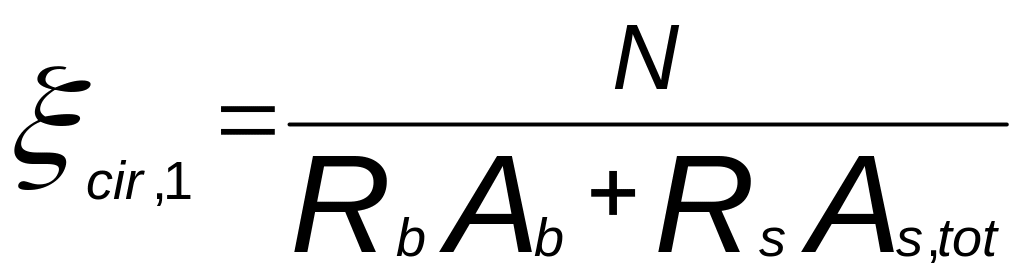
При малых эксцентриситетах ( с учетом случайного) продольной силы, когда она не выходит за пределы ядра сечения, то сечение следует проверять на устойчивость по формуле
![]()
Тема лекции18: Основы расчета местных напряжений.
Расчет на местное сжатие железобетонных элементов мостов
(выполняется в соответствии с п. 3.89 и 3.90 СНиП2.05.03-84*).
В местах расположения опорных частей бетон пролетных строений и опор необходимо рассчитывать на местное сжатие ( смятие )(рис.18.1)
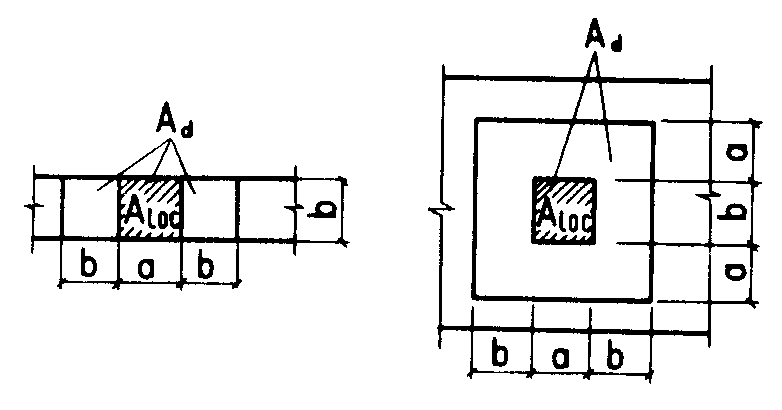
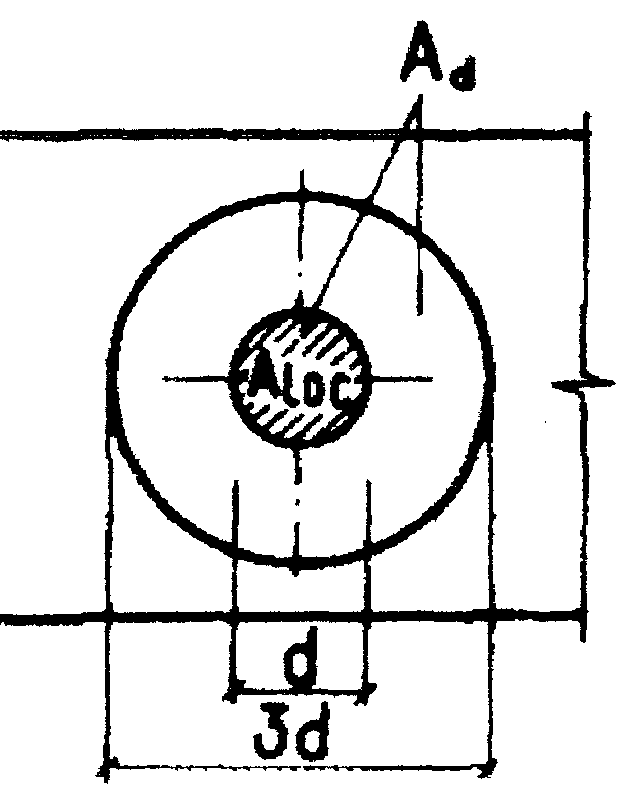
Рис.18.1. Схемы расположения расчетных площадей Ad в зависимости от положения площадей смятия Aloc
При расчете на смятие элементов из бетона, не имеющего косвенного армирования должно выполняться условие
![]()
где![]() -
продольная сжимающая сила;
-
продольная сжимающая сила;
![]() -
коэффициент, принимаемый равным 1 при
равномерном распределении местной
нагрузки на площади смятия ;-0.75 при
неравномерном распределении;
-
коэффициент, принимаемый равным 1 при
равномерном распределении местной
нагрузки на площади смятия ;-0.75 при
неравномерном распределении;
![]() -
площадь смятия;
-
площадь смятия;
![]() -
расчетное сопротивление бетона смятию,
определяемое по формулам
-
расчетное сопротивление бетона смятию,
определяемое по формулам
![]()
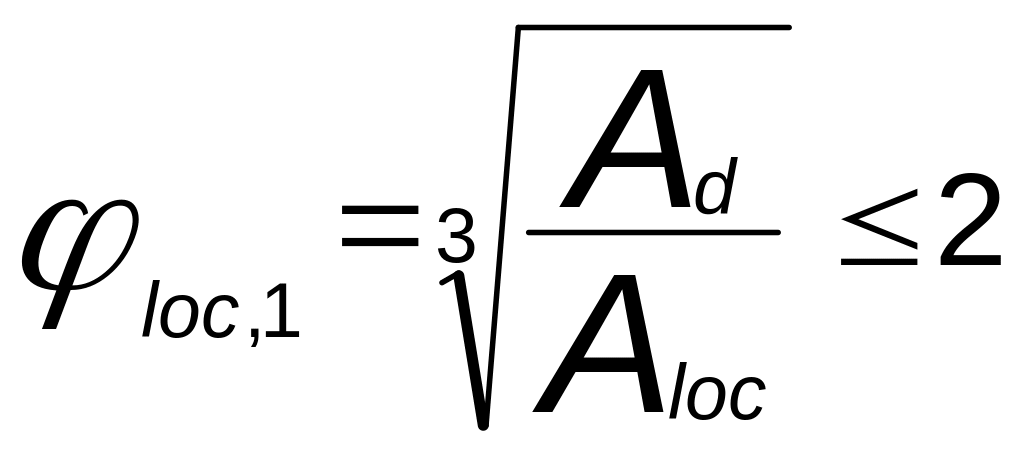
![]() -
расчетное сопротивление бетона
растяжению;
-
расчетное сопротивление бетона
растяжению;
![]() -
расчетная площадь, симметричная по
отношению к площади смятия, принимаемая
по схемам ниже приведенного рисунка.
-
расчетная площадь, симметричная по
отношению к площади смятия, принимаемая
по схемам ниже приведенного рисунка.
При расчете на смятие элементов с косвенным армированием в виде сварных поперечных сеток должно удовлетворяться условие
![]()
где
- площадь смятия;
![]() -
приведенная прочность бетона сжатию,
определяемая по формуле
-
приведенная прочность бетона сжатию,
определяемая по формуле
![]()
где
![]() -
в МПа
-
в МПа
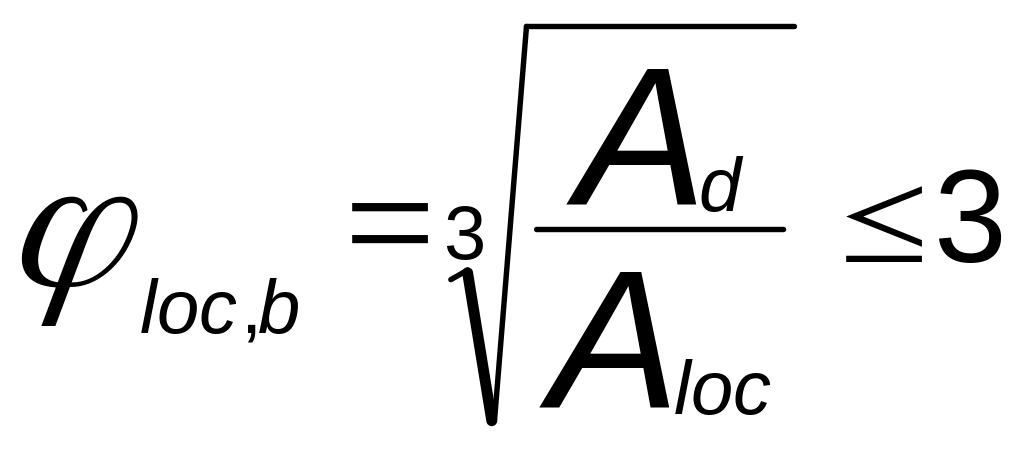
![]() -
соответственно
коэффициент эффективности косвенного
армирования и коэффициент армирования
сечения сетками или спиралями , вычисляемые
по формулам 83,84 и 87 СНиП 2.05.03-84*.
-
соответственно
коэффициент эффективности косвенного
армирования и коэффициент армирования
сечения сетками или спиралями , вычисляемые
по формулам 83,84 и 87 СНиП 2.05.03-84*.

![]() -площадь
бетона, заключенного внутри контура
сеток косвенного армирования, считая
по их крайним стержням, при этом должно
удовлетворяться условие
-площадь
бетона, заключенного внутри контура
сеток косвенного армирования, считая
по их крайним стержням, при этом должно
удовлетворяться условие
![]()
2.Расчет местных напряжений в зоне передачи усилий предварительного напряжения.
В предварительно напряженных железобетонных конструкциях в зонах передачи на бетон усилий предварительного натяжения от анкеров возникает сложное напряженное состояние. местные напряжения.
На рис.18.1,а схематично показаны траектории главных напряжений при расположении анкеров на торце (натяжение арматуры на бетон) а на рис.18.1,б – в теле балки ( натяжение арматуры на упоры).
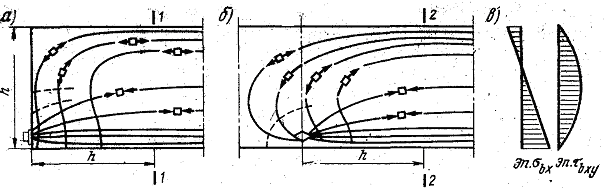
Рис.18.1.Линии главных напряжений в теле балки: а- при расположении анкера на торце балки; б- при расположении анкера в теле балки: в- эпюра нормальных и касательных напряжений по сечениям 1-1 и 2-2.
Главные растягивающие напряжения могут быть больше сопротивления бетона растяжению, что приводит к образованию и раскрытию трещин, если не принять необходимых конструктивных мер.
Трещины раскрываются перпендикулярно траекториям главных растягивающих напряжений, возможное их положение показано на рис.18.1. штриховой линией.
Местные напряжения проявляются на сравнительно небольшом участке от места приложения усилия. Установлено, что на расстоянии от анкеров, превышающем высоту сечения h нормальные и касательные напряжения распределяются по вертикальному сечению по законам сопротивления упругих материалов(рис.18.1,в).
На участках вблизи анкеров напряжения могут быть определены численными методами с использованием положений теории упругости. Эти расчеты сложны и не обеспечивают высокой точности, так как исходят из условий упругой работы бетона. В связи с этим при расчете мостовых конструкций получил приближенный способ, в основу которого положены условия равновесия участков элементов, выделяемых вблизи анкеров вертикальными и горизонтальными сечениями.
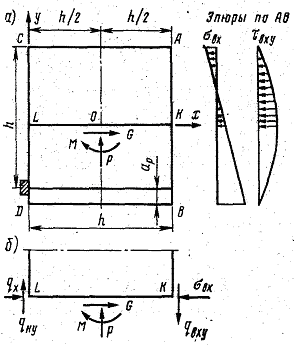
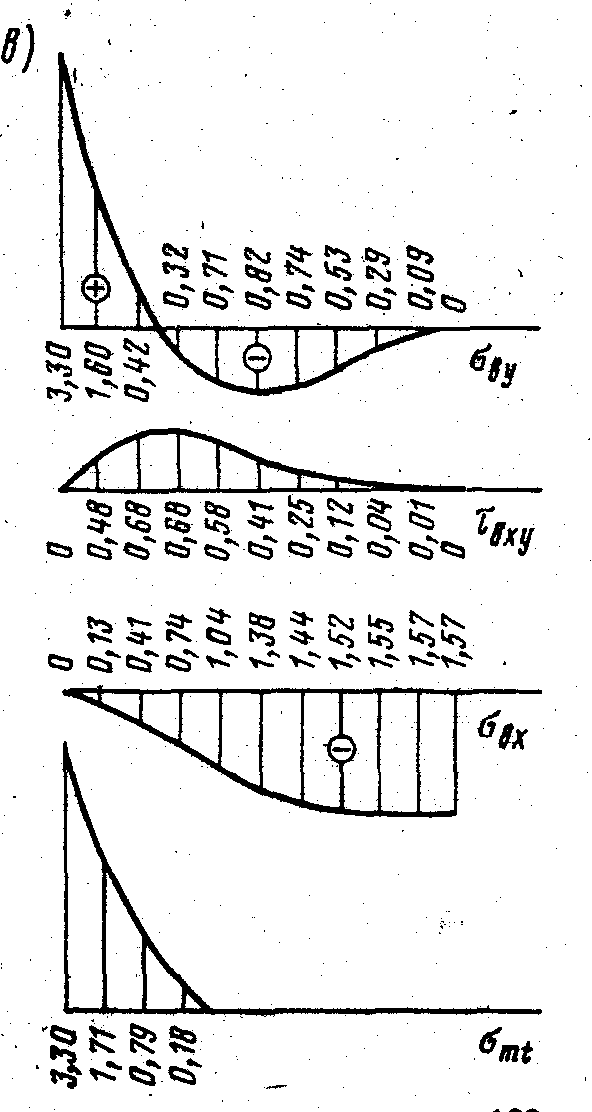
Рис.18.2.Идеология определения напряжений по продольным сечениям концевого блока
Местные напряжения на участке балки между её торцом и сечением АВ(Рис.18.2), удаленном от торца балки на расстояние h, в соответствии с этим способом определяются в следующем порядке:
- в сечении АВ по формулам сопротивления материалов определяют эпюры нормальных и касательных напряжений от изгибающего момента и поперечной силы, действующих в этом сечении;
- горизонтальным сечением LK выделяют блок LCKA и из условия его равновесия определяют внутренние усилия P, M и G, приложенные к середине сечения LK, на расстоянии 0.5 h от торца балки.
- находят напряжения σby, τbxy, σbx по сечению LK по формулам (при прямоугольной форме сечения LK):
σby=k1M/(bh2) +k2P/(bh);
τbxy=k3G/(bh) +k4qxy +k5 τbxy(k)
σbx=k6qx+k7 σbx(k)
где qx и qxy - нормальные и касательные напряжения в точке L горизонтального сечения LK в случае, когда сечение пересекает анкер; в противном случае они равны нулю;
σbx(k) и τbxy(k) -нормальные и касательные напряжения в точке К горизонтального сечения LK, определяемые по эпюрам напряжений в сечении А-В.
Значение коэффициентов К1 – К7 для разных схем приложения усилий бетона приведены в монографии Гибшман Е.Е., Гибшман М.Е. «Теория и расчет предварительно напряженных железобетонных мостов» 1963г Они зависят от положения точки на сечении, для которой вычисляются напряжения.
По данным вычисления могут быть построены эпюры нормальных и касательных напряжений и вычислены главные растягивающие напряжения.
Приемы определения местных напряжений для более сложных случаев имеются в специальной литературе.( Е.Е. Гибшман, М.Е. Гибшман. Теория и расчет предварительно напряженных железобетонных мостов.1963г)
В результате действия местных напряжений в бетоне могут появиться трещины Для их предотвращения можно рекомендовать установку специальной арматуры: напрягаемой или ненапрягаемой(рис.18.3).
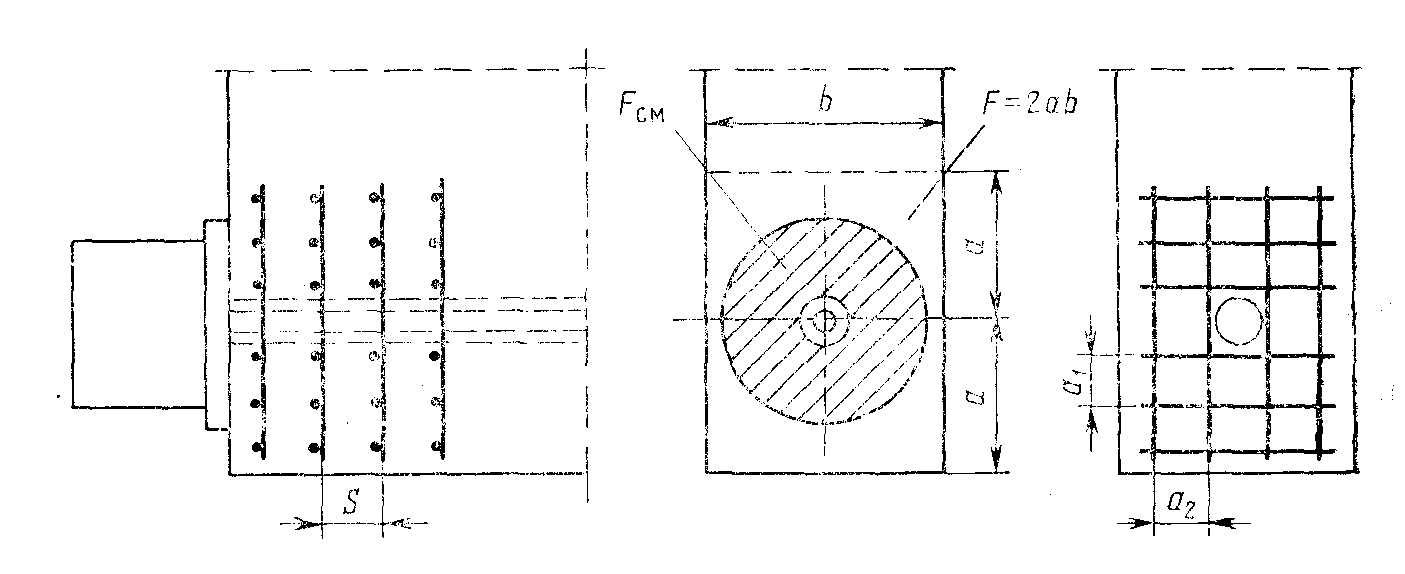
Рис.18.3. Армирование бетона в зоне размещения анкера.
Лекции 19. Тема лекции: «Виды расчетных моделей пролетных строений железобетонных мостов, особенности их работы и расчета.
Литература по теме лекции § 6.2 [7] (Проектирование транспортных сооружений, М.Е. Гибшман, В.И. Попов В.И. 1988)
Пролетные строения железобетонных мостовых сооружений по конструктивным особенностям поперечных сечений и связанным с ними характером напряженного и деформированного состояния можно разделить на следующие 5 групп:
Пролетные строения (рис.1) со сплошным (или с небольшими пустотами) поперечным сечением, отношение ширины В которого к высоте Н не превышает 7 - 8, а размеры поперечного сечения значительно меньше длины пролета.
В

Н <<L
Рис.19.1
С расчетной точки зрения такие пролетные строения можно рассматривать как массивные упругие брусья. Под воздействием внешних нагрузок они изгибаются и закручиваются без изменения контура поперечного сечения.
Расчет этих пролетных строений и их систем производится обычно на основе классической теории стержневых систем:
на изгиб в одной плоскости с использованием дифференциального уравнения(1),
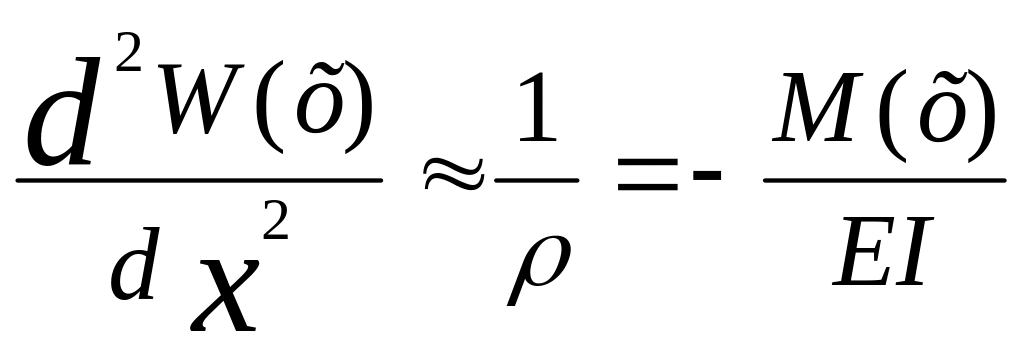 (1)
(1)
где W- упругий прогиб в плоскости изменения кривизны; М- изгибающий момент, EI- жесткость бруса при изгибе;
а кручение с использованием уравнением (2).
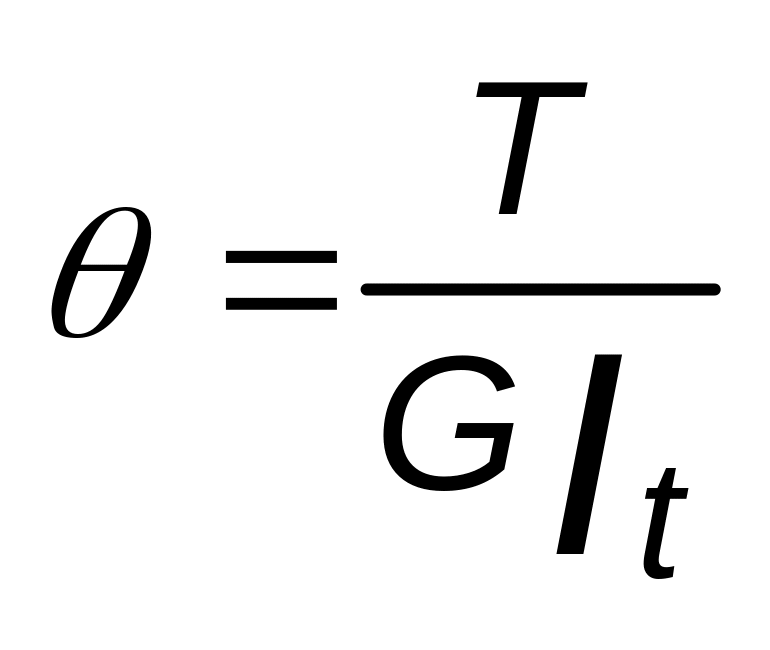 (2)
(2)
где
θ- угол закручивания, Т- крутящий
момент,![]() –
жесткость бруса при кручении.
–
жесткость бруса при кручении.
Уравнения (1) и (2) позволяют определить внутренние силовые факторы от изгиба и кручения, по которым находятся соответствующие напряжения.
Пролетные строения (рис.19.2) со сплошным (или с небольшими пустотами) поперечным сечением, отношение ширины которого к высоте больше 7-8, а размеры ширины сечения значительно меньше длины пролета.
B

H
. B/H > 7-8 B << L
Рис.19.2. Поперечное сечение пролетного строения в виде упругой плиты.
Под воздействием внешних нагрузок такие пролетные строения изгибаются и закручиваются с искривлением контура поперечного сечения. Для этой группы пролетных строений возможна расчетная модель в виде упругих плит.
Расчет этих пролетных строений можно выполнять методами теории упругости как изотропной пластинки, если считать, что изгибная жесткость плиты в продольном и поперечном направлениях одинакова.
При заданной функции нагрузки q(x,y) решение задачи расчета плиты в этом случае заключается в получении функции прогибов w(x,y), удовлетворяющей граничным условиям и дифференциальному уравнению (3) изгиба изотропной пластинки
![]() (3)
(3)
где x, y --- координатные оси; q- внешняя распределенная нагрузка; D – цилиндрическая жесткость, являющаяся постоянной величиной и определяемая по формуле
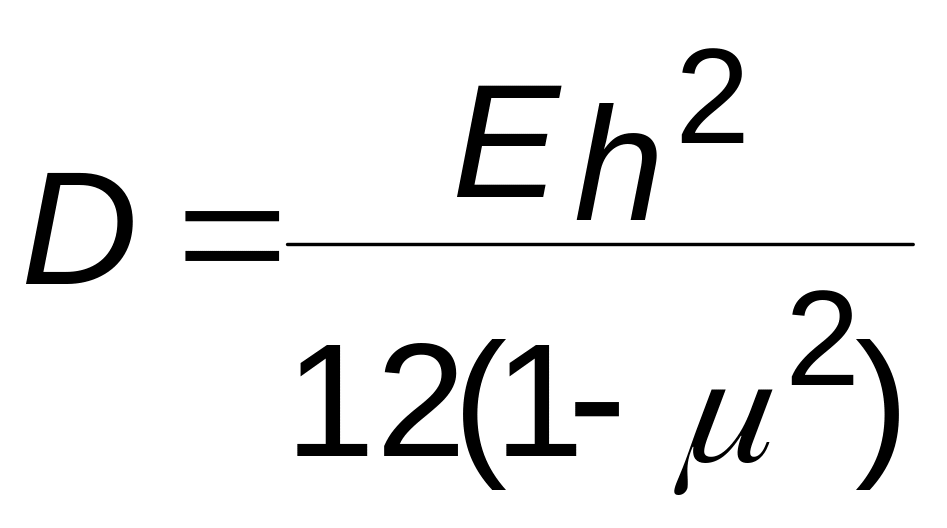
где E, μ- модуль упругости и коэффициент Пуассона материала пролетного строения; h- толщина плитного пролетного строения.
Дифференциальное уравнение (3) решается с учетом граничных условий по кромкам плиты. Для однопролетной плиты (рис.3а) по опорным кромкам прогибы W, изгибающие моменты Mx и углы поворота dW/dy в направлении оси х равны нулю, а по боковым граням Qy= My= Mxy= 0
В многопролетных строениях к граничным условиям необходимо добавлять условия совместности деформаций в надопорных сечениях (рис.19.3б) ( изгибающие моменты и поперечные силы равны по величине и противоположны по знаку).
Определение функции w(x,y), удовлетворяющей уравнению (3) и граничным условиям, представляет собой сложную математическую задачу. (Обычно используется метод Фурье).
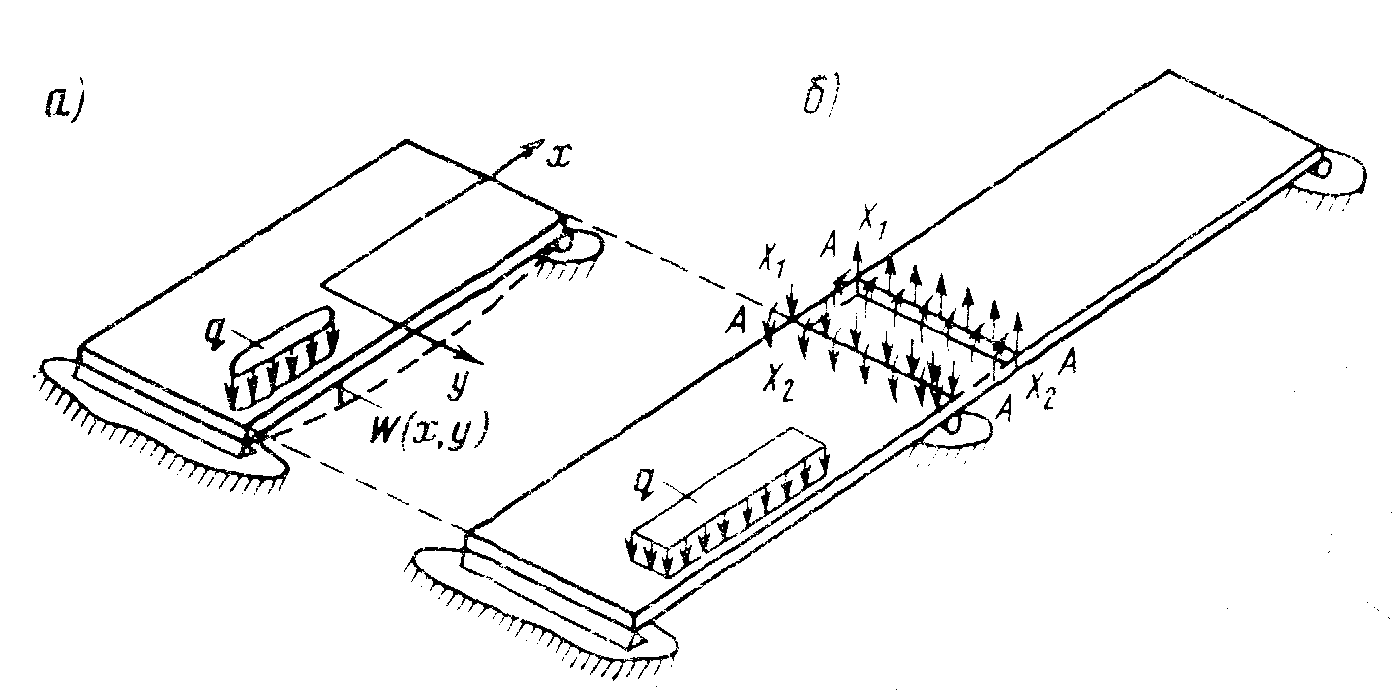 Рис.19.3.Схемы
к расчету плитных пролетных строений
как упругих пластинок.
Рис.19.3.Схемы
к расчету плитных пролетных строений
как упругих пластинок.
При найденной функции w(x,y) необходимые расчетные силовые факторы в любой точке плиты определяются известными соотношениями теории упругости
![]()
![]()
![]()
![]()
![]()
где –Mx ,My,Mxy – изгибающие моменты на единицу длины сечения:
Qx, Qy – поперечные силы на единицу длины сечения.
Плитное пролетное строение обычно имеет различную изгибную жесткость в продольном и поперечном направлениях. Плиту с учетом этого следует рассматривать как ортотропную и использовать при этом дифференциальное уравнение изгиба ортотропной пластинки следующего вида
![]() (4)
(4)
где
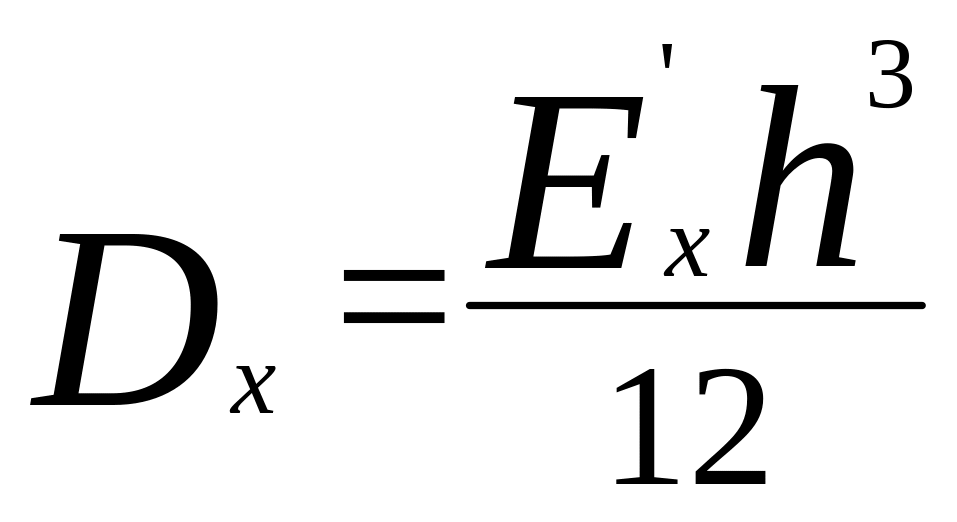 :
: ;
; ;
;