2. Теоретические основы расчета деформаций пролетных строений железобетонных мостов. Определение деформаций пролетных строений железобетонных мостов: прогибов и углов поворота.

В качестве теоретической основы расчета деформаций пролетных строений железобетонных и других мостов используется интеграл Мора.

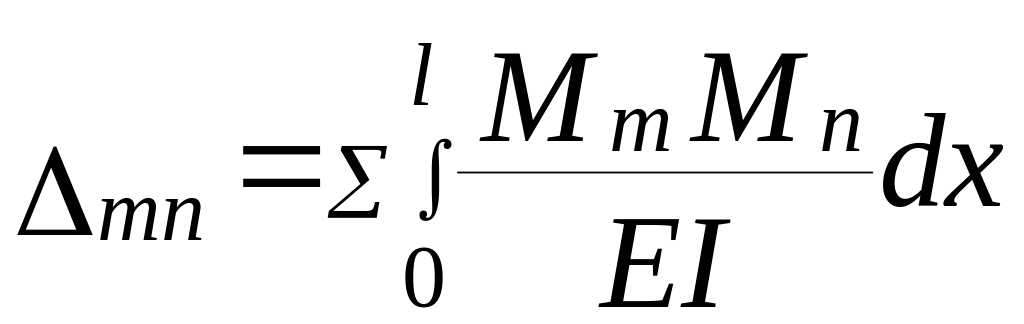, (1)

где - перемещение по направлению фиктивной единичной силы P=1, вызванное действием реальной произвольной группы сил n.

- Mm(X) - изгибающий момент от фиктивной единичной нагрузки в функции координаты Х произвольного сечения,

- Mn(Х) - изгибающий момент от заданной нагрузки в функции координаты Х произвольного сечения

При решении задачи рассматривается два состояния пролетного строения:

а. В первом его (действительном) состоянии на него действует реальная система сил.

б.Во втором (единичном или фиктивном) состоянии к пролетному строению приложена лишь одна сосредоточенная фиктивная сила.

При вычислении прогиба в какой- то точке по длине пролета, в качестве единичной силы служит безразмерная фиктивная сосредоточенная сила, приложенная в этой точке. При вычислении угла поворота в какой то точке пролетного строения в качестве единичной силы выступает сосредоточенный безразмерный фиктивный момент, приложенный в той же точке.

в.Находятся выражения Mn (X) и Mm (X), подставляются в правую часть формулы (1) и при интегрировании по участкам в пределах всего пролетного строения определяется искомое перемещение . Если положительно, то перемещение совпадает с направлением единичной силы, а если отрицательно, то противоположно этому направлению.

3.Факторы, определяющие особенности деформирования железобетонных пролетных строений

а. Пролетное строение в общем случае находится под воздействием трех видов нагрузок:

- постоянной нагрузки от собственного веса,

- временной подвижной нагрузки,

-усилий в напрягаемой арматуре.

б. Жесткость сечений пролетного строения может изменяться по длине пролетного строения.

в. Жесткость сечений пролетного строения, в связи с проявлением ползучести бетона, зависит и от продолжительности воздействия нагрузки.

Интеграл Мора позволяет учитывать эти особенности, поскольку жесткость под интегралом может быть представлена в функции координаты Х, кроме того, знак суммы позволяет интегрировать воздействие различных сил при различной жесткости отдельно.

4. Расчетные формулы сНиП для определения прогибов и углов поворота

Прогиб f или угол поворота , вызванный изгибом пролетного строения рекомендуется определять по формуле

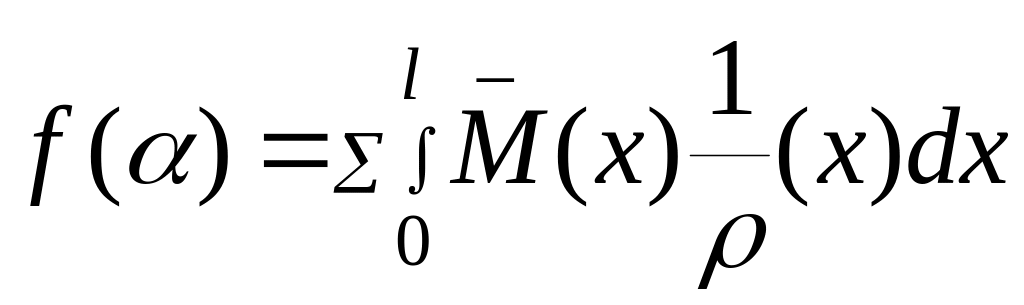(2)

где - при определении прогиба f- функция изгибающего момента от единичной силы, приложенной по направлению искомого прогиба f, при определении угла поворота -функция изгибающего момента, приложенного по направлению искомого угла поворота.

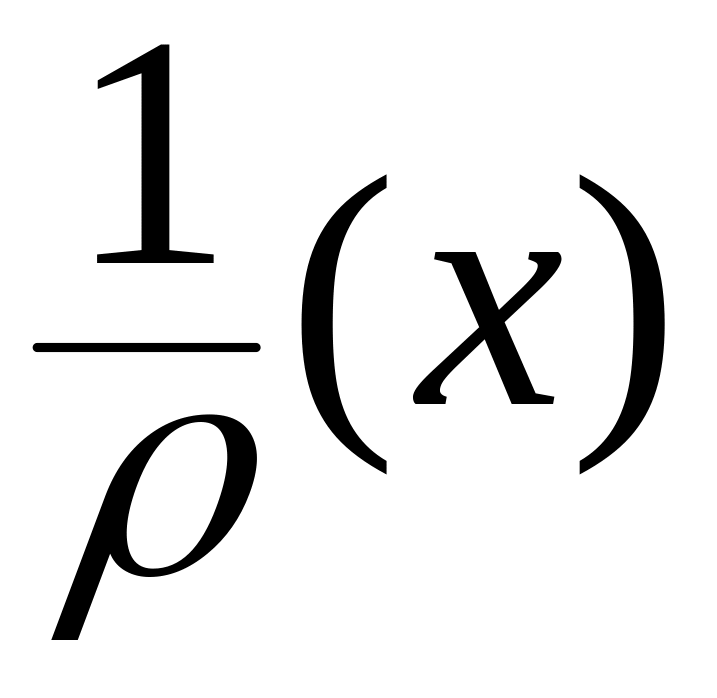- кривизна пролетного строения в том же сечении от заданной действительной нагрузки.

В формуле (2) суммирование производится по всем участкам по длине пролета, различающимся законами изменения величин и .

Вычисление допускается производить численными приемами, используя выражение

,

в котором и -средние величины момента и кривизны на отдельных участках длиной , где изменение указанных параметров имеет плавный характер.

Кривизну предварительно напряженных элементов, в которых пояса отнесены к категориям требований по трещиностойкости 2а, 2б и 3б допускается определять как для сплошного сечения по формуле

где- Mp, Mg. M- моменты в рассматриваемом сечении, создаваемые соответственно усилием в напрягаемой арматуре, постоянной и временной нагрузками,

- жесткости сечения при длительном воздействии соответственно усилия в напрягаемой арматуре и постоянной нагрузки ,

B- жесткость сплошного сечения при кратковременном действии нагрузок.

Значения жесткости и B определяется по обязательному приложению 13 СНиП 2.05.03-84

Общий вид этих формул можно представить следующим образом

,

где к- коэффициент, учитывающий влияние неупругих деформаций бетона при кратковременном приложении нагрузки и принимаемый равным 0.85.

=C_lim,iE_bi- приведенная величина предельной характеристики ползучести бетона, определяемая по п.2-3. приложения13 к СНиП 2.05.03-84*

Лекция 17 Тема.Расчет внецентренно - сжатых железобетонных элементов мостов кольцевого сечения.

Для расчета на прочность элементов кольцевого сечения используются формулы, обеспечивающие достаточную для практических расчетов точность при соотношении внутреннего и наружного диаметров и ненапрягаемой арматуре, состоящей не менее чем из шести стержней, равномерно распределенных по окружности. Они приведены в СНиП 2.05.03-84 . Ниже дается вывод этих формул и принятые при этом допущения

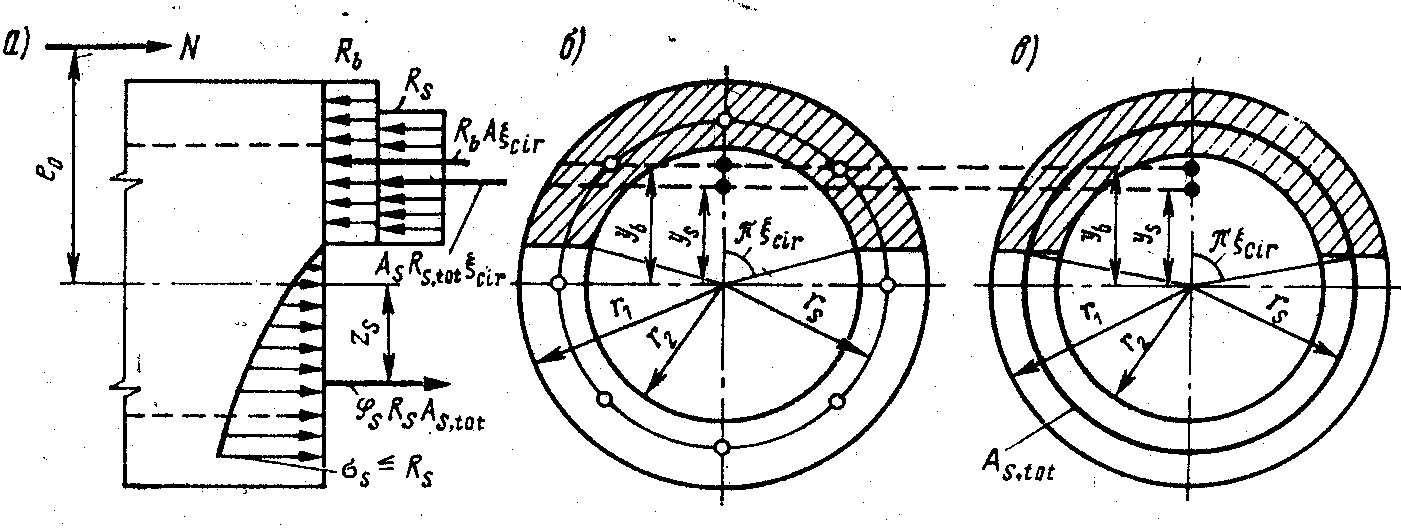
Рис17.1. Схема для расчета внецентренно сжатого кольцевого сечения

При выводе формул считается, что:

1. Арматура равномерно распределена по окружности радиуса r_s, равного расстоянию oт центра сечения до арматурных стержней.

2. Напряжения в бетоне и арматуре сжатой зоны равны их расчетным сопротивлениям R_b и R_s

3. Напряжения в арматуре растянутой зоны зависят от положения стержней, средние напряжения в ней равны .

4. Равнодействующая усилий в растянутой арматуре проходит на расстоянии Zs от оси сечения.

Представим относительную площадь сжатой зоны бетона как

(1)

где r_m = (r₁ – r₂) / 2

Из (1) получаем значение угла, ограничивающего сжатую зону,

(2)