1. Теория и основные понятия

Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Графами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых.С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.

1.1 Определения теории графов

Простым графом G называется пара (V, E), где V - непустое конечное множество, элементы которого называются вершинами графа, а E - конечное множество неупорядоченных пар различных элементов из V, элементы множества E называются ребрами.

В дальнейшем будем рассматривать только простые графы, опуская при этом слово простые.

Если (u,v) - некоторое ребро графа G, то вершины u и v называются смежными, а вершины u и ребро (u,v), также как вершина v и ребро (u,v), называются инцидентными друг другу. Степенью вершины v в графе G называется число ребер графа G, инцидентных вершине v.

	v3	v4
v1			v5
v2			v6

Рисунок 0 - Пример графа

В данном примере V = {v₁, v₂, v₃, v₄, v₅, v₆}, E = {(v₁, v₂), (v₂, v₃), (v₁, v₃), (v₃, v₄), (v₄, v₅), (v₄, v₆), (v₅, v₆)}

Пусть G = (V, E) - некоторый граф, u и v - его вершины. Маршрутом в графе G, соединяющим вершины  u и v, называется конечная чередующаяся последовательность вершин и ребер вида v₁, e₁, v₂, e₂,...,e_k-1, v_k, где v₁,...,v_k из V, а e₁,...,e_k-1 из E. Маршрут называют цепью, если все его ребра различны. Цепь называют путем (или простой цепью), если все ее вершины кроме, быть может, концевых различны. Если начальная и конечная вершина пути совпадают, то его называют замкнутым путем или циклом.

Граф называется связным графом, если для любых двух его вершин существует соединяющий их маршрут.

Теперь мы можем определить особый класс графов - деревья. Деревом называется связный граф без циклов.

Ориентированным графом D называется пара (V, A), где V - непустое конечное множество, элементы которого называются вершинами графа, а A - конечное множество упорядоченных пар различных элементов из V, элементы множества A называются дугами.

Подобно графам для ориентированных графов вводятся понятие смежности вершин, понятие инцидентности и так далее.

Основанием ориентированного графа D = (V, A), называется граф G = (V, E), где E = A, то есть упорядоченные пары вершин заменяются на неупорядоченнные.

Транспортной сетью называется конечный Связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c( ), называемое пропускной способностью дуги, и существует:

1)   ровно одна вершина , в которую не заходит ни одна дуга, называемая источником или началом сети;

2)   ровно одна вершина , из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.

Потоком сети называется неотрицательная функция f(1) такая, что f(e) меньше или равно c(e). (Поток не может превышать пропускную способность дуги.)

Дуга называется насыщенной потоком f, если (Поток называется полным, если содержит насыщенную дугу f(e)=c(e).)

     Разрезом L  сети G(V,E) называется множество насыщенных дуг, отделяющих источник s от стока t.

1.2 Поток в транспортной сети.

Функция , определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если:

     для любой дуги  величина , называемая потоком по дуге , удовлетворяет условию ;

     для любой промежуточной вершины v выполняется равенство

т.е. сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.

Для любого допустимого потока  в транспортной сети D выполняется равенство:

  По определению допустимого потока  имеем:

       

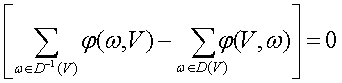
  Заметим, что для каждой дуги  где , величина  входит в левую часть равенства лишь один раз и при этом со знаком плюс. Аналогично для каждой дуги , величина входит в левую часть равенства (2) лишь один раз и при этом со знаком минус. С другой стороны, для каждой дуги  величина  входит в левую часть равенства (2) один раз со знаком плюс (при ) и один раз со знаком минус (при ), что в сумме даёт нулевой вклад в левую часть равенства (2). Учитывая сказанное, заключаем, что из равенства (2) следует справедливость равенства (1).

  Величиной потока  в транспортной сети D называется величина , равная сумме потоков по всем дугам, заходящим в , или, что то же самое – величина, равная сумме потоков по всем дугам, исходящим из

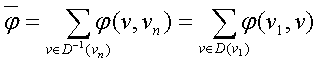
  Пусть  - допустимый поток в транспортной сети D. Дуга  называется насыщенной, если поток по ней равен её пропускной способности, т.е. если . Поток  называется полным, если любой путь в D из  содержит, по крайней мере, одну насыщенную дугу. Поток  называется максимальным, если его величина  принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D.

  Очевидно, что максимальный поток  обязательно является полным (т.к. в противном случае в D существует некоторая простая цепь  из V1 в Vn, не содержащая насыщенных дуг, а следовательно, можно увеличить на единицу потоки по всем дугам из  и тем самым увеличить на единицу , что противоречит условию максимальности потока). Обратная же, вообще говоря, неверно. Существуют полные потоки, не являющиеся максимальными. Тем на менее полный поток можно рассматривать как некоторое приближение к максимальному потоку.

Теорема Форда-Фалкерсона

Пусть D – транспортная сеть,  - допустимый поток в этой сети,  - множество вершин  таких, что длина минимального пути из  в  в орграфе приращений  равна нулю. Тогда, если , то  - максимальный поток, величина которого равна .

Пусть . Тогда выполняется равенство

         (1)

Если , так как в противном случае, используя  имеем , а следовательно, в силу  существует путь нулевой длины из  в , что противоречит условию . Но тогда из (1) получаем

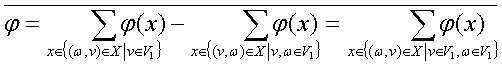(2)

Следствие 1. Используя теорему Форда-Фалкерсона получаем, что величина максимального потока в транспортной сети равна пропускной способности минимального разреза.

Следствие 2. Пусть  - допустимый поток в транспортной сети D. Тогда, если длина минимального пути из v1 в vn в орграфе приращений  равна бесконечности, то  - максимальный поток.

0. 1.3 Формализованное задание графа

Граф задается на множестве вершин V и множестве ребер Е. Наиболее простое описание графа – графическое (рис. 1) и составление таблицы соответствия ребер и вершин.

Для удобства описания графа часто используют матрицы инциденций, смежности, циклов, разрезов и путей.

Рисунок 1 – Исходный граф G для варианта №4

Описание графа с помощью таблицы приведено в таблице 1.1

Таблица 1.1

E	8	3	3	6	2	4	3	5	6
V	v1, v2	v2, v4	v4, v6	v5, v6	v5, v4	v1, v3	v3,v2	v3,v5	v2,v5

Описание графа с помощью фактор – множества выражается следующим образом:

(1.1)

Описание графа с помощью матрицы инциденций

Для графа G, имеющего n вершин и m ребер матрица инциденций имеет размерность n x m. Строки этой матрицы соответствуют вершинам, а столбцы – ребрам графа. Элемент а_ij=1, если j-ое ребро инцидентно i-ой вершине и а_ij=0 в противном случае.

Для графа, представленного на рисунке 1 матрица инциденций имеет вид:

Таблица 1.2

	E1	E2	E3	E4	E5	E6	E7	E8	E9
V1	1	1	0	0	0	0	0	0	0
V2	-1	0	1	1	-1	0	0	0	0
V3	0	-1	0	0	1	1	0	0	0
V4	0	0	-1	0	0	0	1	1	0
V5	0	0	0	-1	0	-1	-1	0	1
V6	0	0	0	0	0	0	0	-1	-1

Описание графа с помощью матрицы смежности вершин

Для графа G, имеющего n вершин матрица смежности вершин имеет размерность n x n. Элемент v_ij этой матрицы равен числу ребер, инцидентных одновременно i-ой и j-ой вершинам графа.

Для графа, представленного на рисунке 1 матрица смежности вершин имеет вид:

Таблица 1.3

	V1	V2	V3	V4	V5	V6
V1	0	1	1	0	0	0
V2	0	0	0	1	1	0
V3	0	1	0	0	1	0
V4	0	0	0	0	1	1
V5	0	0	0	0	0	1
V6	0	0	0	0	0	0

Описание графа с помощью матрицы циклов

Для графа G, имеющего n вершин и m ребер, матрица циклов имеет размерность к x m, где к – число циклов в графе. Элемент этой матрицы с_ij=1, если j-ое ребро входит в i-ый цикл и с_ij=0 в противном случае.

Поскольку циклов в данном ориентированном графе нет, представлять в виде матрицы циклов не имеет смысла.

Описание графа с помощью матрицы разрезов

Если задан связный граф G=(V, E) и множество его вершин разбито на два непустых подмножества W и W^/, то множество ребер, соединяющих W с W^/ называют разрезом. Простым называют разрез, разбивающий связный граф только на две компоненты связности. С использованием простых разрезов можно построить матрицу разрезов графа.

Для графа G, имеющего n вершин и m ребер, матрица разрезов имеет размерность l x m, где l – число разрезов на графе. Элемент этой матрицы к_ij=1, если j-ое ребро входит в i-ый разрез и к_ij=0 в противном случае.

Для графа, представленного на рисунке 1 матрица разрезов имеет вид:

Таблица 1.4

	E1	E2	E3	E4	E5	E6	E7	E8	E9
K1	1	1
K2								1	1
K3						1	1	-1
K4	1				-1	1
K5		1	1		1
K6			-1				-1		-1
K7		1			-1		-1		1
K8	1				1		-1	1
K9			-1			-1

Описание графа с помощью матрицы путей

Для ориентированных графов матрица путей составляется, если есть хотя бы один путь, ведущий из начальной в конечную вершину. Элемент матрицы p_ij =1, если j-ая дуга принадлежит i-ому пути и p_ij = 0 в противном случае.

Для графа, представленного на рисунке 1 матрица путей имеет вид:

Таблица 1.5

	e1	e2	e3	e4	e5	e6	e7	e8	e9
P1	1	0	1	0	0	0	0	1	0
p2	1	0	0	1	0	0	0	0	1

Продолжение таблицы 1.5

P3	0	1	0	0	0	1	0	0	1
P4	0	1	0	1	1	0	0	0	1
P5	0	1	1	0	1	0	1	0	1
P6	0	1	1	0	0	0	1	0	1

1. 1.4 Числовые характеристики графа

1.5 Степени всех вершин графа

Степенью выхода вершины ориентированного графа называется число ребер, для которых эта вершина является началом (число ребер, «выходящих» из вершины). Степенью входа вершины ориентированного графа называется число ребер, для которых эта вершина является концом (число ребер, «входящих» в вершину).

Степени всех вершин графа на рисунке 1:

⁺(v₁)=2; ⁺(v₂)=2; ⁺(v₃)=2; ⁺(v₄)=2; ⁺(v₅)=1; ⁺(v₆)=0

^-(v₁)=0; ^-(v₂)=2; ^-(v₃)=1; ^-(v₄)=1; ^-(v₅)=3; ⁺(v₆)=2

1.6 Вершинная и реберная связность графа

Минимальное число вершин (ребер), удаление которых делает граф несвязным, называется вершинной (G) (реберной (G)) связностью графа G.

Вершинная и реберная связность графа на рис.1.1:

(G)=2

(G)=2

1.7 Цикломатическое число графа

Циклическое число определяется только для неориентированных графов. По варианту, дан ориентированный граф, то циклическое число находить не нужно.

1.8 Вершинное и реберное числа независимости

Множество S V графа G = (V, Г) называют внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для любого х S имеет место Гх S.

Множество внутренней устойчивости, содержащее наибольшее число элементов, называют наибольшим внутренне устойчивым множеством, а число элементов этого множества – числом внутренней устойчивости ₀(G) графа G (это число называют также вершинным числом независимости графа).

Два ребра графа называют смежными, если они инцидентны одной и той же вершине. Максимальное число попарно несмежных ребер графа называется его реберным числом независимости ₁(G).

Вершинное и реберное числа независимости графа на рисунке 1

₀(G)=2

₁(G)=3

1.9 Числа вершинного и реберного покрытий графа

Если ребро графа инцидентно его вершине, то говорят, что они покрывают друг друга. Множество вершин, покрывающих все ребра графа, называют вершинным покрытием графа G, а минимальную мощность этого множества - числом вершинного покрытия графа ₀(G). Аналогично, множество ребер, покрывающих все вершины графа, называют реберным покрытием графа G, а минимальную мощность этого множества – числом реберного покрытия графа ₁(G).

Числа вершинного и реберного покрытий графа на рисунке 1:

₀(G)=4

₁(G)=5

1.10 Вершинное и реберное число внешней устойчивости графа

Множество ТV графа G=(V, Г) называют внешне устойчивым, если любая вершина, не принадлежащая Т, соединена ребрами с вершинами из Т, т.е. для любого хТ имеет место ГхТ.

Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшим внешне устойчивым множеством, а число элементов этого множества – вершинным числом внешней устойчивости ₀(G) графа G.

Минимальная мощность множества ребер, покрывающих все ребра графа, называется реберным числом внешней устойчивости ₁(G) графа G.

Вершинное и реберное числа внешней устойчивости графа на рис.1.1:

₀(G)= 2

₁(G)= 2