Ряды Дирихле и их сходимость, гармонический ряд
Определение
1. Числовой ряд вида
называется рядом Дирихле с показателем
р,
R.
Заметим, что при
получаем ряд
,
который называется гармоническим.
Признаки сравнения рядов с положительными членами (док-во 1-го и 2-го признаков).
Теорема 1 (I
признак сравнения рядов с положительными
членами). Пусть даны 2 ряда с
положительными членами
и
.
Если,
начиная с некоторого номера N,
для всех
выполняется неравенство
,
тогда
1) из сходимости ряда следует сходимость ряда , 2) из расходимости ряда следует расходимость ряда .
Доказательство. На основании того,
что отбрасывание конечного числа членов
(свойство 1, лекция 1, разд. 1.3) не влияет
на сходимость или расходимость ряда,
можно считать, не
нарушая общности, что условие
выполнено для всех
.
Пусть
− частичная сумма ряда
,
а
− частичная сумма ряда
.
По условию
.
1) Если ряд
сходится,
то последовательность
ограничена сверху, а значит, ограничена
сверху и последовательность
.
Следовательно, по теореме 2 (лекция 1,
разд. 1.4) о необходимом и достаточном
условии сходимости ряда с положительными
членами ряд
сходится, так как существует конечный
предел последовательности
.
2) Если ряд расходится, то последовательность не ограничена, а значит, не ограничена и последовательность . Тогда по теореме 2 (лекция 1, разд. 1.4) ряд расходится. Теорема доказана.
Теорема 2 (предельный
признак сравнения рядов с положительными
членами). Даны 2 ряда с
положительными членами
и
и
пусть существует
,
тогда эти два ряда либо сходятся, либо
расходятся одновременно.
Доказательство. Так
как по условию
и
,
то согласно свойству предела
.
По условию
,
значит,
.
По определению предела для всех
существует окрестность
точки С такая, что
и существует такое натуральное число
,
зависящее
от
,
что для всех
выполняется неравенство
,
или
.
Если ряд
сходится, то сходится и ряд
(свойство 2, лекция 1, разд. 1.3), откуда
по I
признаку сравнения рядов следует
сходимость ряда
,
так как
.
Если же ряд
расходится, то расходится и ряд
,
а так как
,
то по I признаку сравнения
рядов ряд
также расходится. Теорема доказана.
Замечание. Если
,
или
,
то предельный признак не применим
(теорема 2 в этих случаях не верна).
Признак Даламбера (с док-вом).
Теорема 3 (признак Даламбера).
Пусть дан ряд с
положительными членами
,
и существует конечный предел
,
тогда:
1) ряд
сходится, если
,
2) ряд
расходится, если
,
3) если
,
то для выяснения сходимости ряда признак
Даламбера не применим.
Доказательство. 1) Пусть предел
существует и
.
Рассмотрим число q
такое, что
.
Из определения предела следует, что
существует
N,
начиная с которого
выполняется
неравенство
,
.
Таким образом,
,
т.е.
.
Берём n = N,
N+1, N+2,…,
тогда
,
,
,
…,
.
Запишем исходный ряд
в виде:
.
Рассмотрим новый ряд
. Этот ряд есть ряд геометрической
прогрессии с
и
,
который сходится, а значит, сходится
ряд
,
так как
на основании теоремы 1. Ряд
получен из исходного
отбрасыванием конечного
числа членов
,
тогда ряд
сходится (свойство 1, лекция 1, разд.
1.3). Таким образом, исходный ряд
сходится, если
.
Первая часть теоремы доказана.
2) Пусть
.
Рассмотрим число q
такое, что
.
,
из определения предела следует:
,
Таким
образом,
и при
общий член ряда
не стремится к 0, т.е. ряд
расходится, так как не выполняется
необходимое условие сходимости ряда
(теорема 1, лекция 1, разд. 1.3). Вторая часть
теоремы доказана.
3) Если
,
равен единице или не существует, в этом
случае для выяснения сходимости ряда признак Даламбера не применим.
Интегральный признак Коши (с док-вом).
Теорема 3 (интегральный признак Коши). Пусть дан ряд , члены которого удовлетворяют трём условиям:
а)
,
т.е. исходный ряд с положительными
членами;
б) члены ряда монотонно убывают,
т.е.
;
в) общий член ряда стремится к нулю: .
Пусть существует непрерывная,
монотонно убывающая, определённая при
функция f(x),
такая что
,
т.е.
.
Тогда, если несобственный интеграл
сходится, то ряд
тоже сходится; если
указанный интеграл расходится, то этот
ряд расходится.
Доказательство. Из условий теоремы
следует
при
.
Рассмотрим криволинейную трапецию,
ограниченную линиями
,
,
и
осью 0х (рис.1). Разобьём отрезок
точками
и рассмотрим n
криволинейных трапеций.
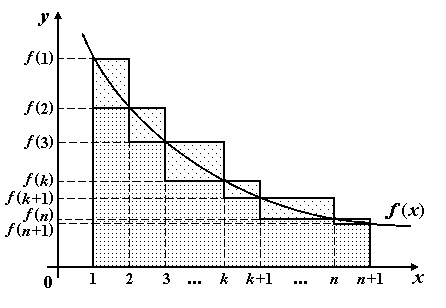
Рис. 1. Площадь криволинейной трапеции
Из геометрического смысла интеграла площадь криволинейной
трапеции
.
Заменим эту площадь суммой площадей n
прямоугольников с единичными основаниями:
,
,
причём
,
а
.
Из графика (рис. 1) следует:
,
т.е.
.
Рассмотрим два случая.
1) Пусть
сходится, т.е. имеет конечный предел
.
Так как
,
то
и
.
Итак, частичные суммы ряда ограничены
N,
тогда по теореме 2
(необходимый и достаточный признак
сходимости ряда с положительными
членами) ряд
сходится, значит, существует
.
2) Пусть интеграл
расходится, т.е.
неограниченно возрастает при
.
Тогда из неравенства
следует, что последовательность
неограниченно возрастает:
,
т.е. ряд расходится. Теорема доказана.
Замечание 1. Теорема остаётся верной
и тогда, когда её условия выполняются
не для всех членов ряда, а лишь начиная
с k-го (
),
в таком случае рассматривается интеграл
.
Замечание
2. Интегральный признак Коши существенно
облегчает исследование сходимости
ряда, так как позволяет свести этот
вопрос к выяснению сходимости интеграла
от удачно подобранной соответствующей
функции
,
что легко выполняется, применяя методы
интегрального исчисления.
Знакочередующиеся ряды: признак Лейбница (с док-вом).
Определение 1. Числовой ряд
,
где
,
называется знакочередующимся рядом.
Для установления сходимости таких рядов существует достаточный
признак сходимости, называемый признаком Лейбница.
Теорема 1 (признак Лейбница).
Пусть числовой ряд
удовлетворяет условиям:
1)
,
т.е. этот ряд знакочередующийся;
2) члены этого ряда монотонно убывают
по абсолютной величине:
т.е.
;
3) общий член ряда
стремится к 0, т.е.
.
Тогда ряд
сходится и его сумма
.
Доказательство.
1) Сначала рассмотрим частичную сумму
чётного порядка
и запишем её в виде:
.
В силу условия 2) теоремы 1 все выражения
в скобках положительны, тогда сумма
и последовательность
монотонно возрастает:
.
Теперь запишем эту сумму иначе:
.
В
последнем выражении каждое из выражений
в скобках положительно, поэтому
,
из чего следует, что последовательность
является ограниченной, и так как она
монотонно возрастает, то она сходится.
Другими словами существует
,
причём
.
2) Рассмотрим частичную сумму нечётного
порядка
,
которая положительна. Можно показать,
что последовательность
монотонно возрастает, так как монотонно
возрастает последовательность
и
.
Запишем выражение для
в виде:
,
так как все выражения в скобках
положительны, то
.
По условию 3) теоремы 1
,
тогда
,
откуда
.
Итак, при всех n
(чётных или
нечётных),
,
следовательно, исходный ряд сходится.
Теорема доказана.
Замечание 1. Признак Лейбница
можно также применять к рядам, для
которых условия теоремы выполняются с
некоторого номера
N.
Замечание
2. Условие 2) теоремы 1 (признак
Лейбница) о монотонности членов ряда
существенно.
Знакопеременные ряды: понятия абсолютной и условной сходимости, признак абсолютной сходимости, свойства абсолютно и условно сходящихся рядов.
Достаточный признак сходимости знакопеременных рядов
Числовой ряд
,
члены которого имеют произвольные знаки
(+), (−), называется знакопеременным
рядом. Рассмотренные выше знакочередующиеся
ряды являются частным случаем
знакопеременного ряда; понятно, что не
всякий знакопеременный ряд является
знакочередующимся. Например, ряд
− знакопеременный, но не являющийся
знакочередующимся рядом.
Отметим, что в знакопеременном ряде членов как со знаком (+), так и со знаком (−) бесконечно много. Если это не выполняется, например, ряд содержит конечное число отрицательных членов, то их можно отбросить и рассматривать ряд, составленный только из положительных членов, и наоборот.
Определение 1. Если числовой ряд
сходится и его сумма равна S,
а
частичная сумма равна Sn
, то
называется остатком ряда, причём
,
т.е. остаток сходящегося ряда стремится
к 0.
Рассмотрим сходящийся знакочередующийся ряд как частный случай знакопеременного ряда
,
где
.
Запишем его в виде
,
тогда по признаку Лейбница
;
так как
,
то
,
т.е. остаток сходящегося ряда стремится
к 0.
Для знакопеременных рядов вводятся понятия абсолютной и условной
сходимости.
Определение 2.
Ряд
называется сходящимся
абсолютно,
если сходится ряд, составленный из
абсолютных величин его членов
.
Определение 3. Если числовой ряд сходится, а ряд , составленный из абсолютных величин его членов, расходится, то исходный ряд называется условно (неабсолютно) сходящимся.
Теорема 2 (достаточный признак сходимости знакопеременных рядов). Знакопеременный ряд сходится, причём абсолютно, если сходится ряд, составленный из абсолютных величин его членов .
Доказательство. Обозначим через
частичную сумму ряда
:
,
а через
− частичную сумму ряда
:
.
Обозначим через
сумму всех положительных членов, а через
сумму абсолютных величин всех отрицательных
членов, входящих в
.
Очевидно, что
.
По условию теоремы ряд
сходится, тогда существует
,
и так как последовательность
− монотонно возрастающая и неотрицательная,
то
.
Очевидно, что
,
тогда последовательности
и
являются монотонно возрастающими и
ограниченными, причем их пределы равны
и
.
Тогда
.
Значит, исходный знакопеременный ряд
сходится
и сходится абсолютно. Теорема доказана.
Замечание. Теорема 2 даёт только
достаточное условие сходимости
знакопеременных рядов. Обратная теорема
неверна, т.е. если знакопеременный ряд
сходится, то не обязательно, что сходится
ряд, составленный из модулей
(он может быть как сходящимся, так и
расходящимся). Например, ряд
сходится по признаку Лейбница (см. пример
1 данной лекции), а ряд, составленный из
абсолютных величин его членов,
(гармонический ряд) расходится.
Степенные ряды: радиус, интервал, область сходимости. Свойства степенных рядов. Теорема Абеля (с док-вом).
Рассмотрим частный случай функционального
ряда, так называемый степенной ряд
,
где
.
Определение 3. Степенным рядом
называется функциональный ряд вида
,
где
− постоянные числа, называемые
коэффициентами
ряда.
Степенной ряд есть «бесконечный
многочлен», расположенный по возрастающим
степеням
.
Любой числовой ряд
является
частным случаем степенного ряда при
.
Рассмотрим частный случай степенного
ряда при
:
.
Выясним, какой вид имеет
область
сходимости данного ряда
.
Теорема 1 (теорема Абеля). 1) Если
степенной ряд
сходится в точке
,
то он абсолютно сходится при всяком х,
для которого справедливо неравенство
.
2) Если же степенной ряд расходится
при
,
то он расходится при всяком х, для
которого
.
Доказательство. 1) По условию степенной
ряд сходится в точке
,
т. е. сходится числовой ряд
(1)
и по необходимому признаку сходимости
его общий член стремится к 0, т.е.
.
Следовательно, существует такое число
,
что все члены ряда ограничены этим
числом:
.
Рассмотрим теперь любое х, для
которого
,
и составим ряд из абсолютных величин:
.
Запишем этот ряд в другом виде: так
как
,
то
(2).
Из неравенства
получаем
,
т.е. ряд
(3)
состоит из членов, которые больше
соответствующих членов ряда (2). Ряд
представляет собой сходящийся ряд
геометрической прогрессии со знаменателем
,
причём
,
так как
.
Следовательно, ряд (2) сходится при
.
Таким образом, степенной ряд
абсолютно сходится.
2) Пусть ряд расходится при , иными словами,
расходится числовой ряд
.
Докажем, что для любого х (
)
ряд расходится. Доказательство ведётся
от противного. Пусть при некотором
фиксированном
(
)
ряд сходится, тогда он сходится при всех
(см. первую часть данной теоремы), в
частности, при
,
что противоречит условию 2) теоремы 1.
Теорема доказана.
Следствие. Теорема Абеля позволяет
судить о расположении точки сходимости
степенного ряда. Если точка
является точкой сходимости степенного
ряда, то интервал
заполнен точками сходимости; если точкой
расходимости является точка
,
то
бесконечные интервалы
заполнены точками расходимости (рис.
1).
Рис. 1. Интервалы сходимости и расходимости ряда
Можно показать, что существует
такое число
,
что при всех
степенной ряд
абсолютно сходится, а при
− расходится. Будем считать, что если
ряд сходится только в одной точке 0, то
,
а если ряд сходится при всех
,
то
.
Определение 4. Интервалом
сходимости
степенного ряда
называется такой интервал
,
что при всех
этот ряд сходится и притом абсолютно,
а для всех х,
лежащих вне этого интервала, ряд
расходится. Число R
называется радиусом
сходимости
степенного ряда.
Замечание. На концах интервала вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.
Покажем один из способов определения интервала и радиуса сходимости степенного ряда.
Рассмотрим степенной ряд
и обозначим
.
Составим ряд из абсолютных величин его членов:
и применим к нему признак Даламбера.
Пусть существует
,
где
.
По признаку Даламбера ряд сходится,
если
,
и расходится, если
.
Отсюда ряд сходится при
,
тогда интервал сходимости:
.
При
ряд расходится, так как
.
Используя обозначение
,
получим формулу для определения радиуса
сходимости степенного ряда:
,
где
− коэффициенты степенного ряда.
Если окажется, что предел
,
то полагаем
.
Для определения
интервала и радиуса сходимости степенного
ряда также можно
использовать радикальный признак Коши,
радиус сходимости
ряда определяется из соотношения
.
Определение 5. Обобщенным степенным рядом называется ряд вида
.
Его также называют рядом по степеням
.
Для
такого ряда интервал сходимости имеет
вид:
,
где
− радиус сходимости.
Покажем, как находится радиус сходимости для обобщенного степенного ряда.
,
т.е.
,
где
.
Если
,
то
,
и область сходимости
R;
если
,
то
и область сходимости
.