Уравнение Бернулли
Определение. Дифференциальное уравнение вида
,
где
,
,
называется уравнением Бернулли.
Предполагая, что
,
разделим обе части уравнения Бернулли
на
.
В результате получим:
. (8.1)
Введём новую функцию
.
Тогда
.
Умножим обе части уравнения (8.1) на
и перейдем к функции z(x):
,
т.е. для функции z(x)
получили линейное неоднородное уравнение
1-го порядка. Это уравнение решается
методами, разобранными в предыдущем
разделе 1.7. Подставим в его общее
решение вместо z(x)
выражение
,
получим общий интеграл уравнения
Бернулли, который легко разрешается
относительно y. При
добавляется решение
.
Уравнение Бернулли можно также решать,
не делая перехода к линейному уравнению
путём подстановки
,
а применяя метод Бернулли, подробно
разобранный в 1.7. Рассмотрим применение
этого метода для решения уравнения
Бернулли на конкретном примере.
ДУ в полных дифференциалах. Формулировка аналитического признака полного дифференциала
Дифференциальные уравнения в полных дифференциалах
Определение. Если в уравнении
(9.1)
левая часть есть полный дифференциал
некоторой функции
,
то оно называется уравнением в полных
дифференциалах. Это уравнение можно
переписать в виде
,
следовательно, его общий интеграл есть
.
Например, уравнение
есть уравнение в полных дифференциалах,
так как его можно переписать в виде
.
А значит, общий интеграл задаётся
равенством
.
Теорема. Предположим, что функции M и N определены и непрерывны в некоторой односвязной области D и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда, для того чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество
. (9.2)
Доказательство. Доказательство необходимости этого условия очевидно. Поэтому докажем достаточность условия (9.2).
Покажем, что может быть найдена такая
функция
,
что
и
.
Действительно, поскольку
,
то
, (9.3)
где
– произвольная дифференцируемая
функция.
Продифференцируем равенство (9.3) по y:
.
Но
,
следовательно,
.
Положим
,
тогда
.
Итак, построена функция
,
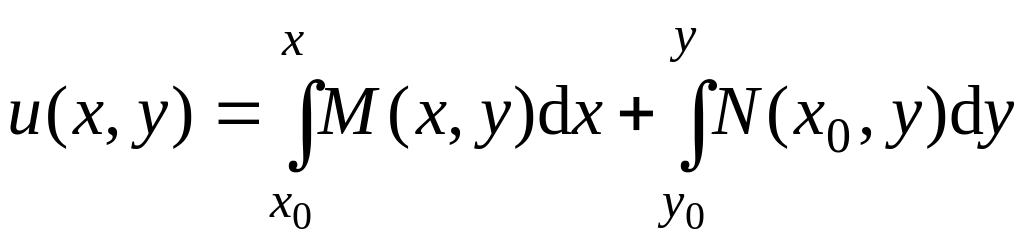для которой
,
а
.
Интегрирующий множитель. Достаточные условия существования интегрирующего множителя вида
(вывод).
Определение. Если уравнение
не является уравнением в полных
дифференциалах и существует функция
– такая, что после умножения на неё
обеих частей уравнения получающееся
дифференциальное уравнение
становится уравнением в полных
дифференциалах, т.е.
,
то функция
называется интегрирующим множителем
исходного уравнения.
В случае, когда уравнение является
уравнением в полных дифференциалах,
полагают
.
Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах.
Если µ есть непрерывно дифференцируемая функция от x и y, то имеем тождество:
.
Из этого тождества следует, что интегрирующий множитель µ удовлетворяет уравнению с частными производными 1-го порядка:
. (10.1)
Если заранее известно, что
,
где ω – заданная функция от x и y,
то уравнение (10.1) сводится к обыкновенному
(и притом линейному) уравнению с
неизвестной функцией µ от независимой
переменной ω:
, (10.2)
где
,
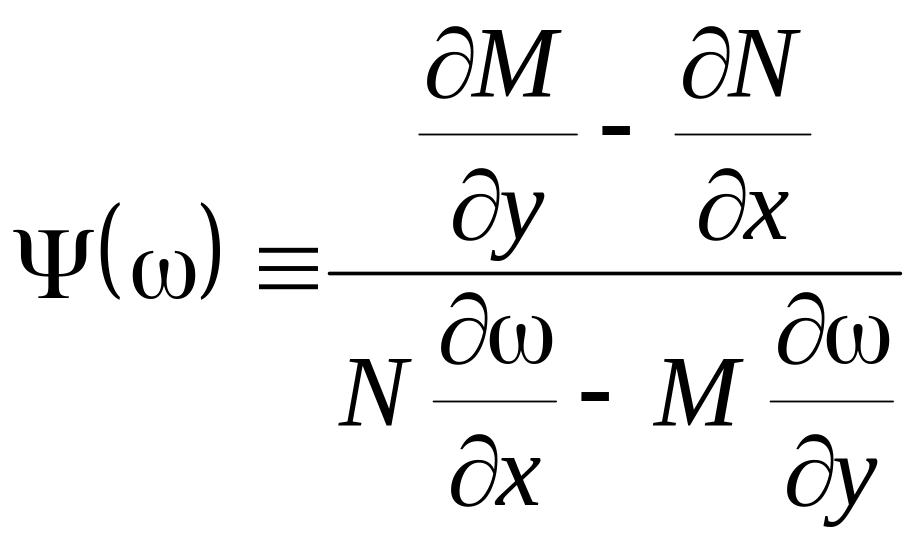т.е. указанная дробь является функцией только переменной ω.
Решая уравнение (10.2), находим интегрирующий множитель
,
.
В частности, уравнение
имеет интегрирующий множитель, зависящий
только от x (
)
или только от y (
),
если выполнены соответственно следующие
условия:
,
или
,
ДУ II-го порядка, допускающие понижение порядка.