Лаборатоные 2 семестр (паскаль) / 2 семестр / Монте Карло

Задание № 7

ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ

МОНТЕ-КАРЛО

Цель работы — знакомство с численными методами Монте-Карло, вычисление методом Монте-Карло кратного интеграла от заданной функции в выпуклой области.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим задачу вычисления n-мерного интеграла

в области V с границей Г, вложенной в n-мерный параллелепипед

W = [a_i  x_i  b_i; i = 1, 2, …, n},

имеющий объем



(7.1)

W = (b₁ – a₁)(b₂ – a₂) … (b_n – a_n).

Рис. 7.1. Область интегрирования

в случае двух переменных

На рис. 7.1 изображена область интегрирования V с границей Г, вложенная в прямоугольник W (n = 2).

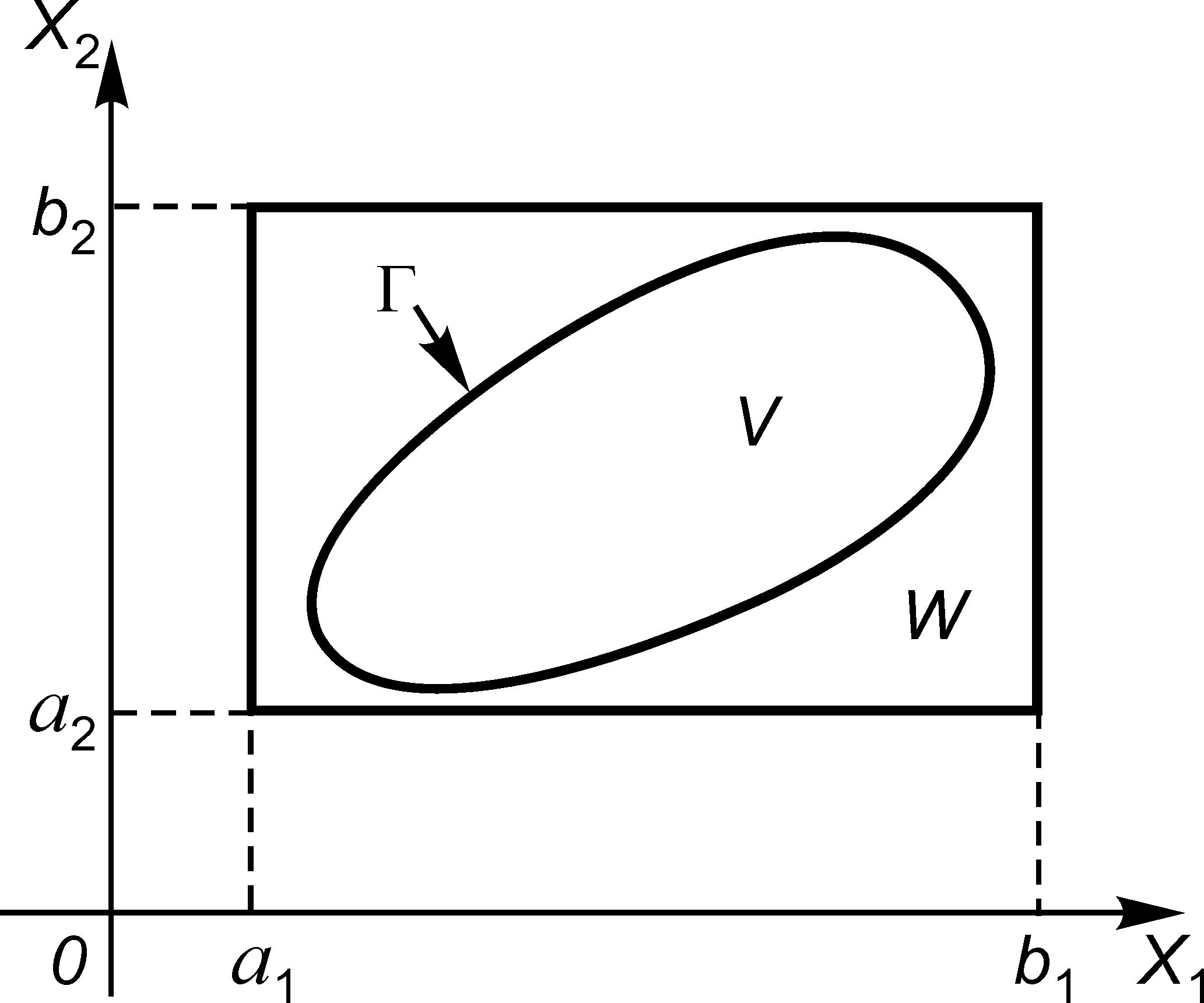
По теореме о среднем в интегральном исчислении среднее значение функции f(x) по области V дается равенством

(7.2)

где V — объем области V. Для вычисления с помощью генератора случайных чисел R, равновероятных на (0, 1), будем генерировать случайные точки X^(k) с координатами

равномерно распределенные в параллелепипеде W. Значение находится усреднением f(x) по точкам X^(k), принадлежащим области V:

где M — число точек X^(k), принадлежащих V.

Объем V области V можно приближенно оценить по формуле

где N — общее число случайных точек X^(k) в W, а W определяется формулой (7.1). Исходя из формулы (7.2) находим оценку интеграла I:

(7.3)

Принадлежность точки X^(k) области V можно устанавливать по заданной границе Г. Пусть, например, граница Г имеет уравнение

Г(x) = 0, и точки x, удовлетворяющие условию Г(x)  0, принадлежат области V. Тогда в сумму (7.3) следует включить все точки X^(k), удовлетворяющие условию

Г(X^(k))  0.

В теории вероятностей показано, что погрешность интегри­рования методом Монте-Карло имеет порядок О(N^-1/2), т.е. очень медленно убывает с ростом N. Тем не менее, при той же погрешности интегрирование методом Монте-Карло выполняет­ся на компьютере быстрее, чем другими методами уже при n>3, а при n>6 – это единственно приемлемый метод интегрирования.

ВАРИАНТЫ ЗАДАНИЙ

1. Методом Монте-Карло найти объемный заряд

в трехмерной области V, ограниченной эллипсоидом

с нормированной плотностью заряда .

ВАРИАНТЫ ФУНКЦИЙ

2. Температура Т в точках х=(х₁,х₂,x_з) шара

изменяется со временем t по закону

Найти среднюю температуру шара за время [t₁, t₂] по формуле

где - объём шара.

В качестве T(x,t) принять

где ρ(х) — одна из функции предыдущего задания, g₁=0.l ÷0.9

(i =1,2,3).

3. Вычислить объем |V| тела, ограниченного шестимерным эллипсоидом

Вычисление выполнить методом Монте-Карло по формуле

ПРОГРАММИРОВАНИЕ

Вычисление интеграла проведем для нескольких значений N, заданных отдельным массивом N (L) в головной программе. Соответственно, в программе следует организовать выдачи результатов по достижении числа случайных чисел очередного значения N из массива. Это даст возможность наблюдать за изменением результатов и сходимостью интегрирования с ростом N.

Блок-схема программы представлена на рис. 7.2. Основу программы составляет цикл (блоки 3-10) по l от l до L, где L —заданное число вариантов с различным количеством случайных чисел N_l, для которых осуществляется выдача результатов. В блоке 4 происходит обращение к датчику случайных чисел для вычисления ξ. На рисунке j — текущее число случайных точек, М — число случай­ных точек в области V, — оценки интеграла I и объема области V.

В качестве теста необходимо вычислить объём эллипсоида в трёхмерной области в соответствии с пунктом 3 задания. Известно аналитическое решение

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы подынтегральной функции и границы области

интегрирования для конкретного варианта;текст программы;

• значения интеграла для нескольких значений N, выбран-

ных в диапазоне N~ 10²- 10⁴.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие численные методы называются методами Монте- Кар-

ло?

2. Как вычисляются кратные интегралы методом Монте-Карло?

3. Как получена формула (7.3)?

4. Каков порядок погрешности интегрирования методом Монте-Карло?