Экстремумы функции

Определение 1. Точка   называется точкой максимума [точкой минимума] функции  , если существует такая  - окрестность   точки  , что для всех значений   из этой окрестности выполняется неравенство    .

Определение 2. Значение функции в точке максимума (точке минимума) называетсямаксимумом (минимумом) функции  .

Определение 3. Точки минимума и точки максимума называются точками экстремумафункции  , а значения функции в этих точках — экстремумами функции  .

Теорема 1. Если функция   непрерывна в точке  , а   на промежутке   и   на промежутке  , то   является точкой максимума функции  .

Теорема 2. Если функция   непрерывна в точке  , а   на промежутке   и   на промежутке  , то   — точка минимума функции  .

Теорема 3 (Ферма). Пусть функция   определена в некоторой окрестности точки   и дифференцируема в этой точке. Если   — точка экстремума функции  , то  .

Теорема 4. Пусть функция   дифференцируема в некоторой окрестности точки  , кроме, быть может, самой точки  , и непрерывна в точке  . Тогда, если   меняет знак с « » на « » (с « » на « ») при переходе через точку  , то   — точка минимума (точка максимума) функции  .

Экстремум функции Необходимое условие экстремума

      Функция g(x) в точке  имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки и для всех точек x  некоторой области:  , выполнено соответственно неравенство

(в случае максимума) или  (в случае минимума).

Экстремум функции находиться из условия: , если производная существует, т.е. приравниваем первую производную функции к нулю.

Достаточное условие экстремума

1) Первое достаточное условие:

Если:

а) f(x) непрерывная функция и определена в некоторой окрестности точки  такой, что первая  производная в данной точке равна нулю или не существует.

б) f(x) имеет конечную производную в окрестности задания и непрерывности функции

в) производная сохраняет определенный знак справа от точки  и слева от этой же точки, тогда точку  можно охарактеризовать следующим образом

     Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.

2) Второе достаточное условие

     Если функция g(x) обладает второй производной  причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если  , то точка является максимумом; если  , то точка является минимумом.

3) Третье достаточное условие

     Пусть функция g(x) имеет в некоторой окрестности точки   N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:

а) Если N - четно, то точка   экстремум функции:  у функции точка максимума,    у функции точка минимума.

б) Если N - нечетно, то в точке  у функции g(x) экстремума нет.

Теорема 1. (Теорема Ролля) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b);

3. на концах отрезка [a, b] принимает равные значения.

Тогда существует точка c  (a, b) такая, что f'(c) = 0.

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 118.

Геометрическая интерпретация теоремы Ролля

Из теоремы Ролля следует, что существует точка с  (a, b), в которой касательная к графику функции f(x) параллельна оси ОX (рис. 1).

Теорема 2. (Теорема Лагранжа) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с  (a, b) такая, что

 

f(b) − f(a) = f '(c) · (b − a) .

(1)

 

Формула (1) называется формулой Лагранжа, или формулой конечных приращений

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.

Геометрическая интерпретация теоремы Лагранжа

Представим формулу (1) в виде

 

f(b) − f(a) b − a    = f '(c) .

(2)

 

Число  

f(b) − f(a)

b − a

   есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке (c, f(c) ). Из формулы (2) следует, что существует точка с  (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.

Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.

    Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.

Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.

Будем в дальнейшем различать асимптоты вертикальные и наклонные.

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

Пусть при x→ x₀ с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е.   или   или  . Тогда из определения асимптоты следует, что прямая x = x₀ является асимптотой. Очевидно и обратное, если прямая x = x₀ является асимптотой, т. о.  .

Т аким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x₀ – 0 или x → x₀ + 0, x = x₀

Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x₀, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x₀.

Примеры.

1. Найти вертикальные асимптоты графика функции  .

Так как  , то прямая x = 2 является вертикальной асимптотой.

2. .

Прямая x = 0 – вертикальная асимптота.

НАКЛОННЫЕ АСИМПТОТЫ

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.

Т еорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда  . Аналогичное утверждение верно и при x → –∞.

Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию  . Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что  . Так как φ постоянный угол (φ ≠ π/2), то  , но

MN = MK – NK = y - y_ас = f(x) - (kx+b).

Следовательно, мы можем записать следующее равенство  .

Так как x → +∞, то должно выполняться равенство  . Но при постоянных k и b   и  . Следовательно,  , т.е.  .

Если число k уже известно, то  , поэтому  .

Для доказательства в случае x → –∞  все рассуждения аналогичны.

Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство  . Действительно

Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.

Сделаем несколько замечаний.

Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.

Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы

.

Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞  и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.

Примеры. Найти асимптоты кривых.

1. .

   1. Вертикальные:

x = 0 – вертикальная асимптота.

2. Наклонные:

.

При x → - ∞  получим те же значения k и b. Следовательно, прямая y = x + 2 является наклонной асимптотой.

2. y = e^–x sin x + x.

   1. Функция определена и непрерывна на всей числовой прямой, следовательно, вертикальных асимптот нет.

   2.  

а)  .

Итак, при x → +∞ наклонная асимптота у= х.

б)  , т. к.

, поэтому при x → - ∞  наклонных асимптот нет.

3. y = x – 2arctg x.

   1. Вертикальных асимптот нет.

   2.  

а)  .

. Наклонная асимптота y = x – π при  .

б)   при  .

Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность  типа   или  .  Пусть a является некоторым конечным действительным числом или равно бесконечности.

• Если   и  , то  ;

• Если   и  , то аналогично  .

• Вычислить предел  .

• Решение.

• Дифференцируя числитель и знаменатель, находим значение предела:

•       

• Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X, который является или всей областью определения функции или частью области определения. Сам интервал Xможет быть отрезком  , открытым интервалом  , бесконечным промежутком  . В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y = f(x). Кратко остановимся на основных определениях. Наибольшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  . 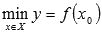Наименьшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  .