15. Определение коэффи­циента Пуассона и модуля продольной упругости. Метод электротензометрирования. Диаграмма напряжений.

Определение коэффициента Пуас­сона μ. Коэффициентом поперечной деформации или коэффициентом Пуассона называется отношение относительной поперечной деформации образца при растяжении (сжатии) ε' к отно­сительной продольной деформации ε, найденных в пределах пропорциональности:

(3)

Это отношение для каждого материала, в пределах упругости явля­ется величиной постоянной – упругой константой.

Для определения коэффициента поперечной деформации необхо­димо подвергнуть образец растяжению (или сжатию) в пределах пропорциональности, с измерениями продольных и поперечных его деформаций.

Испытание производится на образце прямоугольного поперечно­го сечения, который описан и использован при опытном определе­нии модуля упругости Е. Там же указывалась методика нахождения продольных деформаций такого образца. Для измере­ния поперечных деформаций при нагружении образца в соответствую­щем его направлении наклеиваются тензорезисторы. Их необходимо также располагать попарно на противоположных плоскостях образ­ца (рис. 4) с целью устранения влияния возможного малого его искривления и возможной внецентренности приложения нагруз­ки. При такой установке тензорезисторов можно, найдя попереч­ные деформации образца на противоположных плоскостях, привести их к деформации его по средней плоскости, взяв среднее арифме­тическое соответствующих деформаций, т.е.

где ε'₂, ε'₃ – относительные поперечные деформации на противопо­ложных плоскостях образца, полученные по показа­ниям тензорезисторов Т2 и ТЗ (рис. 4);

ε' – относительная поперечная деформация в средней плос­кости испытываемого образца.

По усредненному значению продольных ε_ср и поперечных ε'_ср деформаций, соответствующих интервалу нагружения образца, подсчитывается коэффициент Пуассона (3):

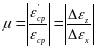
15. Геометрические характеристики плоских сечений. Статический момент. Определение центра тяжести плоской фигуры.

При расчетах элементов конструкций используются различные геометрические характеристики, а именно:

1) Площадь поперечного сечения (см2, мм2).

2) Статические моменты сечения (см3, мм3).

3) Осевые моменты инерции сечения (см4, мм4).

4) Полярные моменты инерции сечения (см4, мм4).

5) Центробежные моменты инерции (см4, мм4).

6) Осевые и полярные моменты сопротивления сечения (см3, мм3).

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):

Способы определения координат центра тяжести

Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

1 Аналитический (путем интегрирования).

2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3 Экспериментальный (метод подвешивания тела).

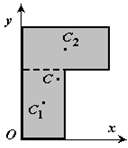
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C  и площадь  S известны. Например, проекцию тела на плоскость xOy  (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S₁  и  S₂ (S = S₁ + S₂). Центры тяжести этих фигур находятся в точках  C₁(x₁, y₁) и  C₂(x₂, y₂). Тогда координаты центра тяжести тела равны

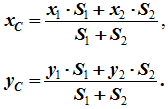
15. Моменты инерции и радиусы инерции плоской фигуры.

Осевой момент инерции фигуры - это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:

Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

Центробежный момент инерции фигуры - это интеграл произведений элементарных площадей на их расстояния до осей x и y:

Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4).

Осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести поперечного сечения стержня, называют собственными моментами инерции.

Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:

Формула радиуса инерции имеет вид:

Главным центральным осям инерции соответствуют главные радиусы инерции:

Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:

Для круглого сечения формула главных радиусов инерции имеет вид:

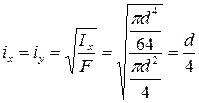
23. Главные и центральные оси инерции. Определение угла наклона главных центральных осей.

Можно найти положение двух взаимно перпендикулярных осей, при котором  . Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).

Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ей перпендикулярна).

Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями.

23. Виды расчетов на прочность.