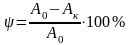6. Внутренние силы. Метод сечения.

Под действием внешней нагрузки любое реальное твердое тело изменяет свои размеры и форму, или деформируется, при этом порождая внутренние силы, противодействующие деформациям.

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.

Разрежем стержень, находящийся в равновесии под действием некоторой системы сил (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.

Отбросим одну из частей стержня и рассмотрим оставленную часть.

Иными словами, заменимдействие отброшенной части внутренними силами (рис. 1.3, б

6. Напряжения и деформации при растяжении (сжатии). Закон Гука.

Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины.

Растяжением (сжатием) называется такой вид деформации, когда в поперечном сечении стержня под действием внешних нагрузок возникает только один внутренний силовой фактор – продольная сила , а остальные внутренние силовые факторы отсутствуют.

Продольная сила вызывает нормальные напряжения , определяемые:

- при равномерном распределении их по сечению

- при неравномерном распределении

Продольная сила и напряжение положительны при растяжении и отрицательны при сжатии.

Для большинства конструкционных материалов между напряжением ( ) и продольной деформацией ( ) до определенного предела нагружения существует линейная зависимость

Закон Гука: Напряжение пропорционально деформации.

 Коэффициент пропорциональности (E) в формуле закона Гука  называется модуль продольной упругости или модуль Юнга модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). 

I форма. В поперечных сечениях бруса при центральном растяжении (сжатии) нормальные напряжения равны отношению продольной силы к площади поперечного сечения:

II форма. Относительная продольная деформация прямо пропорциональна нормальному напряжению , откуда .

6. Напряжения на косых площадках при растяжении.

Напряжения в наклонных площадках наблюдаются, если мысленно «разрезать» стержень, растягиваемый силами P, наклонной плоскостью под углом  к поперечному сечению

полное напряжение наклонного сечения в каждой точке будет равно:

где  – нормальное напряжение

11. Деформации при растяжении (сжатии). Абсолютное удлинение. Относительное удлинение (укорочение), коэффициент Пуассона

Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины

называется абсолютным удлинением стержня.

Отношение абсолютного удлинения стержня к его первоначальной длине называетсяотносительным удлинением (  – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:

При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:

.

Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:

Для различных материалов коэффициент Пуассона изменяется в пределах  . Например, для пробки  , для каучука  , для стали  , для золота  .

15. Правила построения эпюр при растяжении (сжатии). Правило знаков. Контроль правильности построения эпюр.

Эпюра – график, показывающий изменение какого-либо параметра по длине конструкции.

Эпюры дают наглядное представление о характере изменения силового фактора по длине или координате и позволяют установить местонахождение опасных сечений.

15. Экспериментальное определение механических характеристик при растяжении и сжатии.

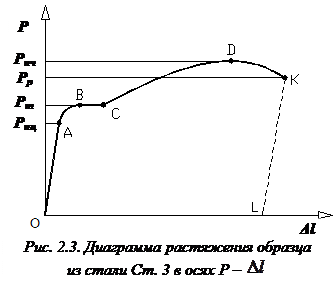
Испытание на растяжение является наиболее распространен­ным видом испытания материалов, так как при нем наиболее яр­ко выявляются характеристики прочности и пластичности мате­риалов.

При статических испытаниях на растяжение определяются следующие основные механические характеристики материалов:

_{предел пропорциональности} – σ_пц;

_{предел упругости} – σ_у;

_{предел текучести физический} — σ_т;

_{временное сопротивление} – σ_в;

_отно­сительное удлинение после разрыва – ε_;

_{относительное сужение} поперечного сечения после разрыва – ψ_;

истинный предел про­чности – σ_ист;

удельная работа, затраченная на разрыв – а.

Предел пропорциональности σ_пц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):

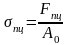
Предел упругости σ_у — напряжение, после которого появляется остаточное удлинение. В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу про­порциональности.

За­тем криволинейная часть диаграммы переходит в почти горизон­тальный участок — площадку текучести. Здесь деформации рас­тут практически без увеличения нагрузки (участок ВС).

Эти линии представляет собой следы смещения отдельных частиц материала, обусловленного большими деформациями образца. Они называются линиями Чернова

Предел текучести σ_т — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):

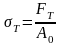
Временное сопротивление σ_в является основным показателем прочности материала и представляет собой наибольшее напряже­ние, которое выдерживает материал перед разрушением (МПа):

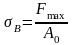
Относительное удлинение ε — отношение абсолютного удлине­ния к первоначальной длине, выраженное в процентах:

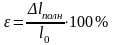(6)

Относительное сужение ψ — отношение уменьшения площади поперечного сечения образца после разрушения к первоначальной площади поперечного сечения, выраженное в процентах: