Предел на бесконечности по Коши
Пусть числовая функция
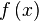задана
на множестве 
,
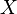в котором отыщется сколь угодно большой
элемент, то есть для всякого
положительного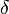 
в
нём найдётся элемент, лежащий за
границами отрезка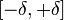 
.
В этом случае число
называется
пределом функции
на
бесконечности,
если для произвольного положительного
числа
отыщется
отвечающее ему положительное
число
такое,
что для всех точек, превышающих
по абсолютному
значению,
справедливо неравенство
.
Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий правее него. В этом случае число называется пределом функции на плюс бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих правее , справедливо неравенство .
Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий левее него. В этом случае число называется пределом функции на минус бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих левее
,
справедливо неравенство
.
30. Первый и второй замечательные пределы.
Первый замечательный предел:
Второй замечательный предел:
31. Непрерывность функции в точке на бесконечности. Теорема о непрерывных функциях.
Определение непрерывности функции в точке.
Функция f(x) называется непрерывной
в точке 
,
если предел слева равен пределу справа
и совпадает со значением функции в
точке
,
то есть 
.
Теоремы непрерывности
Теорема 1. Пусть функция f (x) непрерывна в точке x = a, и C является константой. Тогда функция Сf (x) также непрерывна при x = a. Теорема 2. Даны две функции f (x) и g (x), непрерывные в точке x = a. Тогда сумма этих функций f (x) + g (x) также непрерывна в точке x = a. Теорема 3. Предположим, что две функции f (x) и g (x) непрерывны в точке x = a. Тогда произведение этих функцийf (x) g (x) также непрерывно в точке x = a. Теорема 4.
Даны
две функции f (x) и g (x),
непрерывные при x
= a.
Тогда отношение этих функций 
также
непрерывно при x
= a при
условии, что 
.
Теорема
5.
Предположим,
что функция f (x) является
дифференцируемой в точке x
= a.
Тогда функция f (x) непрерывна
в этой точке (т.е. из дифференцируемости
следует непрерывность функции в точке;
обратное − неверно).
Теорема
6 (Теорема о предельном значении).
Если
функция f (x) непрерывна
на закрытом и ограниченном интервале [a,
b],
то она ограничена сверху и снизу на
данном интервале. Другими словами,
существуют числа m и M,
такие, что
для всех x в интервале [a, b] .
Теорема 7 (Теорема о промежуточном значении). Пусть функция f (x) непрерывна на закрытом и ограниченном интервале [a, b]. Тогда, если c − некоторое число, большее f (a) и меньшее f (b), то существует число x0, такое, что
32. Асимптоты графика функции. Вертикальная
Вертикальная
асимптота — прямая вида 
при
условии существования предела 
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.