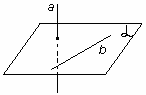
Случаи взаимного расположения прямых в пространстве.

рис. 14. Пересекающиеся прямые (лежат в одной плоскости).	рис. 15. Параллельные прямые (лежат в одной плоскости).	рис. 16. Скрещивающиеся прямые (не лежат в одной плоскости).

26. Уравнения плоскости в пространстве.

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0                                        

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

27. Поверхность второго порядка

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов  ,  ,  ,  ,  ,   отличен от нуля.

Типы поверхностей второго порядка

• 1.1 Цилиндрические поверхности

• 1.2 Конические поверхности

• 1.3 Поверхности вращения

• 1.4 Эллиптический параболоид

• 1.5 Гиперболический параболоид

• 1.6 Центральные поверхности

28. Предел числовой последовательности.

 Последовательность   - это функция, заданная на множестве натуральных чисел  . Число   называется пределом последовательности  , если для любого положительного числа  , как бы мало оно ни было, существует такой номер , что для всех   c номерами   справедливо неравенство  . Неравенство  , эквивалентное неравенству  , означает, что для любого  существует такой номер  , что все   c номерами  расположены между  и  . Последовательность, предел которой - конечное число  , называется сходящейся, и ее предел обозначают . Если изобразить элементы последовательности  на плоскости точками с координатами   , то неравенства  означают, что все точки   с номерами  расположены между параллельными оси абсцисс прямыми  и  .

Бесконечно малая последовательность. Последовательность   , предел которой равен нулю  , называется бесконечно малой.  

Бесконечно большая последовательность. Последовательность  называетсябесконечно большой, если для любого положительного числа   , как бы велико оно ни было, существует такой номер   , что для всех  с номерами справедливо неравенство   , записываем  .

29. Предел функции в точке и на бесконечности. Предел функции по Коши

Значение   называется пределом (предельным значением) функции   в точке  , если для любого наперёд взятого положительного числа   найдётся отвечающее ему положительное число   такое, что для всех аргументов  , удовлетворяющих условию  , выполняется неравенство  .^[1]