6. Взаимное расположение прямых. Угол между прямыми. Расстояние от точки до плоскости.

Угол между двумя прямыми

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Расстояние от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно:

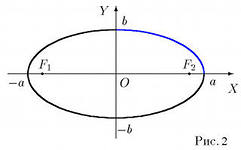
21. Эллипс: основные характеристики и изображения.

Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами  (постоянная величина).

Каноническое уравнение эллипса:

 

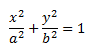
 Х и у принадлежат эллипсу.

а – большая полуось эллипса

b – малая полуось эллипса

У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса.

Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.

Если центры эллипса находятся не в центре С(α, β)

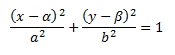
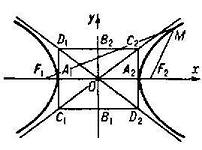
22. Гипербола: основные характеристики и изображения.

Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.

Каноническое уравнение гиперболы

 Гипербола имеет 2 оси симметрии:

а – действительная полуось симметрии

b – мнимая полуось симметрии

Ассимптоты гиперболы:

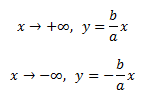
23. Окружность: основные характеристики и изображения.

Центр окружности – это геометрическое место точек в плоскости равностоящих от точки плоскости С(а,b).

Окружность задается следующим уравнением:

 

Где х,у – координаты произвольной точки окружности, R  - радиус окружности.

Признак уравнения окружности

1.       Отсутствует слагаемое с х,у

2.       Равны Коэффициенты при х² и у² 

24. Парабола: основные характеристики и изображения.

Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.

Каноническое уравнение параболы:

У²=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)

Если вершина параболы С (α, β), то уравнение параболы (у-β)²=2р(х-α)

Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х²=2qу

25. Уравнение прямой в пространстве. Взаимное расположение.

Систему называют общими уравнениями прямой в пространстве. Так как через любую прямую в пространстве проходит множество плоскостей, то любую прямую можно задать ее общими уравнениями и не единственным образом. 

(2) Уравнение и систему уравнений называют параметрическими уравнениями прямой в пространстве (в векторной и координатной форме соответственно). 

Уравнения называют каноническими уравнениями прямой в пространстве.

Уравнения называют уравнениями прямой, проходящей через две заданные точки   и  .