6. Определители их свойства. Решение систем линейных уравнений методом Крамера.

Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). 

Свойства определителей

1. Определитель не меняется при транспонировании.

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. Если в определителе переставить две строки, определитель поменяет знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a_{i j} = b_j + c_j (j= ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).

Рассмотрим систему уравнений 

На первом шаге вычислим определитель   , его называют главным определителем системы.

Если  , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если  , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:  и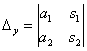 

На практике вышеуказанные определители также могут обозначаться латинской буквой  .

Корни уравнения находим по формулам: , 

6. Обратные матрицы. Матричный способ решения системы линейных уравнений.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Матричный способ!

  .

Решение.

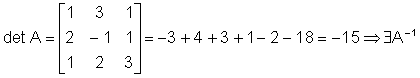
Найдем элементы союзной матрицы

Таким образом,

.

Проверка АА^-1 = Е. Действительно

6. Системы линейных алгебраических уравнений с п неизвестными. Решение систем линейных уравнений методом Гаусса.

Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида

Описание метода

Пусть исходная система выглядит следующим образом

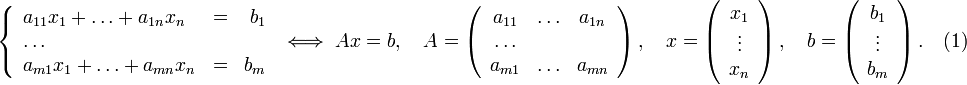
Матрица   называется основной матрицей системы,   — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

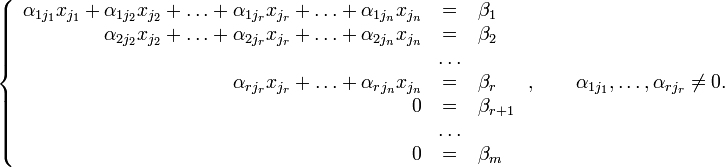
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  ^[3].

Тогда переменные   называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число  , где  , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.

Пусть   для любых  .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом   ( , где   — номер строки):

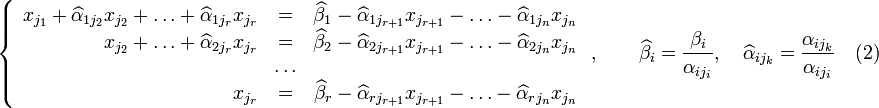, где 

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.