
- •§6. Однородные системы линейных алгебраических уравнений.
- •7.Определение скалярного произведения
- •8. Расстояние между двумя точками
- •2. Деление отрезка в данном отношении.
- •Полярная система координат.
- •11. Пучок прямых, уравнение пучка прямых.
- •12. Нормированное уравнение прямой. Расстояние от точки до прямой.
- •15. Парабола.
- •16. Линейные преобразования декартовых прямоугольных координат.
- •2. Вещественные числа и правило их сравнения.
- •19. Множества вещественных чисел, ограниченные сверху или снизу.
- •20. Числовые последовательности.
- •2. Ограниченные, неограниченные, бесконечно большие и бесконечно малые последовательности.
- •21. Монотонные последовательности.
- •23. Бесконечно малые и бесконечно большие функции.
Умножая
обе части равенства
 слева
на матрицу
слева
на матрицу
 ,
получим
,
получим

Равенство (3) определяет решение матричного уравнения (2).
Матрица
 является матрицей столбцом размера
является матрицей столбцом размера
 .
Записывая равенство (3) в развёрнутом
виде, т.е. приравнивая элементы в
одинаковых позициях. Мы найдём значения
.
Записывая равенство (3) в развёрнутом
виде, т.е. приравнивая элементы в
одинаковых позициях. Мы найдём значения
 .
Тем самым совместность системы (1)
доказана.
.
Тем самым совместность системы (1)
доказана.
Докажем теперь, что найденное решение является единственным решением системы (1).
Пусть
 – любое решение системы (1). Тогда матрица
столбец
– любое решение системы (1). Тогда матрица
столбец
 будет удовлетворять матричному
равенству
будет удовлетворять матричному
равенству Умножая
обе части равенства (4) слева на матрицу
,
получим
Умножая
обе части равенства (4) слева на матрицу
,
получим
 .Сопоставляя
равенства (3) и (5), приходим к выводу
.Сопоставляя
равенства (3) и (5), приходим к выводу
 что
доказывает единственность решения
системы (1).
что
доказывает единственность решения
системы (1).
Правило
Крамера. При
доказательстве теоремы 2.1 была получена
матричная форма записи решения системы
(1).
 .
Учитывая, что
.
Учитывая, что
 получим
получим
Следовательно Введём
следующие обозначения
Введём
следующие обозначения


Заметим,
что определители
 отличаются от определителя
только i-ым
столбцом. На месте i-го
столбца стоит столбец свободных членов
отличаются от определителя
только i-ым
столбцом. На месте i-го
столбца стоит столбец свободных членов
 .
.
Раскладывая
определитель
 по первому столбцу, определитель
по первому столбцу, определитель
 по второму столбцу и т.д. Определитель
по второму столбцу и т.д. Определитель
 по последнему столбцу, получим
по последнему столбцу, получим
Учитывая равенства (7) в равенствах (6) мы получим
 Формулы
(8) называются формулами Крамера.
Формулы
(8) называются формулами Крамера.
Элементарные преобразования системы линейных алгебраических уравнений.
Понятие
эквивалентной системы. Рассмотрим
две системы линейных алгебраических
уравнений с одинаковым количеством
неизвестных
 .
.

Заметим,
что числа
 могут не совпадать. Т.е. количество
уравнений системы (1) может не совпадать
с количеством уравнений системы (2).
могут не совпадать. Т.е. количество
уравнений системы (1) может не совпадать
с количеством уравнений системы (2).
Системы (1) и (2) с одинаковым количеством неизвестных называются эквивалентными, если каждое решение системы (1) является решением системы (2) и наоборот – каждое решение системы (2) является решением системы (1).
Элементарные преобразования системы. Элементарными преобразованиями системы называются преобразования следующих трёх типов.
Перестановка местами любых двух уравнений системы;
Умножение любого уравнения системы на любое отличное от нуля число;
Прибавление к одному уравнению системы другого её уравнения, умноженного на любое число.
Заметим, что элементарные преобразования системы означают элементарные преобразования сток её расширенной матрицы.
Теорема 3.1. Элементарные преобразования системы линейных алгебраических уравнений приводят её к эквивалентной системе.
Теорема
Кронекера-Капелли.Рассмотрим
систему
,
(1) ,где ,
,
 ,
,
 .
.
Теорема 5.1.(Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы.
Доказательство.
Пусть
 -
расширенная матрица системы (1).Матрицу
-
расширенная матрица системы (1).Матрицу
 путем элементарных преобразований
строк и перестановками столбцов можно
привести к матрице
путем элементарных преобразований
строк и перестановками столбцов можно
привести к матрице
 -
верхней трапециевидной формы. Применяя
эти преобразования к расширенной
матрице
,
получим систему
-
верхней трапециевидной формы. Применяя
эти преобразования к расширенной
матрице
,
получим систему
 (2)эквивалентную системе (1).
(2)эквивалентную системе (1).
 . (3)Заметим, что матрица неизвестных
. (3)Заметим, что матрица неизвестных
 может отличаться от матрицы
может отличаться от матрицы
 только
нумерацией неизвестных.
только
нумерацией неизвестных.
Система
(2) является системой с верхней
трапециевидной матрицей. В силу
результатов §4 главы 2, система (2)
совместна тогда и только тогда, когда
 .
(4)Заметим, что при выполнении равенства
(4), матрица
.
(4)Заметим, что при выполнении равенства
(4), матрица
 является
матрицей верхней трапециевидной формы,
полученной из матрицы
путем элементарных преобразований.
является
матрицей верхней трапециевидной формы,
полученной из матрицы
путем элементарных преобразований. .
(5)Из равенств (3), (4)и (5) следует, что
система (1) совместна тогда и только
тогда, когда
.
(5)Из равенств (3), (4)и (5) следует, что
система (1) совместна тогда и только
тогда, когда
 .
.
Метод Гаусса исследования и решения системы. Метод Гаусса исследования и решения системы уравнений состоит в приведении её к системе с верхней трапециевидной матрицей, и последующим исследованием и решением получившейся системы.
Теорема
5.2. (О структуре множества решений)
Любая система линейных алгебраических
уравнений c
основной матрицей
,
расширенной матрицей
и числом неизвестных
либо совместна и имеет единственное
решение ( ,
либо совместна и имеет бесконечное
множество решений (
,
либо совместна и имеет бесконечное
множество решений ( ,
либо не имеет ни одного решения (
,
либо не имеет ни одного решения ( .
.
Пример 1. Исследовать и решить систему
Р ешение.
Элементарными
преобразованиями строк расширенной
матрицы приведём матрицу системы к
верхней трапециевидной форме
ешение.
Элементарными
преобразованиями строк расширенной
матрицы приведём матрицу системы к
верхней трапециевидной форме
С истема
с последней расширенной матрицей
несовместна.
истема
с последней расширенной матрицей
несовместна.
§6. Однородные системы линейных алгебраических уравнений.
Рассмотрим
систему линейных алгебраических
уравнений  где
где
 ;
;
.
Система (1) называется однородной, если
;
;
.
Система (1) называется однородной, если
 и неоднородной, если хотя бы один из
свободных членов
и неоднородной, если хотя бы один из
свободных членов
 отличен от нуля. Рассмотрим однородную
систему
отличен от нуля. Рассмотрим однородную
систему
 (2)
;
(2)
;

 Из
теоремы Кронекера-Капелли следует, что
однородная система (2) всегда совместна,
так как ранг её расширенной матрицы
Из
теоремы Кронекера-Капелли следует, что
однородная система (2) всегда совместна,
так как ранг её расширенной матрицы
 ,
очевидно равен рангу матрицы
,
очевидно равен рангу матрицы
 Впрочем, это видно и непосредственно:
однородная система заведомо имеет
решение
Впрочем, это видно и непосредственно:
однородная система заведомо имеет
решение
 ,
называемое тривиальным решением.
,
называемое тривиальным решением.
Выясним, при каких условиях, система (2) имеет так же нетривиальное решение.
Теорема 6.1. Для того чтобы однородная система (2) с квадратной матрицей имела нетривиальное решение необходимо и достаточно, чтобы определитель матрицы равнялся нулю.
Доказательство.
Сначала
докажем необходимость. Пусть система
(2) имеет нетривиальное решение. Докажем,
что
 Предположим обратное, пусть
Предположим обратное, пусть
 .
Тогда по теореме система (2) имеет
единственное тривиальное решение, что
противоречит условию. Cледовательно
.
Тогда по теореме система (2) имеет
единственное тривиальное решение, что
противоречит условию. Cледовательно
 .
.
Докажем
теперь достаточность. Пусть
.
Тогда
 ,
где
расширенная матрица системы (2), а
-
число неизвестных. Тогда, согласно
теореме 5.2 главы 2, система (2) имеет
бесконечное множество решений, что
означает существование нетривиальных
решений.
,
где
расширенная матрица системы (2), а
-
число неизвестных. Тогда, согласно
теореме 5.2 главы 2, система (2) имеет
бесконечное множество решений, что
означает существование нетривиальных
решений.
6.Две
перпендикулярные оси на плоскости с
общим началом
 и одинаковой масштабной единицей
образуют декартову прямоугольную
систему координат на плоскости.
и одинаковой масштабной единицей
образуют декартову прямоугольную
систему координат на плоскости.
Понятие вектора и линейные операции над векторами.
Вектором
называется произвольный направленный
отрезок. Обознач.
 ,
где
– начало, а
конец данного направленного отрезка,
либо
,
где
– начало, а
конец данного направленного отрезка,
либо
 На чертеже изображается вектор стрелкой.
На чертеже изображается вектор стрелкой.![]() Начало вектора называется точкой его
приложения. Длина вектора
Начало вектора называется точкой его
приложения. Длина вектора
 или
или
 .
.
Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определённого направления и имеет длину равную нулю.
Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.
В се
нулевые векторы считаются равными.
се
нулевые векторы считаются равными.
Суммой
двух векторов
и называется вектор, идущий из начала
вектора
в конец вектора
при условии, что вектор
приложен
к концу вектора
.
называется вектор, идущий из начала
вектора
в конец вектора
при условии, что вектор
приложен
к концу вектора
.
Данное правило сложения двух векторов называется правилом треугольника.
 О
О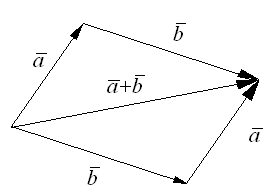 чевидно,
что этот же вектор
+
для
неколлинеарных векторов
чевидно,
что этот же вектор
+
для
неколлинеарных векторов
 может
быть получен, как диагональ параллелограмма,
построенного на векторах
может
быть получен, как диагональ параллелограмма,
построенного на векторах

Это правило сложения векторов называется правилом параллелограмма.
Правило сложения векторов обладает следующими свойствами:

 (Коммутативность
сложения)
(Коммутативность
сложения) (Ассоциативность
сложения)
(Ассоциативность
сложения)Существует нулевой вектор
 ,
такой что
,
такой что
 для любого вектора
.
для любого вектора
.
Для любого вектора существует противоположный к нему вектор
 ,
такой, что
,
такой, что
 .
.
Доказательство свойств 1 и 2 для неколлинеарных векторов проводится непосредственно построением. Свойство 3 очевидно.
Св-во
4.Очевидно, так как для любого вектора
 существует вектор
существует вектор
 ,
такой что
,
такой что
 .
Т.е.
.
Т.е. .
.
Разностью
векторов
и
называется такой вектор
 ,
что
,
что
 .
(
.
( .
)
.
)
Теорема
3.1.
Для любых векторов
существует
и притом единственная разность

Доказательство.
Рассмотрим
вектор
 .
Тогда
.
Тогда
 .
Следовательно существует разность
.
.
Следовательно существует разность
.
Докажем
единственность разности векторов
.
Пусть
 - разность векторов
,
тогда
- разность векторов
,
тогда
 Следовательно
если
- разность векторов
,
то
Следовательно
если
- разность векторов
,
то
 .
Единственность доказана.
.
Единственность доказана.
Замечание. Правило параллелограмма сложения неколлинеарных векторов позволяет построить и разность , как другую диагональ параллелограмма.
С войства
1 -4 позволяют распространить правило
сложения на сумму любого конечного
числа векторов.
войства
1 -4 позволяют распространить правило
сложения на сумму любого конечного
числа векторов.
Сумма
любого конечного числа векторов может
быть построена с помощью следующего
правила: если приложить вектор
 к концу вектора
к концу вектора
 ,
вектор
,
вектор
 к концу вектора
,
…, вектор
к концу вектора
,
…, вектор
 к концу вектора
к концу вектора
 ,
то сумма
,
то сумма
 представляет собой вектор, идущий из
начала вектора
к
концу вектора
.
представляет собой вектор, идущий из
начала вектора
к
концу вектора
.
Естественно
назвать это правило сложения векторов
правилом замыкания ломаной до
многоугольника. П роизведением
роизведением
 вектора
на
число
вектора
на
число
 называется вектор
называется вектор
 ,
коллинеарный вектору
,
имеющий длину
,
коллинеарный вектору
,
имеющий длину
 и направление, совпадающее с направлением
вектора
в случае
и направление, совпадающее с направлением
вектора
в случае
 и противоположное направлению
в
случае
и противоположное направлению
в
случае
 .
.
З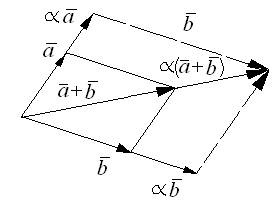 амечание.
В случае, когда
амечание.
В случае, когда
 ,
или
,
или
 произведение
представляет собой нулевой вектор,
направление которого не определено.
произведение
представляет собой нулевой вектор,
направление которого не определено.
Операция умножения вектора на число обладает следующими свойствами:
 ;
;

Свойства
5 – 7 доказываются одинаково. Приведём
доказательство свойства 5 для неколлинеарных
векторов и при условии
(случай
рассматривается аналогично). Приложим
векторы
в общую точку
 .
Построим вектор
.
Построим вектор
 ,
как диагональ параллелограмма,
построенного на векторах
.
Пусть
,
как диагональ параллелограмма,
построенного на векторах
.
Пусть
 - конец вектора
(
- конец вектора
( Т.к.
,
то векторы
Т.к.
,
то векторы
 и
(
и
( имеют одинаковые направления. Пусть
имеют одинаковые направления. Пусть
 - точка пересечения прямой
- точка пересечения прямой
 и прямой, проходящей через точку
,
параллельно вектору
.
и прямой, проходящей через точку
,
параллельно вектору
.
 - точка пересечения прямой
- точка пересечения прямой
 и прямой, проходящей через точку
параллельно вектору
.
Тогда четырёхугольник
и прямой, проходящей через точку
параллельно вектору
.
Тогда четырёхугольник
 является параллелограммом. Следовательно
является параллелограммом. Следовательно

С
другой стороны, из подобия треугольников
 ,
,
 и треугольников
и треугольников
 следует, что
следует, что Из
равенств (2) и (3) следует, что
Из
равенств (2) и (3) следует, что
 ,
,
 .
Т.к.
.
Т.к.
 и
имеют
одинаковые направления, получим
и
имеют
одинаковые направления, получим
 Аналогично
Аналогично
 .
Учитывая полученные выражения
.
Учитывая полученные выражения
 ,
найдем
,
найдем
 .
.
Проекция вектора на ось и её свойства.
Пусть
дан произвольный вектор
.
Пусть
 - произвольная ось. Обозначим через
- произвольная ось. Обозначим через
 основания перпендикуляров, опущенных
на ось
из точек
основания перпендикуляров, опущенных
на ось
из точек
 соответственно.
соответственно.
Проекцией
вектора называется
величина
называется
величина
 .
Рис.
.
Рис.
Углом
наклона вектора
 к оси
называется угол между двумя лучами,
выходящими из произвольной точки
к оси
называется угол между двумя лучами,
выходящими из произвольной точки
 ,
один из которых имеет направление,
совпадающее с направлением вектора
,
а другой – направление, совпадающее с
направлением оси
.
,
один из которых имеет направление,
совпадающее с направлением вектора
,
а другой – направление, совпадающее с
направлением оси
.
Теорема 4.1. Проекция вектора на ось равна произведению длины вектора на косинус угла наклона вектора к оси .
Доказательство.
Пусть
 – ось, проходящая через начало
вектора
и
имеющая то же направление, что и ось
.
Пусть
– ось, проходящая через начало
вектора
и
имеющая то же направление, что и ось
.
Пусть
 – основание перпендикуляра, опущенного
из точки
на ось
.
- основания перпендикуляров, опущенных
из точек
соответственно на ось
.
Тогда
– основание перпендикуляра, опущенного
из точки
на ось
.
- основания перпендикуляров, опущенных
из точек
соответственно на ось
.
Тогда
 ,
где
,
где
 - величина направленного отрезка
- величина направленного отрезка
 .
.

Возможны
два случая. 1. Направленный отрезок
 имеет направление, совпадающее с
направлением оси
.
(рис.2)
имеет направление, совпадающее с
направлением оси
.
(рис.2)
2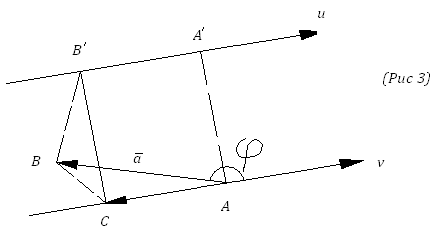 .
Направленный отрезок
имеет направление противоположное к
направлению оси
.
.
Направленный отрезок
имеет направление противоположное к
направлению оси
.
Заметим,
что в первом случае (рис 2)
 – угол наклона вектора
к оси
будет острым, во втором случае (рис 3)
тупым.
– угол наклона вектора
к оси
будет острым, во втором случае (рис 3)
тупым.
Рассмотрим случай 1.
Для
рассматриваемого случая имеем
 .
Четырехугольник
.
Четырехугольник
 является
прямоугольником. Поэтому
является
прямоугольником. Поэтому
 .Из
прямоугольного треугольника
.Из
прямоугольного треугольника
 имеем
имеем Так
как, по определению
Так
как, по определению
 ,
из равенств (2), (3), (4) находим
,
из равенств (2), (3), (4) находим
Тем самым, для случая 1 теорема доказана. Случай 2 рассматривается аналогично.
Рассмотрим
декартову прямоугольную систему
координат
 с началом в точке
и тройку векторов
с началом в точке
и тройку векторов
 единичной длины, приложенных к точке
,
имеющих направления, совпадающие с
направлениями этих осей соответственно.
единичной длины, приложенных к точке
,
имеющих направления, совпадающие с
направлениями этих осей соответственно.
Теорема
4.2. Для
любого вектора
 существует единственная тройка чисел
существует единственная тройка чисел
 такая, что
такая, что

при
этом
 ,
,
 ,
,
 .
.
Доказательство.
Приложим
вектор
в
точке
и проведём через его конец
 плоскости, параллельные координатным
плоскостям
плоскости, параллельные координатным
плоскостям
 .
Точки пересечения этих плоскостей с
осями
.
Точки пересечения этих плоскостей с
осями
 обозначим соответственно
обозначим соответственно
 .
.
О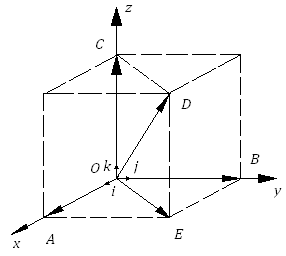 чевидно,
что
чевидно,
что
 .
Т.к.
.
Т.к.
 ,
мы находим
,
мы находим
 .
Из определения величины
и из того, что
.
Из определения величины
и из того, что
 следует, что
следует, что
 .
Так как проекция вектора на ось
.
Так как проекция вектора на ось
 по определению есть величина
,
то из последнего равенства получим
по определению есть величина
,
то из последнего равенства получим
 .
Аналогично доказывается справедливость
следующих равенств:
.
Аналогично доказывается справедливость
следующих равенств:
 =
= =
= .
Учитывая эти равенства в равенстве (6),
найдем
=
.
Учитывая эти равенства в равенстве (6),
найдем
= +
+ +
.
(7)
+
.
(7)
Введем
обозначения


 ,
запишем равенство (7) в
,
запишем равенство (7) в

Единственность легко получить с помощью геометрических рассуждений.
Числа
 ,
,
 в равенстве (5) называются координатами
вектора
в равенстве (5) называются координатами
вектора
 Тот факт, что
являются координатами вектора
,
обозначается следующим образом:
Тот факт, что
являются координатами вектора
,
обозначается следующим образом:
 .
.
Теорема
4.3.
Пусть в прямоугольной системе координат
даны произвольные две точки
 ,
,
 .Тогда
координаты
.Тогда
координаты
 вектора
вектора
 соответственно равны
соответственно равны
Доказательство.
Обозначим через
 и
и
 основания перпендикуляров, опущенных
из точек
на ось
.
Тогда по определению
основания перпендикуляров, опущенных
из точек
на ось
.
Тогда по определению
 ,
,
 ,
где
,
где
 – величины направленных отрезков
– величины направленных отрезков
 и
и

 величина
направленного отрезка
величина
направленного отрезка равна
равна
 .
С другой стороны величина
является проекцией вектора
на ось
.
С другой стороны величина
является проекцией вектора
на ось
 .
Следовательно
является координатой
.
Следовательно
является координатой
 вектора
.
Аналогично доказывается равенство
вектора
.
Аналогично доказывается равенство
 и
и
 .
.
Замечание.
Если
точки
 и
и
 расположены в плоскости
расположены в плоскости
 ,
то для координат вектора
,
то для координат вектора справедливы равенства
справедливы равенства
 и
.
и
.
Теорема
4.4. При
сложении двух векторов и
и
 их
координаты складываются. При умножении
вектора
на любое число 𝜆
все его координаты умножаются на это
число.
их
координаты складываются. При умножении
вектора
на любое число 𝜆
все его координаты умножаются на это
число.
Доказательство.
Пусть
 ,
,
 .
Складывая эти равенства и пользуясь
свойствами линейных операций, получим
.
Складывая эти равенства и пользуясь
свойствами линейных операций, получим
 .Из
последних равенств вытекает утверждение
теоремы.
.Из
последних равенств вытекает утверждение
теоремы.
Теорема 4.5. При сложении двух векторов и их проекции на произвольную ось складываются. А при умножении вектора на любое число 𝜆 его проекция на произвольную ось умножается на число 𝜆.
Доказательство. Пусть даны произвольные векторы , и ось . Введём декартову прямоугольную систему координат так, чтобы ось совпадала с осью .
Пусть
в введённой системе координат
 ,
,
 .
Тогда в силу теоремы 4.4
.
Тогда в силу теоремы 4.4
 и
и
 .
.
Следовательно
 и
и Теорема
доказана.
Теорема
доказана.
