7) Следы прямых и плоскостей.

Прямых:

След прямой – точка пересечения прямой с соответствующей плоскостью проекции.

Для построения фронтального следа прямой продолжаем горизонтальную проекцию прямой до пересечения с осью ОХ и восстанавливаем перпендикуляр к оси до пересечения с фронтальной проекцией прямой. С помощью этих правил на рис. 2.18 и рис. 2.19 построены следы прямых а и b.

Так как следы прямых – точки, в которых прямая переходит из одной четверти в другую, то они позволяют определить видимость этой прямой.

Та часть прямой, которая расположена в пределах первого октанта, будет видимой. Проекции видимой части прямой изображаются сплошными линиями, а невидимой – штриховыми.

Плоскостей:

Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости  (АВС). Фронтальный след плоскости 2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости. Горизонтальный след1 – прямая, проходящая через горизонтальный след прямой АВ и x. Профильный след3 – прямая соединяющая точки (y и z) пересечения горизонтального и фронтального следов с осями.

8) Пересечение прямой с пл. Частного и общего положения.

Чтобы определить точку пересечения прямой m с плоскостью, заданной треугольником АВС, необходимо выполнить следующее:

- провести через прямую m фронтально-проецирующую плоскость Р (Р2);

- определить линию пересечения плоскости Р и треугольника АВС 12 (1222 и 1121);

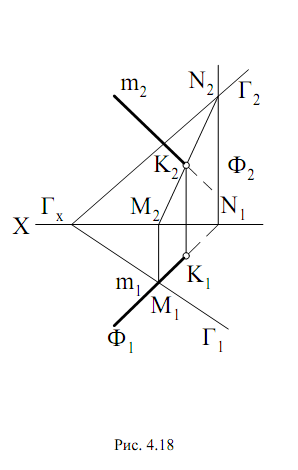- определить точку пересечения прямой m (m1, m2) с треугольником АВС. Эта точка находится на линии пересечения плоскостей Р и треугольника АВС – 12 (1121 и 1222). Сначала определяем горизонтальную проекцию К1, а затем фронтальную К2.

При определении точки пересечения прямой m с плоскостью, заданной следами Г1 и Г2 (рис. 4.18), необходимо также прямую m заключить в горизонтально-проецирующую плоскость Ф (Ф1 и Ф2) и найти их линию

пересечения MN (M1N1 и M2N2). Фронтальная проекция точки пересечения прямой К2 будет находиться на фронтальной проекции линии пересечения

M2N2, горизонтальная проекция К1 находится при помощи линии связи.

9) Пересечение плоскостей общего положения.

Точка N является фронтальным следом линии пересечения плоскостей, а точка М – горизонтальным следом линии пересечения. Одновременно в этих точках находятся и соответствующие проекции этих следов

N2 и M1. Так как точка N2 находится во фронтальной плоскости проекций, то горизонтальная проекция N1 будет находиться на оси Х. Аналогично и с точкой М (М1 и М2). Соединяя прямыми линиями одноименные проекции

точек М1 с N1 и М2 с N2, получим проекции прямой MN – линии пересечения плоскостей Г и Р.