
- •1)Проецирование точки на 2 и 3 взаимноперп.Пл. Проекций.
- •2) Прямая. Классификация прямых
- •3) Определение н.В. Прямых и углов наклона к пл-ям проекций
- •4) Пл. Общего и частного положения.
- •5) Главные линии плоскости.
- •6) Определение углов наклона пл. К плоскостям проекций.
- •7) Следы прямых и плоскостей.
- •8) Пересечение прямой с пл. Частного и общего положения.
- •9) Пересечение плоскостей общего положения.
- •1 0) Прямые перпендикулярные к плоскости. Перпендикулярность плоскостей.
1)Проецирование точки на 2 и 3 взаимноперп.Пл. Проекций.
Методы проецирования:
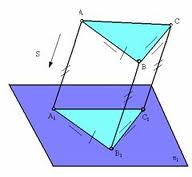
1.Метод центрального проецирования
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S - центра проецирования.

2.Метод параллельного проецирования
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S.

3.Метод ортогонального проецирования
Ортогональное проецирование - это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
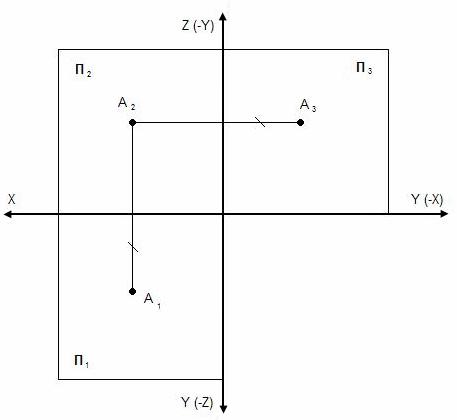
Проецирование точки на 3 плоскости проекций
Эпюр Монжа
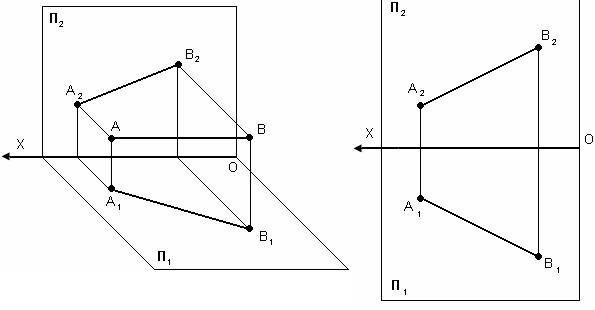
2) Прямая. Классификация прямых
В зависимости расположения прямой относительно плоскости проекции прямая может быть:
1.Общего положения – прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.
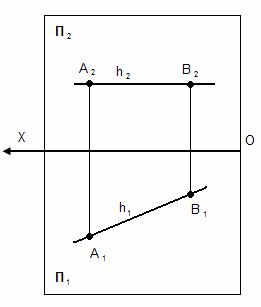
2.Прямые частного положения:
а)прямая уровня – прямая параллельная одной из плоскостей проекций(гор.,фр.,пр.).

б)проецирующая прямая – прямая, перпендикулярная к одной из плоскостей проекции(гор., фр., пр.).
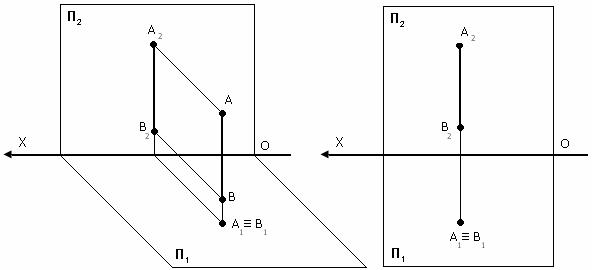
Точка принадлежит прямой, если проекции точки принадлежат одноименным проекциям прямой.
3) Определение н.В. Прямых и углов наклона к пл-ям проекций
Решить такие задачи можно несколькими способами: способом прямоугольного треугольника, способом вращения, заменой плоскостей проекций.
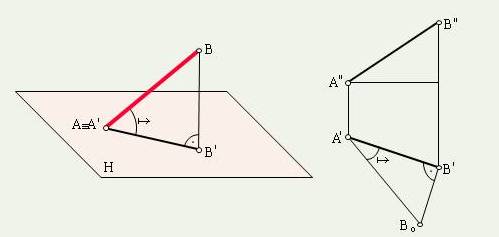
Рассмотрим способ прямоугольного треугольника:
Возьмем отрезок АВ и построим его ортогональнаю проекцию на горизонтальной плоскости проекций H. В пространстве при этом образуется прямоугольный треугольник A'BB', в котором одним катетом является горизонтальная проекция этого отрезка, вторым катетом разность высот точек А и В отрезка, а гипотенузой является сам отрезок. На чертеже прямоугольный треугольник построен на горизонтальной проекции отрезка АВ, второй катет треугольника B'Bo равен разности высот точек АВ, замеренную на плоскости V, гипотенуза его и будет натуральной величиной отрезка АВ. Угол между горизонтальной проекцией A'B' и гипотенузой A'Bo треугольника A'В'Bo это угол наклона данного отрезка AB к плоскости H. Аналогичное построение можно сделать на фронтальной проекции отрезка , только в качестве второго катета надо взять разность глубин его концов, замеренную на плоскости H.
4) Пл. Общего и частного положения.
Классификация плоскостей:
В зависимости от положения плоскости относительно плоскостей проекций, плоскости могут быть:
1.плоскостью общего положения
Плоскость, наклоненная ко всем трем плоскостям проекций, называется плоскостью общего положения.
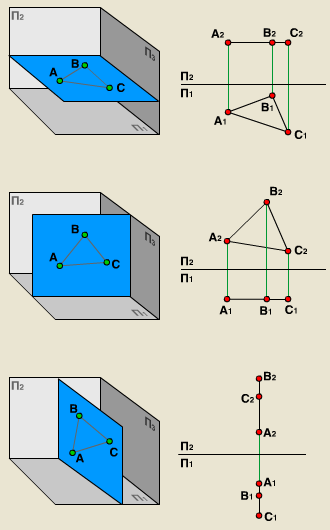
2.плоскостью частного положения:
а)уровня – плоскость параллельная одной из плоскостей проекций.
Горизонтальная плоскость уровня - || П1
Фронтальная плоскость уровня - || П2
Профильная плоскость уровня - || П3
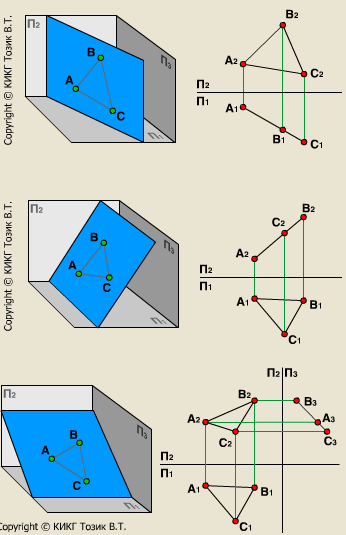
б)проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций.
Горизонтально-проецирующая плоскость
Фронтально-проецирующая плоскость
Профильно-проецирующая плоскость
Плоскость может быть задана:
а)тремя точками, не лежащие на одной прямой;
б)двумя параллельными прямыми;
в)одной прямой и точкой;
г)двумя пересекающимися прямыми;
д)следами.
