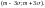- •Случайные события и их классификация.
- •Классическое определение вероятности.
- •Аксиоматическое определение вероятности. Геометрическое определение вероятности.
- •Условная вероятность. Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Байеса.
- •Наивероятнейшее число наступлений события.
- •Локальная теорема Муавра – Лапласа
- •Интегральная теорема Лапласа.
- •Функция распределения случайной величины и ее свойства.
- •Дискретные случайные величины.
- •Плотность распределения вероятностей и ее свойства.
- •Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
- •Дисперсия случайной величины и ее свойства.
- •Биноминальный закон распределения. Математическое ожидание и дисперсия случайной, величины распределенной по биноминальному закону.
- •Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.
- •Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
- •Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
- •Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
- •Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
- •Корреляционный момент и коэффициент корреляции и их свойства.
- •Моменты случайной величины. Ассиметрия и эксцесс.
- •Неравенство Маркова и Чебышева.
- •Закон больших чисел « в форме» теоремы Чебышева.
- •Теорема Бернулли.
- •Понятие о «центральная предельная теорема». Теорема Ляпунова.
- •Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.
- •Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.
- •Выборочный метод. Точечное оценивание.
- •Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
- •Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
- •Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
- •Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.
- •Критерий Пирсона.
- •Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.
- •Критерий согласия Колмогорова.
- •Однофакторный дисперсионный анализ.
- •Модели и основные понятия корреляционного и регрессионного анализа.
- •Линейная корреляционная зависимость и прямые регрессии.
- •Коэффициент линейной корреляции и его свойства.
- •Понятие «нелинейная корреляция».
- •Анализ соответствия регрессионной модели наблюденным данным.
Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
Равномерное
распределение: Пусть
плотность вероятности равна нулю всюду,
кроме отрезка
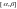 ,
на котором все значения случайной
величины Х одинаково возможны. Выражение
плотности распределения вероятностей
,
на котором все значения случайной
величины Х одинаково возможны. Выражение
плотности распределения вероятностей
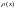 имеет
следующий вид:
имеет
следующий вид:
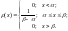
Функция
равномерного распределения задается
формулой:

Математическое
ожидание, дисперсия и среднее
квадратическое отклонение соответственно
равны:

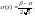
Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
Показательное
распределение.
Показательным (экспоненциальным)
называют распределение вероятностей
непрерывной случайной величины
,
которое описывается функцией плотности
вероятности:
 где
где
 постоянная и называется параметром
экспоненциального распределения.
постоянная и называется параметром
экспоненциального распределения.
Функция
распределения случайной величины,
распределенной по показательному
закону, имеет вид:

Математическое
ожидание
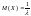 .
Дисперсия
.
Дисперсия
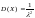 ,
среднее квадратическое отклонение
,
среднее квадратическое отклонение
 .
.
Условия возникновения: СВ Х – интервал времени между 2 соседними событиями в простейшем или Пуассоновском процессе/потоке СС, λ – интенсивность потока.
Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
Распределение с
непрерывной случайной величины
называется нормальным, если плотность
распределения ее описывается формулой: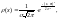 где
где
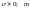 - параметры распределения.
- параметры распределения.
Функция распределения случайной величины Х, распределенной по нормальному закону:

Полученный интеграл
нельзя выразить через элементарные
функции, но его можно вычислить через
специальную функцию:
 ,
называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и
,
называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и

Математическое
ожидание и дисперсия соответственно
равны
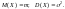
Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
Функция распределения случайной величины Х, распределенной по нормальному закону:

Полученный интеграл
нельзя выразить через элементарные
функции, но его можно вычислить через
специальную функцию:
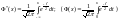 ,
называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и
,
называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и

Вероятность
попадания случайной величины
 ,
подчиненной нормальному закону
распределения, на заданный интервал
,
подчиненной нормальному закону
распределения, на заданный интервал
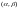 ,
определяется следующим образом:
,
определяется следующим образом:
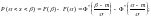 или
или
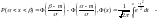 функция Лапласа.
функция Лапласа.
Вероятность заданного отклонения вычисляется по формуле:
 или
или
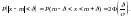
Интервалом
практически возможных значений
случайной величины
,
распределенной по нормальному закону,
будет интервал