7. Формула полной вероятности. Формула Байеса.

Пусть случайный эксперимент можно описать событиями 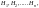которые являются попарно несовместными и Такие события называют гипотезами . Предполагается, что событие может произойти с одной из гипотез .

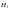Теорема: Вероятность любого события , которое может произойти с одной из гипотез будет равна сумме произведений вероятностей гипотез на условную вероятность события : 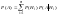- формула полной вероятности.

Пусть случайный эксперимент можно описать попарно несовместными событиями 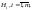объединение которых образует пространство элементарных событий 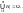Событие может произойти с одной из гипотез. Предполагается, что в результате эксперимента произошло событие . Как изменится вероятность гипотез при этом? Ответ на поставленный вопрос дает следующая теорема.

Теорема: Пусть событие может произойти с одной из гипотез которые описывают случайный эксперимент. Если в результате реализации эксперимента произошло событие , то вероятность гипотез вычисляются по следующим формулам :

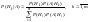- формулы Байеса.

8. Повторные независимые испытания. Формула Бернулли.

Пусть проводиться n независимых одинаковых опытов, в каждом из которых событие А появляется с вероятностью р. Вероятность того, что событие А произойдет ровно в к опытах из n испытаний, вычисляется по формуле Бернулли: , где q=1-p, вероятность того, что событие А не появится в 1 опыте.

Свойства формулы Бернулли:

1. Правая часть формулы представляет собой общий член разложения бинома Ньютона: .

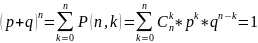2. Число k0, которому соответствует max вероятность P(n, k0) называется наивероятнейшим числом появления события А и определяется по формуле: .

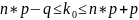3. Вероятность, что в n испытаниях событие А появится хотя бы 1 раз =:.

9. Наивероятнейшее число наступлений события.

Вычисление вероятности P(n,k) при больших значениях числа n по формуле Бернулли проблематично. Поэтому вычисление соответствующих вероятностей проводится с помощью приближенных формул.

Если количество испытаний велико n-> ∞, а вероятность наступления события мало р->0, так что n*p->a, где 0<a<∞ и вероятность намного меньше, чем 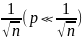, то используется формула Пуассона (предельная для формулы Бернулли): 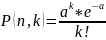, где a=n*p.

10. Локальная теорема Муавра – Лапласа

В случае, если число испытаний велико (n>>20, p>0,1) и интересующее нас событие наступает ровно л раз применяется локальная теорема Муавра-Лапласа. Вероятность вычисляется по формуле, где 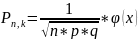, где φ(х) – функция Гаусса, которая имеет табулированное значение, .

Функция φ(х) является четной, аргумент 0≤х≤3,999… При значениях больших указанных в области определения функция принимает значение 0.

11. Интегральная теорема Лапласа.

При условии, что n>>20, p>0,1 и интересующее нас событие наступает от к1 до к2 раз, применяется интегральная теорема Муавра-Лапласа.

Вероятность: 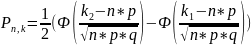, где Ф(х) – табулированная функция Лапласа.

Свойства функции Ф(х):

- нечетная: Ф(-х)=-Ф(х);

- для аргумента функции 0≤х≤5 значения функции находятся по таблице;

- при х≥5 Ф(х)=0,5.