43. Понятие «нелинейная корреляция».

В экономических приложениях часто возникает необходимость выражать корреляционную зависимость в виде нелинейных уравнений регрессии, поскольку линейные зависимости приводят к большим ошибкам. Выбор вида нелинейной регрессии называется спецификацией или этапом параметризации модели и осуществляется методами визуального оценивания точек корреляционного поля, анализа сути наблюдаемых экономических процессов и т.п. Наиболее часто в экономических исследованиях используют следующие виды нелинейной регрессии:

• Полиноминальная ;

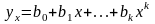• Гиперболическая ;

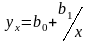• Степенное 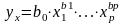и т.п.

Для определения неизвестных параметров выбранного уравнения регрессии используется метод наименьших квадратов.

При нелинейной регрессии для оценки тесноты связи между переменными используют не коэффициент корреляции , а индекс корреляции и коэффициент детерминации .

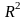Индекс корреляции по вычисляется по формул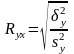е: , где 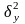- межгрупповая дисперсия, выражающая ту часть вариации переменной , которая обусловлена изменчивостью переменной или регрессией и вычисляемая по формуле: 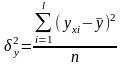; 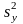- общая дисперсия переменной: .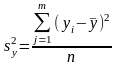

_{Коэффициент детерминации, равный квадрату индекса корреляции, показывает долю общей вариации зависимой переменной, обусловленной} регрессией или изменчивостью объясняющей переменной:

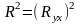
44. Анализ соответствия регрессионной модели наблюденным данным.

Для того, чтобы установить, соответствует ли выбранная регрессионная модель экспериментальным данным, используют основное уравнение дисперсионного анализа: 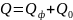, где – общая сумма квадратов отклонений У от средней, 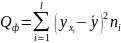– сумма квадратов, обусловленная регрессией, 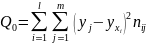– остаточная сумма квадратов.

Для несгруппированной выборки формулы несколько упрощаются: , , .

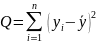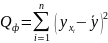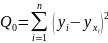Для заданного уровня α находим критическое значение Fкр распределения Фишера при k1=l-1, k2=n-l степенях свободы, где n – число наблюдений, l – число групп в корреляционной таблице или число оцениваемых параметров в несгруппированной выборке. Если статистика 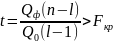, то уравнение регрессии считается значимым, т.е. соответствующим экспериментальным данным на уровне значимости α.

В случае линейной регрессии при l=2 уравнение регрессии значимо на уровне α, если .

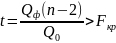Воздействие неучтенных случайных факторов в линейной модели определяется остаточной дисперсией σ0 в квадрате. Оценкой этой дисперсии является выборочная остаточная дисперсия .

регрессией или изменчивостью объясняющей

переменной:

.