
- •Случайные события и их классификация.
- •Классическое определение вероятности.
- •Аксиоматическое определение вероятности. Геометрическое определение вероятности.
- •Условная вероятность. Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Байеса.
- •Наивероятнейшее число наступлений события.
- •Локальная теорема Муавра – Лапласа
- •Интегральная теорема Лапласа.
- •Функция распределения случайной величины и ее свойства.
- •Дискретные случайные величины.
- •Плотность распределения вероятностей и ее свойства.
- •Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
- •Дисперсия случайной величины и ее свойства.
- •Биноминальный закон распределения. Математическое ожидание и дисперсия случайной, величины распределенной по биноминальному закону.
- •Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.
- •Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
- •Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
- •Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
- •Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
- •Корреляционный момент и коэффициент корреляции и их свойства.
- •Моменты случайной величины. Ассиметрия и эксцесс.
- •Неравенство Маркова и Чебышева.
- •Закон больших чисел « в форме» теоремы Чебышева.
- •Теорема Бернулли.
- •Понятие о «центральная предельная теорема». Теорема Ляпунова.
- •Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.
- •Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.
- •Выборочный метод. Точечное оценивание.
- •Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
- •Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
- •Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
- •Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.
- •Критерий Пирсона.
- •Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.
- •Критерий согласия Колмогорова.
- •Однофакторный дисперсионный анализ.
- •Модели и основные понятия корреляционного и регрессионного анализа.
- •Линейная корреляционная зависимость и прямые регрессии.
- •Коэффициент линейной корреляции и его свойства.
- •Понятие «нелинейная корреляция».
- •Анализ соответствия регрессионной модели наблюденным данным.
Линейная корреляционная зависимость и прямые регрессии.
Линейную
корреляционную зависимость между
переменными
и
выражают в виде линейного уравнения
регрессии:
 или
или
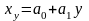 ,
неизвестные
параметры которых находим методом
наименьших квадратов.
,
неизвестные
параметры которых находим методом
наименьших квадратов.
Система нормальных уравнений для определения параметров линейной регрессии:
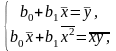
где соответствующие средние определяются по формулам:
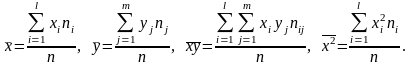
Подставляя
значения
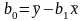 в уравнение регрессии
получаем:
в уравнение регрессии
получаем:
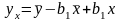 или
или
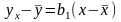 ,
где
коэффициент
,
где
коэффициент
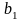 получил название коэффициента
регрессии
по
и обозначение
получил название коэффициента
регрессии
по
и обозначение
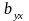 .
Этот коэффициент показывает на сколько
единиц в среднем изменяется переменная
при
увеличении переменной
на одну единицу.
.
Этот коэффициент показывает на сколько
единиц в среднем изменяется переменная
при
увеличении переменной
на одну единицу.
Решая систему
нормальных уравнений, найдем
:
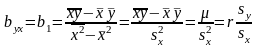 ,
где
,
где
 -
выборочная дисперсия переменной
:
-
выборочная дисперсия переменной
: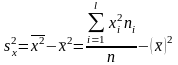 ,
-
выборочный корреляционный момент или
выборочная ковариация:
,
-
выборочный корреляционный момент или
выборочная ковариация:
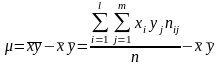 ,
-
выборочный коэффициент корреляции:
,
-
выборочный коэффициент корреляции:
 .
.
Уравнение регрессии
по
окончательно
выглядит следующим образом:
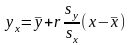 .
.
Рассуждая аналогично
находят уравнение регрессии
по
:
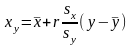 .
.
Сравнение уравнения регрессии, полученные методом наименьших квадратов, с уравнением регрессии двумерной случайной величины с нормальным законом распределения показывает их идентичность.
Коэффициент линейной корреляции и его свойства.
Для оценки тесноты связи между переменными и по выборочным значениям используют статистический коэффициент корреляции : .
Если данные не
сгруппированы в виде корреляционной
таблицы и представляют
пар чисел
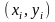 ,
то для вычисления коэффициента корреляции
проводят по следующей формуле:
,
то для вычисления коэффициента корреляции
проводят по следующей формуле:
 .
.
Между коэффициентом
корреляции
и
коэффициентами регрессии
и
 существует
связь:
существует
связь:
 ,
,
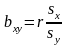 ,
,
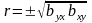 .
.
Основные свойства коэффициента корреляции (при достаточно большом объеме выборке ):
симметричен: rxy=ryx
-1≤rxy≤1
|rxy|=1, то связь между переменными – функциональная (уравнение линии).
При
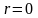 корреляционная линейная
связь отсутствует.
корреляционная линейная
связь отсутствует.
Для выяснения значимости коэффициента корреляции проверяется гипотеза об отсутствии линейной корреляционной связи между переменными Х и У, т.е. : р=0 (генеральный коэффициент корреляции). При справедливости этой гипотезы статистика (критерий) имеет - распределение Стьюдента с степенями свободы. При заданном уровне значимости и степени свободы находим по таблицам закона распределения Стьюдента критическое значение . Если , то нулевая гипотеза об отсутствии корреляционной связи между переменными и отвергается и переменные считаются зависимыми. При нет оснований отвергать нулевую гипотезу. Значимость коэффициента корреляции свидетельствует и о значимости коэффициентов регрессии, соответственно и о значимости линейного уравнения регрессии.
