
- •Случайные события и их классификация.
- •Классическое определение вероятности.
- •Аксиоматическое определение вероятности. Геометрическое определение вероятности.
- •Условная вероятность. Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Байеса.
- •Наивероятнейшее число наступлений события.
- •Локальная теорема Муавра – Лапласа
- •Интегральная теорема Лапласа.
- •Функция распределения случайной величины и ее свойства.
- •Дискретные случайные величины.
- •Плотность распределения вероятностей и ее свойства.
- •Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
- •Дисперсия случайной величины и ее свойства.
- •Биноминальный закон распределения. Математическое ожидание и дисперсия случайной, величины распределенной по биноминальному закону.
- •Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.
- •Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
- •Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
- •Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
- •Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
- •Корреляционный момент и коэффициент корреляции и их свойства.
- •Моменты случайной величины. Ассиметрия и эксцесс.
- •Неравенство Маркова и Чебышева.
- •Закон больших чисел « в форме» теоремы Чебышева.
- •Теорема Бернулли.
- •Понятие о «центральная предельная теорема». Теорема Ляпунова.
- •Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.
- •Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.
- •Выборочный метод. Точечное оценивание.
- •Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
- •Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
- •Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
- •Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.
- •Критерий Пирсона.
- •Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.
- •Критерий согласия Колмогорова.
- •Однофакторный дисперсионный анализ.
- •Модели и основные понятия корреляционного и регрессионного анализа.
- •Линейная корреляционная зависимость и прямые регрессии.
- •Коэффициент линейной корреляции и его свойства.
- •Понятие «нелинейная корреляция».
- •Анализ соответствия регрессионной модели наблюденным данным.
Однофакторный дисперсионный анализ.
Дисперсионный анализ – статистический метод оценки влияния различных факторов на результаты эксперимента.
Однофакторная
дисперсионная модель имеет вид: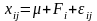 ,
где
,
где
 -значение
исследуемой переменной, полученной на
-значение
исследуемой переменной, полученной на
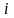 -м
уровне фактора (
-м
уровне фактора ( )
с
)
с
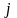 -м
порядковым номером (
-м
порядковым номером ( );
);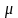 - общая средняя;
- общая средняя;
 -
эффект, обусловленный влиянием
-го
уровня фактора, т.е. вариация переменной
между отдельными уровнями фактора;
-
эффект, обусловленный влиянием
-го
уровня фактора, т.е. вариация переменной
между отдельными уровнями фактора;
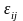 -случайная
компонента, или возмущение, вызванное
влиянием неконтролируемых факторов,
т.е. вариация переменной внутри отдельного
уровня фактора.
-случайная
компонента, или возмущение, вызванное
влиянием неконтролируемых факторов,
т.е. вариация переменной внутри отдельного
уровня фактора.
Рассмотрим сумму
квадратов отклонений
от общей средней
 в виде :
в виде :
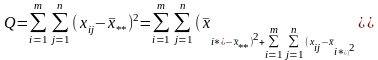
Или
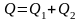 :
где
:
где
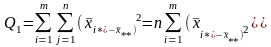 -
сумма квадратов отклонений групповых
средних от общей средней, или межгрупповая
(факторная)
сумма квадратов отклонений;
-
сумма квадратов отклонений групповых
средних от общей средней, или межгрупповая
(факторная)
сумма квадратов отклонений; -
сумма квадратов отклонений наблюдений
от групповых средних, или внутригрупповая
(остаточная) сумма квадратов отклонений.
-
сумма квадратов отклонений наблюдений
от групповых средних, или внутригрупповая
(остаточная) сумма квадратов отклонений.
В дисперсионном
анализе изменчивость показателя
оценивается не по суммам квадратов
отклонений, а по выборочным дисперсиям
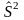 ,
которые являются несмещенными оценками
соответствующих дисперсий генеральных
совокупностей:
,
которые являются несмещенными оценками
соответствующих дисперсий генеральных
совокупностей:
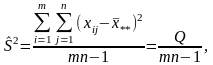
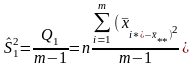
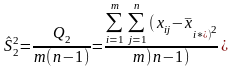 ,
,
где
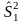 и
и
 -
получили название межгрупповой и
внутригрупповой дисперсиями.
-
получили название межгрупповой и
внутригрупповой дисперсиями.
Межгрупповая и
внутригрупповая дисперсии являются
несмещенными оценками общей дисперсии
генеральной совокупности и проверка
нулевой гипотезы
сводится к проверки
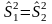 .
Для этого вычисляется критерий
(статистика):
.
Для этого вычисляется критерий
(статистика):
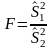 .
.
При правильности
нулевой гипотезы
критерий
должен
подчиняться закону распределения
Фишера со степенями свободы
 и
и
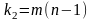 .
Поэтому при заданном уровне значимости
критическое значение
.
Поэтому при заданном уровне значимости
критическое значение
 критерия
находим по таблицам
критерия
находим по таблицам
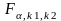 закона распределения Фишера.
закона распределения Фишера.
Если
 ,
то нулевая гипотеза отвергается и
делается заключение о существенности
влияния фактора
на случайную величину.
,
то нулевая гипотеза отвергается и
делается заключение о существенности
влияния фактора
на случайную величину.
При
 нет оснований отвергать гипотезу
и считают, что влияние фактора
несущественно.
нет оснований отвергать гипотезу
и считают, что влияние фактора
несущественно.
Модели и основные понятия корреляционного и регрессионного анализа.
Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Простейшая
корреляционная зависимость может быть
представлена в виде уравнения регрессии: или
или
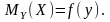 А их графики – линии регрессии. Такое
представление зависимости между
переменной Х и У называется полем
корреляции.
А их графики – линии регрессии. Такое
представление зависимости между
переменной Х и У называется полем
корреляции.
Выборочный
коэффициент корреляции характеризует
тесноту связи между случайными
переменными
и
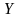 в генеральной совокупности:
в генеральной совокупности:
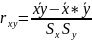 , где Sx,
Sy
– выборочные оценки стандартного
квадратического отклонения генеральной
совокупности.
, где Sx,
Sy
– выборочные оценки стандартного
квадратического отклонения генеральной
совокупности.
Для выяснения
значимости коэффициента корреляции
проверяется гипотеза
об отсутствии линейной корреляционной
связи между переменными Х и У, т.е.
:
р=0 (генеральный коэффициент корреляции).
При справедливости этой гипотезы
статистика (критерий)
 имеет
- распределение Стьюдента с
имеет
- распределение Стьюдента с
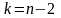 степенями свободы. При заданном уровне
значимости
и степени свободы
степенями свободы. При заданном уровне
значимости
и степени свободы
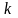 находим по таблицам закона распределения
Стьюдента критическое значение
находим по таблицам закона распределения
Стьюдента критическое значение
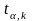 .
Если
.
Если
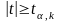 ,
то нулевая гипотеза об отсутствии
корреляционной связи между переменными
и
отвергается
и переменные считаются зависимыми. При
,
то нулевая гипотеза об отсутствии
корреляционной связи между переменными
и
отвергается
и переменные считаются зависимыми. При
 нет оснований отвергать нулевую
гипотезу. Значимость коэффициента
корреляции свидетельствует и о значимости
коэффициентов регрессии, соответственно
и о значимости линейного уравнения
регрессии.
нет оснований отвергать нулевую
гипотезу. Значимость коэффициента
корреляции свидетельствует и о значимости
коэффициентов регрессии, соответственно
и о значимости линейного уравнения
регрессии.
Основной метод нахождения неизвестных параметров уравнений регрессии в статистических исследованиях является метод наименьших квадратов.
Корреляционная матрица представляет собой симметичную матрицу размером m*m – число переменных:
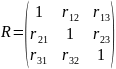
По правила построения корреляционной матицы: r12=r21, r13=r31, r23=r32.
