
- •Случайные события и их классификация.
- •Классическое определение вероятности.
- •Аксиоматическое определение вероятности. Геометрическое определение вероятности.
- •Условная вероятность. Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Байеса.
- •Наивероятнейшее число наступлений события.
- •Локальная теорема Муавра – Лапласа
- •Интегральная теорема Лапласа.
- •Функция распределения случайной величины и ее свойства.
- •Дискретные случайные величины.
- •Плотность распределения вероятностей и ее свойства.
- •Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
- •Дисперсия случайной величины и ее свойства.
- •Биноминальный закон распределения. Математическое ожидание и дисперсия случайной, величины распределенной по биноминальному закону.
- •Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.
- •Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
- •Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
- •Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
- •Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
- •Корреляционный момент и коэффициент корреляции и их свойства.
- •Моменты случайной величины. Ассиметрия и эксцесс.
- •Неравенство Маркова и Чебышева.
- •Закон больших чисел « в форме» теоремы Чебышева.
- •Теорема Бернулли.
- •Понятие о «центральная предельная теорема». Теорема Ляпунова.
- •Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.
- •Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.
- •Выборочный метод. Точечное оценивание.
- •Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
- •Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
- •Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
- •Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.
- •Критерий Пирсона.
- •Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.
- •Критерий согласия Колмогорова.
- •Однофакторный дисперсионный анализ.
- •Модели и основные понятия корреляционного и регрессионного анализа.
- •Линейная корреляционная зависимость и прямые регрессии.
- •Коэффициент линейной корреляции и его свойства.
- •Понятие «нелинейная корреляция».
- •Анализ соответствия регрессионной модели наблюденным данным.
Случайные события и их классификация.
Пространством элементарных событий называют множество взаимоисключающих исходов эксперимента такое, что каждый интересующий результат эксперимента может быть однозначно описан с помощью элементов этого множества. Элементы называются элементарными событиями и обозначаются .
Событием называют любое подмножество элементов из . Событие произойдет, если произойдет какое-либо из элементарных событий . Пустое множество называется невозможным событием.
Суммой двух событий и называется событие + , состоящее из элементарных событий, принадлежащих хотя бы одному из событий или .
Произведением двух событий и называется событие , состоящих из элементарных событий, принадлежащих одновременно и .
Противоположным событием событию называют событие , состоящее из элементарных событий, не принадлежащих .
Разностью двух событий и называют событие \, состоящее из элементарных событий, которые входят в событие .
События и называются несовместными , если у них нет общих элементарных событий.
Пусть F - поле событий для данного эксперимента. Вероятностью P(A) называется числовая функция, определенная на всех F и удовлетворяющая трем условиям (аксиомам вероятностей):
P(A) 0;
P()=1;
Для любой конечной или бесконечной последовательности наблюдаемых событий
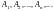 таких,
что
таких,
что
 при
при
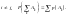
Классическое определение вероятности.
При данном способе пространство элементарных событий является конечным, и все элементарные события равновероятны. Тогда вероятность события определяется равенством
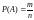 ,
где
,
где
 -
число элементарных исходов испытания,
благоприятствующих
появлению
события
-
число элементарных исходов испытания,
благоприятствующих
появлению
события ;
;
 -
общее число возможных элементарных
исходов испытания.
-
общее число возможных элементарных
исходов испытания.
Статистическое определение вероятности.
При данном способе
рассматривается случайный эксперимент
для которого построить пространство
элементарных событий невозможно. Тогда
эксперимент проводится
 раз при неизменном комплексе условий
протекания и подсчитывается число
экспериментов, в которых появилось
некоторое событие
раз при неизменном комплексе условий
протекания и подсчитывается число
экспериментов, в которых появилось
некоторое событие
 .
Тогда вероятность вычисляется по
формуле
.
Тогда вероятность вычисляется по
формуле
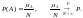
На практике, при
вычислениях вероятностей в классической
схеме часто приходиться пользоваться
формулами комбинаторики
(соединений).
Каждая из комбинаторных формул
определяет общее число элементарных
событий в некотором эксперименте,
состоящем в выборе наудачу
 элементов из
элементов из
 различных элементов исходного множества.
Существуют две принципиально различные
схемы выбора:
различных элементов исходного множества.
Существуют две принципиально различные
схемы выбора:
а) без возращения элементов;
б) с возвращением.
1. Перестановки.
Возьмем
 различных элементов
различных элементов
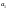 ,
, будем
переставлять эти элементы всевозможными
способами, оставляя неизменным их число
и меняя лишь их порядок. Каждая из
полученных таким образом комбинаций
носит название перестановки.
Общее число перестановок из
будем
переставлять эти элементы всевозможными
способами, оставляя неизменным их число
и меняя лишь их порядок. Каждая из
полученных таким образом комбинаций
носит название перестановки.
Общее число перестановок из
 элементов обозначается
элементов обозначается
 и равно
и равно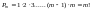

2. Размещения.
Будем составлять из
 различных элементов множества по
элементов
в каждом, отличающихся либо набором
элементов, либо порядком их следования.
Полученные при этом комбинации элементов
называются размещениями
из
различных элементов множества по
элементов
в каждом, отличающихся либо набором
элементов, либо порядком их следования.
Полученные при этом комбинации элементов
называются размещениями
из
 элементов по
элементов по
 и обозначается
и обозначается
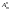 .
Их общее число равно:
.
Их общее число равно: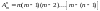 .
.
3.
Сочетания.
Из
различных элементов будем составлять
множества по
элементов,
имеющих различный состав. Полученная
при этом комбинации элементов называются
сочетаниями
из
элементов по
.
Общее число различных между собой
сочетаний обозначается
 и вычисляется по следующим формулам:
и вычисляется по следующим формулам:
 или
или .
.
