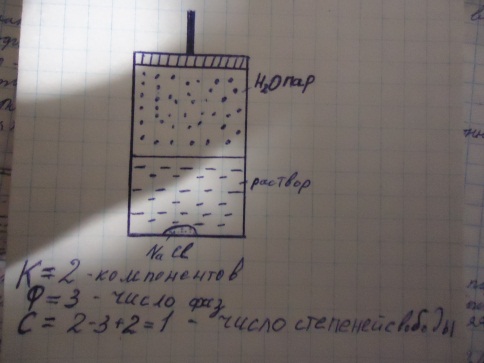
19) Закон равновесия фаз.

Правило фаз Гиббса.

Рассмотрим систему, состоящую из К компонентов и Ф фаз.

Для описания состояния этой системы нужно задать температуру, давление, концентрацию каждого компонента в каждой фазе. В равновесии температура и давление в каждой фазе одинаковы.

Для задания состава одной фазы нужно задать (К-1) концентрацию, а для задания состава всех фаз (К-1)Ф концентраций.

Всего (К-1)Ф+2 параметра

Не все параметры в равновесии являются независимыми.

В равновесии:

- количество уравнений

Обозначим С – число независимых параметров (число степеней свободы).

Числом степеней свободы называется число параметров, которые можно произвольно изменять в некоторых пределах, не изменяя при этом числа и вида фаз.

Формулировка правила фаз Гиббса.

С=К-Ф+2

Число степеней свободы равновесной термодинамической системы, на которую из внешних параметров могут влиять только температура и давление, равно числу независимых компонентов, минус число фаз, плюс два.

Если на систему влияют другие параметры, кроме давления и температуры (сила тяжести, напряженность электрического поля), то в общем случае

С=К-Ф+N,

где N – число внешних параметров.

Наоборот, если один из параметров: давление или температура не влияют на состояние системы, то условное число степеней свободы

Из правила фаз Гиббса следует

так как

Различают системы:

1-однофазные, двухфазные и тд.

2-однокомпонентные, двухкомпонентные и т.д.

3-инвариантные или безвариантные (С=0);

моновариантные или одновариантные (С=1);

дивариантные или двухвариантные (С=2);

Пример насыщенный раствор NaCl+HOH. Это значит, что только один из трех параметров(давление, концентрация и температура) можно произвольно изменять в некоторых пределах не изменяя при этом числа или вида фаз. Например если повысить температуру, то р и концентрация NaCl увеличатся. Если менять 1 параметр, то остальные параметры меняются вынужденно. Если попытаться увеличить давление опуская вниз поршень уменьшая объем поддерживая Т-const, то давление изменятся не будет, а будет происходить конденсация пара.

21) Однокомпонентные системы. Уравнение Клапейрона – Клаузиуса.

Рассмотрим однокомпонентную систему, состоящую из двух фаз.

Химический потенциал компонента в однокомпонентной системе равняется молярной энергии Гиббса.

В равновесии

Если изменить давление и температуру, то молярная энергия Гиббса изменится. Если при этом фазовые равновесия не нарушаются, то

Используя зависимость энергии Гиббса от давления и температуры,

получим

= ,

где - молярный объем и энтропия вещества в 1 и во 2 фазе.

где - изменение молярного объема и энтропии при переходе вещества из 1 во 2 фазу.

Так как обе фазы находятся при одинаковой температуре, то фазовый переход является изотермическим.

уравнение Клапейрона-Клаузиуса.

Оно справедливо для любых двух фаз и выражает связь давления и температуры при фазовом равновесии.

Анализ уравнения.

Пример: кристаллизация воды

ж→тв

температура увеличивается, давление уменьшается, если сохраняется фазовое равновесие.

тв→ж

давление увеличивается, температура плавления льда понижается.

График зависимости температуры плавления от давления.

Для большинства веществ ∆V при плавлении > 0, поэтому с ростом давления температура плавления увеличивается.

Если одна из двух фаз газообразная, то

Пример: нормальные условия р=1атм, t=0^oC, n=1моль, V_газа=22,4литра, V_{жидкое HOH}=18мл=0,018л. ж→газ ∆V=22,4-0,018=22,4л

Используя уравнение состояния идеального газа (для 1 моля).

Подставим в уравнение Клапейрона-Клаузиуса.

уравнение Клапейрона-Клаузиуса.

Это уравнение справедливо для равновесия двух фаз, одна из которых газообразная.

Анализ уравнения.

При переходе ж→пар

Температура увеличивается, давление насыщенного пара увеличивается.

Интегрируя уравнение Клаперона-Клаузиуса, получим

если

уравнение кривой пара.

Измеряя давление насыщенного пара над жидкостью, можно определить теплоту испарения жидкости.

Аналитический метод.

1.

2.

В не очень большом интервале можно принять постоянным.

Графический метод.

Берем неопределенный интеграл

уравнение прямой y=Ax+B