16) Тепловая теорема Нернста.
Уравнение Гиббса- Гельмгольца позволяет рассчитать энергию Гиббса реакции ∆G при любой температуре Т. Однако при интегрировании этого уравнения появляются постоянные. Эти постоянные можно определить из опыта, однако в этом случае теория оказывается не полной. Теорема Нернста позволяет рассчитать энергию Гиббса ∆G без экспериментальных данных, использую теплоемкости веществ. Теорема: экспериментально установлено, что при понижении температуры разница между ∆G и ∆H уменьшается.
Постулат Нернста:
В
конденсированных системах, вблизи
абсолютного нуля температур, ∆G
и ∆Н совпадают (1 ), имеют общую касательную
(2), параллельную оси температур (3 ).
Постулат Планка. 3-й закон термодинамики.
При понижении температуры энтропия уменьшается:
Постулат: При абсолютном нуле температур энтропия правильно образованного кристалла любого вещества в чистом виде равна нулю.
.
В любом другом состоянии энтропия > 0 (для смеси веществ, для кристаллов с дефектами при температуре не равной нулю) в статической термодинамике. Следствие: постулат Планка позволяет вычислить абсолютное значение энтропии
при р= const
17) Расчет константы равновесия с помощью абсолютных значений энтропии.
Тепловой эффект реакции при заданной температуре можно найти с помощью Кирхгоффа
,
а при стандартной температуре- с помощью уравнения Гесса
где
=
Окончательно получим
18) Фазовые равновесия.
Фазовые равновесия – это равновесия в гетерогенных системах, в которых не протекают химические реакции.
Примеры: равновесие жидкость-пар, кристаллы-жидкость, кристаллы-пар.
Основные определения:
Фаза – это совокупность гомогенных частей системы, одинаковых по составу, химическим и физическим свойствам и отделенных от других частей поверхностью раздела.
Компонент (составная часть) – это вещество, которое может быть выделено из системы, и существовать отдельно.
Число независимых компонентов – это наименьшее число компонентов, через которые можно выразить состав любой фазы.
Пример: в газовой фазе 2NO+O2=2NO2, Pобщ=1 атм. Всего компонентов 3, независимых компонентов 2. В равновесии К=Р2 NO2 /P2NO+PO2.
Условие фазового равновесия компонента в различных фазах.
Рассмотрим систему, состоящую из двух фаз α и β, каждая из которых состоит из одного или нескольких компонентов.
-
химический потенциал ί компонента в
фазе α.
Общая энергия Гиббса всей системы
Пусть
некоторое количество i-го
компонента
переходит из фазы α в фазу β, тогда
изменение энергии Гиббса в фазе α. и в
фазе β:
Изменение общей энергии Гиббса
Если компонент не переходит из фазы α в β, а находится в этих фазах в равновесии, то из общего термодинамического условия равновесия
получим
-
условие фазового равновесия
Компонент находится в равновесии в фазах α и β, если его химический потенциал в этих фазах одинаков.
Если химический потенциал компонентов не одинаков, то компонент переходит из одной фазы в другую.
Из общего термодинамического условия самопроизвольного процесса
Компонент самопроизвольно переходит из фазы с большим химическим потенциалом этого компонента в фазу с меньшим химическим потенциалом.
Пример: μi= μi+RTlnPi, NaCl в HOH μ1 HOH> μ2 HOH.
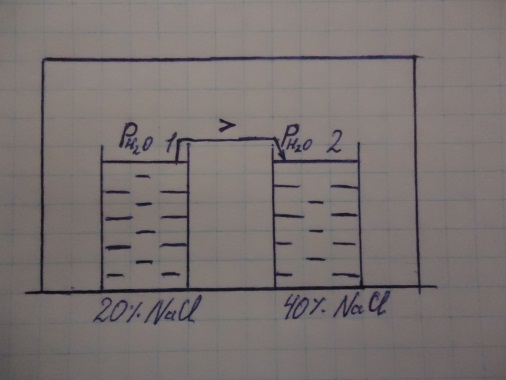
Химический потенциал.
Для однокомпонентной системы зависимость энергии Гиббса от температуры и давления выражается уравнением
.
Для многокомпонентной системы энергия Гиббса зависит не только от температуры и давления, но и от количества каждого компонента
.
При p и T= const
Обозначим
-
химический потенциал компонента – это
частная производная общей энергии
Гиббса системы по количеству данного
компонента [Дж/моль]. Химический
потенциал имеет смысл энергии Гиббса,
приходящейся на 1 моль данного компонента,
находящегося в смеси с другими
компонентами. Зависимость химического
потенциала от давления такая же, как
и у молярной энергии Гиббса однокомпонентной
системы для идеального газа
Для неидеального газа нужно заменить на фугитивность f .
-
относительное давление. Пример:
º=
760 мм .рт .ст .,
= 380 мм. рт. ст. , значит
=
0.5 ;
º
=1 атм.,
=0.5 атм., значит
=
0,5. Тогда химический потенциал
