5) Зависимость теплового эффекта от температуры

Найдем произвольную теплового эффекта по температуре.

1. При постоянном давлении (p=const).

- уравнение Кирхгофа.

2. При постоянном объеме (V=const).

- уравнение Кирхгофа.

- называется температурный коэффициент теплового эффекта процесса

Закон: температурный коэффициент теплового эффекта процесса равен изменению теплоемкости в ходе процесса.

6) Второе начало термодинамики.

Первый закон термодинамики позволяет определить, какое количество энергии можно получить в результате того или иного процесса, однако он не определяет возможность самопроизвольного протекания процесса.

Пример: Первый закон термодинамики не запрещает переход теплоты от холодного тела к горячему, т.к. общий запас энергии при этом сохраняется. Следовательно, в природе существует еще один закон, который определяет направление самопроизвольного протекания процесса.

Примеры самопроизвольных процессов.

1. Переход теплоты от горячего тела к холодному до выравнивания температур.

2. Диффузия, протекающая до выравнивания концентрации.

3. Превращение энергии упорядоченного движения в энергию беспорядочного движения при трении и неупругом ударе.

Как показывает опыт, самопроизвольное обратное протекание этих процессов не возможно, оно возможно лишь при воздействии внешних устройств, поэтому самопроизвольно протекающие процессы необратимы.

Формулировки второго закона термодинамики.

1. Клаузиус.

Никакая совокупность процессов не может сводиться к передачи теплоты от холодного тела к теплому.

2. Томсон.

Никакая совокупность процессов не может сводиться к превращению теплоты в работу.

Пример: изотермический процесс с идеальным газом.

T=const

U=const

В этом процесс вся полученная теплота превращается в работу, но это не единственный результат процесса, другой результат – расширение газа.

3) Оствальд.

Вечный двигатель второго рода невозможен.

Вечным двигателем второго рода называется периодически действующие устройство, в котором вся теплота превращается в работу.

Схема работающего теплового двигателя.

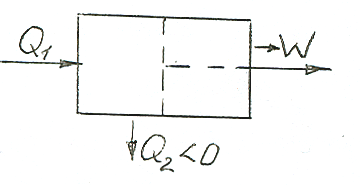
(Статистическая термодинамика) на основе представления о молекулярном строении тел.

Процессы самопроизвольно протекают в сторону наиболее вероятного состояния, наиболее вероятным является такое макросостояние, которое может осуществляться наибольшим количеством микросостояний. Наиболее вероятным является состояние наибольшего беспорядка, поэтому все самопроизвольные процессы в изолированной системе протекают в сторону наибольшего беспорядка, следовательно, в сторону выравнивания неоднородностей (температуры, давления и т.д.) и превращения энергии упорядоченного движения в энергию беспорядочного движения.

7) Математическая формулировка второго закона термодинамики

Необратимые процессы самопроизвольно протекают в направлении выравнивания неоднородностей и превращения энергии упорядоченного движения в энергию беспорядочного, эти процессы протекают до установления состояния равновесия.

Для того чтобы математически выразить этот закон, нужно найти функцию, значение которой в каждом состоянии показывало бы как далеко это состояние от равновесного, а изменение этой функции в ходе процесса показывало бы, приближается ли система к равновесию или удаляется от него.

Доказывается, что функция не зависит от пути процесса.

Т.о. эта функция является функцией состояния, ее называют энтропией.

- приведенная теплота.

Энтропией называется функция состояния, изменения которой равно сумме приведенных теплот в обратимом процессе.

В термодинамики доказывается так же, что по необратимому пути меньше, чем по обратимому.

- математическая формулировка.

Вычисление энтропии в некоторых термодинамических процессах.

1.Изотермический фазовый переход.T=const

тв. ж. п. , .

2.Изобарный процесс нагревания систем.p=const

, , , , .

=const

Вывод: , .При повышении температуры, энтропия возрастает.

3.Изохорный процесс нагревания системы. V=const

, , = ,

=const

4.Изотермическое расширение газов. T=const

=

U=const, , , ,

1 моль:

, , , .

При V₂>V_{1, .}

При расширении газа энтропия увеличивается.

Определение направления самопроизвольно протекающих процессов в изолированной системе.

В изолированной системе

В изолированной системе могут протекать только такие процессы, в ходе которых энтропия увеличивается.

Самопроизвольно процессы протекают до установления состояния равновесия при котором энтропия достигает максимального для данных условий значения.

Для неизолированной системы существуют другие критерии определения направления процесса.

Определение направления самопроизвольного протекания изохорно-изотермических процессов.

Введем функцию состояния A=U-TS, назовем ее энергией Гельмгольца или изохорно-изотермическим потенциалом.

Найдем ее изменение при изменении объема и температуры.

Из первого и из второго законов термодинамики:

Ограничимся рассмотрением работы расширения.

Уравнение выражает зависимость энергии Гельмгольца от температуры и объема.

При V,T=const.

При V,T=const процессы самопроизвольно протекают в направлении уменьшения энергии Гельмгольца.

Процессы протекают до установления равновесия, при котором .