Азеотропные смеси

При значительных отклонениях от свойств идеальных растворов на кривых давление – состав и температура – состав появляются точки экстреммума.

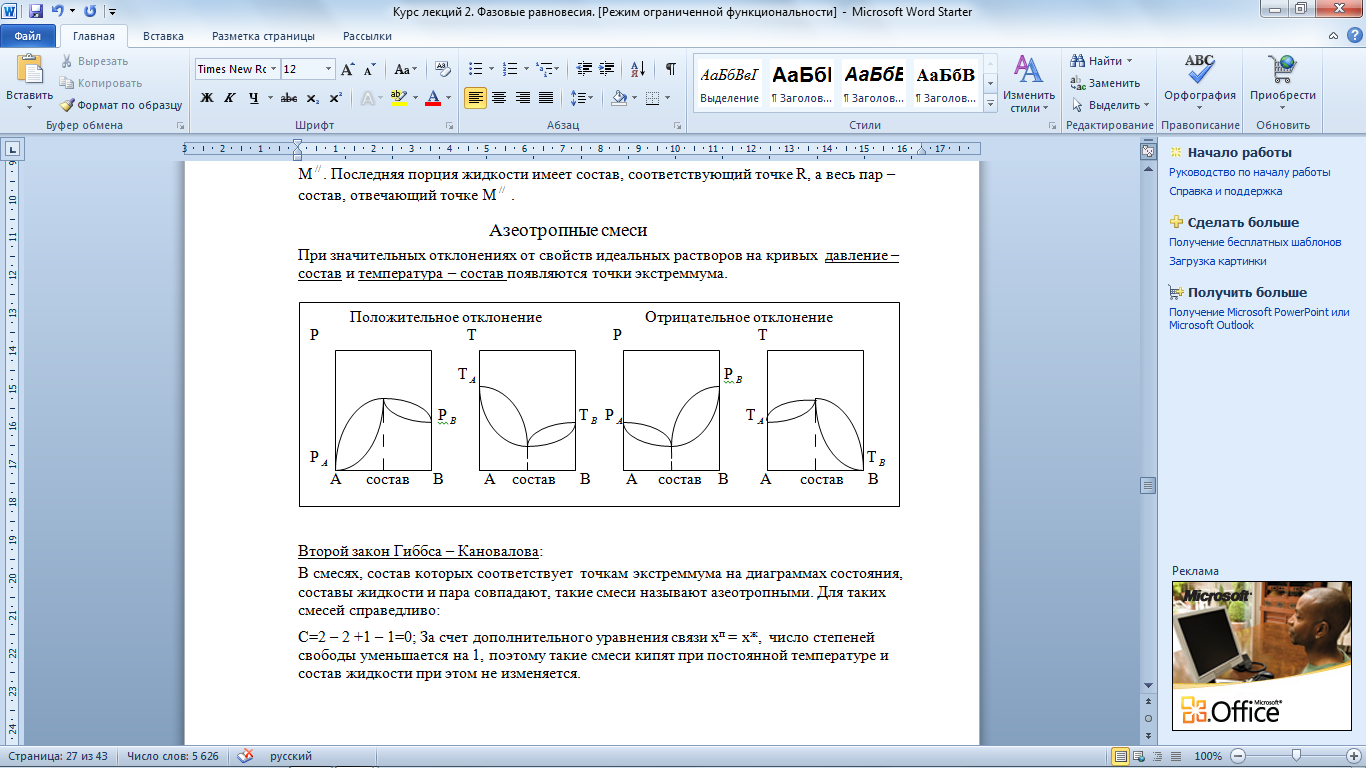
Второй закон Гиббса – Кановалова:

В смесях, состав которых соответствует точкам экстреммума на диаграммах состояния, составы жидкости и пара совпадают, такие смеси называют азеотропными. Для таких смесей справедливо:

С=2 – 2 +1 – 1=0; За счет дополнительного уравнения связи x^п = x^ж, число степеней свободы уменьшается на 1, поэтому такие смеси кипят при постоянной температуре и состав жидкости при этом не изменяется.

27) Диаграммы равновесия пар – жидкий раствор

Для описания состояния двухкомпонентной системы нужно задать три параметра: температуру, давление, концентрацию. Графически изобразить состояние системы можно точкой на трехмерной диаграмме, эта точка называется фигуративной. Для того чтобы изобразить состояние системы на плоской диаграмме нужно зафиксировать одну из переменных. Обычно применяют два вида диаграмм:1)- давление пара – состав (T=const); 2)- Т_кип – состав (Р=const).

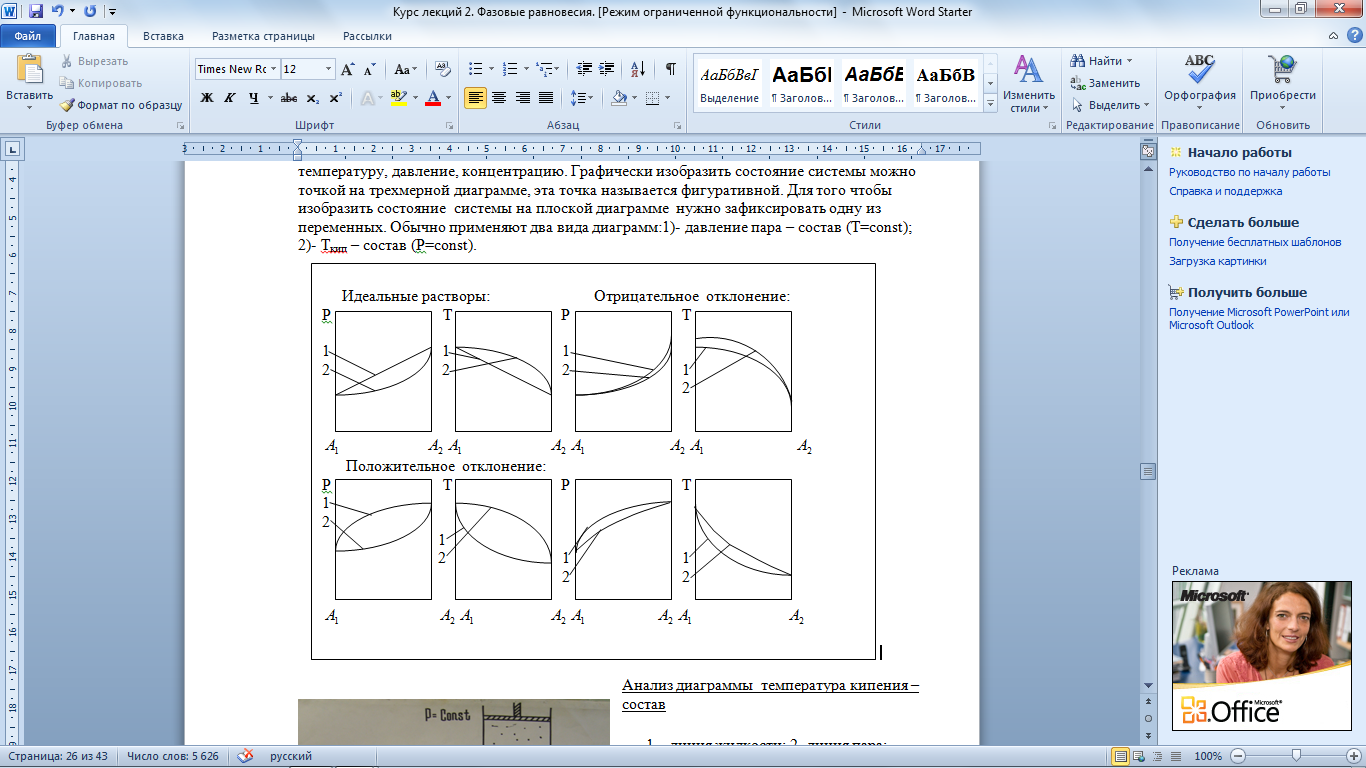
Анализ диаграммы температура кипения – состав

1-линия жидкости; 2- линия пара;

С = К–Ф +2 – число степеней свободы ; С =К – Ф +1, при Р= const; К=2, С =3 – Ф;

Область ниже линии жидкости называют областью жидкой фазы. Ф=1, С =2;

Можно одновременно и произвольно изменять и температуру и состав в некоторых пределах при этом система остается однофазной. Область выше линии пара – область пара. Ф=1, С =2;

Область между линиями жидкости и пара – область равновесия пара и жидкого раствора. Ф=2, С =1; Можно произвольно изменять температуру при этом состав фаз будет изменяться.

Чтобы определить состав равновесных фаз в любой точке гетерогенной области, нужно через эту точку провести изотерму до пересечения с кривыми , ограничивающими эту область. Например:в точке М состав жидкости соответствует точке С(40 мольных % А + 60 мольных % А ). Состав пара соответствует точке Д(90% А + 10% А ).Относительное количество равновесных фаз определяется по правилу рычага: или ;

Рассмотрам процессы протекающие при повышении температуры жидкости с составом , отвечающим точке М. В точке Р начинается кипение. Первая порция пара имеет состав соответствующий точке Q (95%A +5%A ), пар обогащен компонентом А . При дальнейшем повышении температуры состав жидкости меняется – жидкость обогащается низколетучим компонентом А . Меняется и состав пара. Заканчивается кипение в точке М . Последняя порция жидкости имеет состав, соответствующий точке R, а весь пар – состав, отвечающий точке М .

28) Диаграммы равновесия кристаллы – жидкий расплав.

Состояние двухкомпонентной системы описывается тремя параметрами: Р,Т,С. Для того чтобы графически изобразить состояние системы на плоской диаграмме нужно зафиксировать один из параметров. Рассмотрим зависимости температуры кипения от состава при постоянном давлении (диаграммы плавкости). Условное число степеней свободы С_усл=К-Ф+1, т.к. Р=const, К=2.

Системы с неограниченной растворимостью компонентов в жидком состоянии и полной взаимной нерастворимостью в твердом состоянии.

Например: система сурьма – свинец: в жидком состоянии – раствор, а в твердом состоянии смесь кристаллов сурьмы с кристаллами свинца.

Диаграмма с простой эвтетикой:

О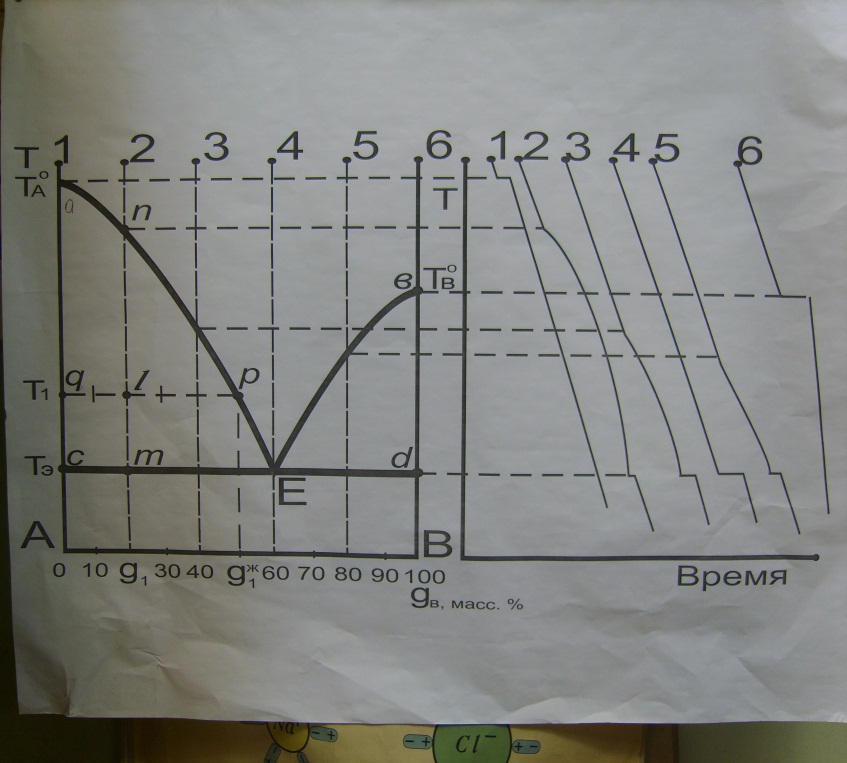 писание диаграммы:

Точки а и в изображают температуру кристализации чистых компонентов.

Линия аЕв – линия ликвидуса, выше нее система находится в жидком состоянии.

Линия сЕd – линия солидуса, ниже нее система находится в твердом состоянии.

Между линиями ликвидуса и солидуса система состоит из двух фаз: жидкой и твердой.

Для определения состава равновесных фаз в любой точке гетерогенной области нужно через эту точку провести изотерму до пересечения с кривыми, ограничивающими эту область.

Например: система с общим составом g₁ при температуре Т₁ (точка l) состоит из двух фаз кристаллов А (точка q) и жидкости с составом g₁ (точка Р).

Относительные массы твердой и жидкой фазы можно определить по правилу рычага:

; .

Точка Е – точка эвтектики (легкоплавящийся), она соответствует составу, имеющему наименьшую температуру начала кристаллизации расплава. При кристаллизации расплава с эвтектическим составом образуется мелкокристаллическая смесь, состоящая из кристаллов А и кристаллов В в таком же массовом соотношении, как и в жидкости. Эта смесь называется эвтектикой.

Диаграммы плавкости получают методом термического анализа. Метод заключается в получении кривых охлаждения, т.е. зависимость температуры системы от времени при охлаждении. По особым точкам на этих кривых строят диаграммы плавкости.

Анализ диаграммы.

Точка 1 – изображает чистое вещество А в жидком состоянии, число степеней свободы в точке 1: С_усл=К-Ф+1==1–1+1=1. Температура может понижаться.

В точке а – начинается кристаллизация вещества А, число степеней свободы С_усл=1–2+1=0. Температура понижатся не может до тех пор пока вся жидкость не закристаллизуется. На кривой охлаждения наблюдается температурная остановка, по окончании кристаллизации остается одна фаза С_усл=1–1+1=1. Температура может понижаться.

Точка 2 – изображает жидкий расплав с составом g₁: С=2–1+1=2. Можно изменять температуру и состав; температура может понижаться до точки n, в точке n – начинается кристаллизация, выпадают кристаллы А: С_усл=2–2+1=1. Температура может понижаться; причина понижения температуры в ходе кристаллизации: при выпадении из жидкости кристаллов А жидкоть обогащается компонентом В, ее состав меняется, меняется и температура кристаллизации.

На кривой охлаждения наблюдается излом. Скорость понижения температуры уменьшается. Это объясняется выделением теплоты при кристаллизации и как следствие уменшением скорости охлаждения.

В точке m начинается кристаллизация компонента В и продолжается кристаллизация компонента А. Состав жидкости соответствует точке Е и не изменяется. С=2–3+1=0. Температура понижаться не может. На кривой охлаждения температурная остановка, по окончании кристаллизации, остатся две фазы, появляется одна степень свободы: С=2–2+1=1. Температура может понижаться.

Точка 3 – аналогична точке 2, но кристаллизация начинается при меньшей температуре. На кривой охлаждения при эвтектической температуре температурная остановка длиннее, т.к. масса эвтектического расплава больше.

Точка 4 – соответствует расплаву эвтектического состава. В точке Е начинается кристаллизация, выпадают кристаллы А и В: С=2–3+1=0; на кривой охлаждения температурная остановка – ее длина наибольшая.

Точка 5 – при кристализации будут выпадать сначала кристаллы В, а при эвтектической температуре начнут выпадать кристаллы А.

Точка 6 – соответствует компоненту В в жидком состоянии. Кристаллизация происходит в точке в, на кривой охлаждения –