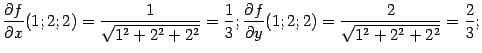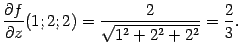- •Раздел 3. Дифференциальное исчисление.
- •Понятие функции. Способы задания. Графики функции в декартовой системе координат.
- •1.Табличный способ.
- •2.Графический способ.
- •2.Параметрическое задание функции. Циклоида. Вывод параметрического уравнения циклоиды.
- •1.11. Параметрическое задание функции
- •3.Понятие приращения функции , монотонность функции. Понятие функции ограниченной, четной, нечетной, периодической.
- •4. Понятие сложной функции. Понятие обратной функции.
- •1. Понятие о сложной функции
- •5.Основные элементарные функции и их графики. (представить конспект)
- •6. Понятие бесконечно малых функций , свойства бесконечно малых функций. Ответ:
- •7. Понятие предела функции. Основные теоремы о пределах.
- •8.Непрерывность функции в точке и на интервале. Свойства непрерывных функций.
- •9.Первый замечательный предел.
- •10. Понятие предела функции на бесконечности.
- •11.Второй замечательный предел
- •12.Нахождение асимптот к графику функции.
- •13. Понятие производной функции, ее механический и геометрический смысл. Понятие дифференцируемости функции в точке.
- •14. Связь между дифференцируемости и непрерывности функции.
- •15. Понятие дифференциала функции . Приближенные вычисления с помощью дифференциала.
14. Связь между дифференцируемости и непрерывности функции.
Ответ:
Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке. Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции. Обратное утверждение не верно.
Например, функция y=∣x∣ непрерывна в точке x=0, но не дифференцируема в этой точке. Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.
15. Понятие дифференциала функции . Приближенные вычисления с помощью дифференциала.
Ответ:
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
![]()
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать у/ х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким
образом, приращение функции ∆у
представляет собой сумму двух слагаемых
ƒ'(х)•∆х и а•∆х, являющихся бесконечно
малыми при ∆x→0. При этом первое слагаемое
есть бесконечно малая функция одного
порядка с ∆х, так как![]() а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
![]()
Поэтому первое слагаемое ƒ'(х) ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (1)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (1) можно записать так:
dy=ƒ'(х)dх, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.
Приближенные вычисления с помощью дифференциала функции.
Пример:
Пример 7.23 Пусть требуется приближённо вычислить значение
![]()
Рассмотрим функцию
![]()
и
будем трактовать числа ![]() как
малые отклонения на
как
малые отклонения на ![]() ,
, ![]() ,
, ![]() от
"круглых" значений
от
"круглых" значений ![]() .
.
Поскольку
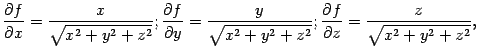
то дифференциал функции равен
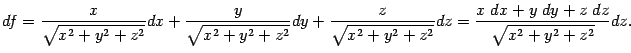
Значение
функции в точке ![]() равно
равно ![]() значения
частных производных равны
значения
частных производных равны
|
|
|
|
Поэтому
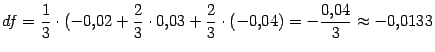
и
![]()
16. Производная сложной функции. Производная обратной функции.
Ответ:
Сложная функция.



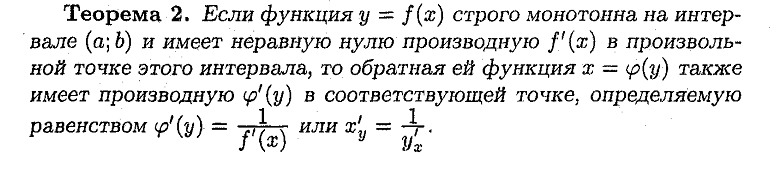
Обратная функция.


Примеры:

ых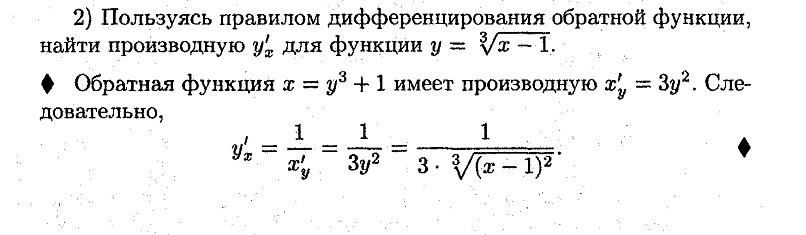
17. Вывод табличных производных.
Ответ:
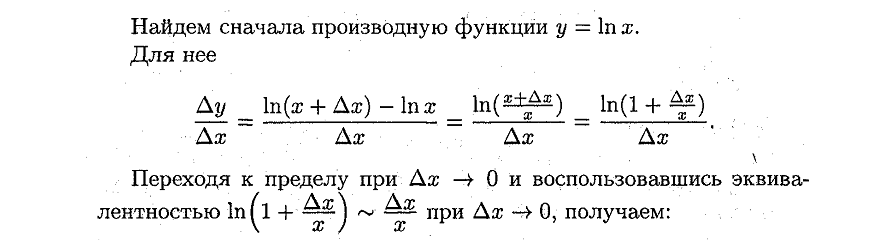
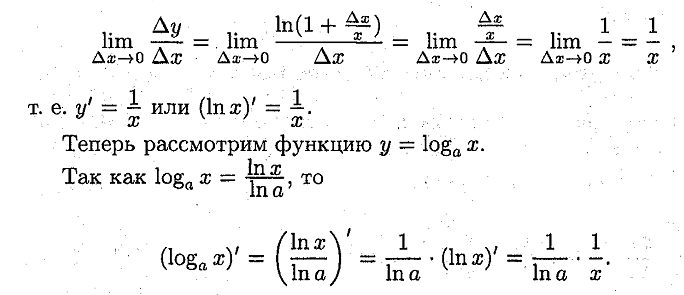
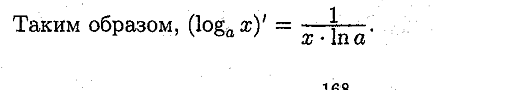
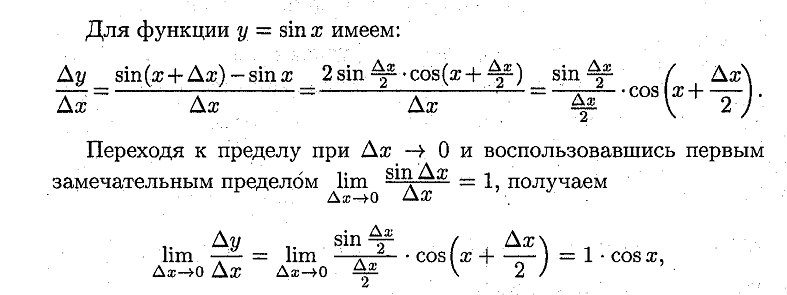
![]()
Нахождение производной для tgx
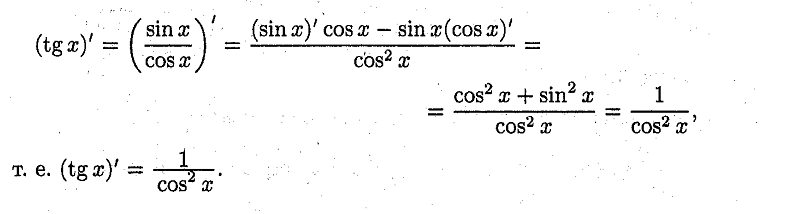
18. Правило вычисления производных от суммы , произведения,
частного функций.
Ответ:

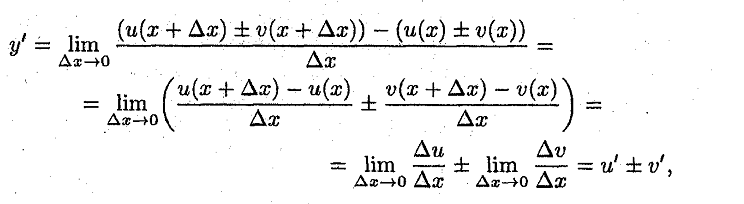
![]()

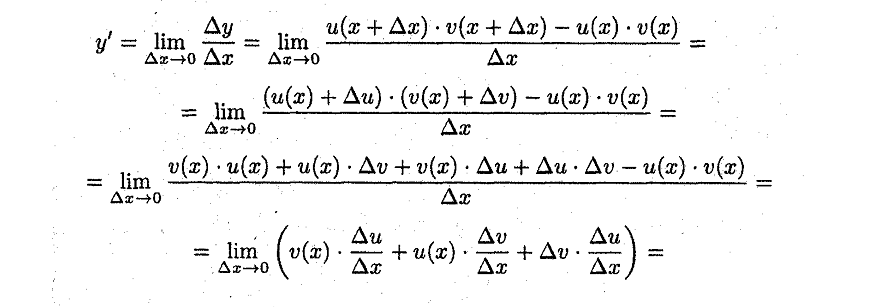
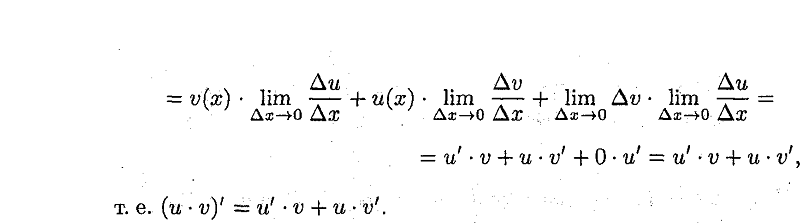


![]()
19. Производные высших порядков. Механический смысл второй производной.
Ответ:
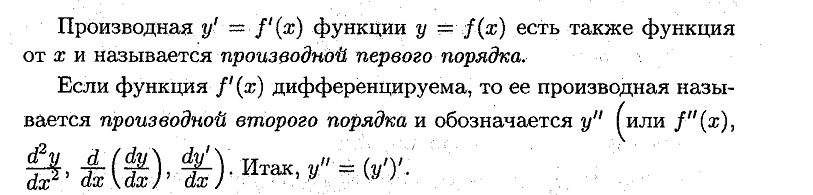

![]()
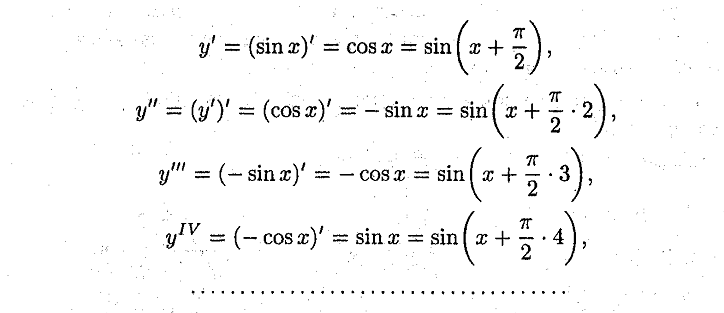
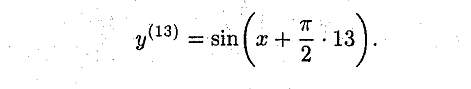
Механический смысл 2-й производной.


Вывод: производная 2 порядка выражает скорость, 3 порядка ускорение.
20.Теорема Ферма, геометрический смысл теоремы Ферма.
Ответ:
Если
функция ![]() имеет
производную и в точке
имеет
производную и в точке ![]() имеет
экстремум, то значение производной в
этой точке равно 0.
имеет
экстремум, то значение производной в
этой точке равно 0.
Доказательство
Пусть
-
точка минимума. Тогда при ![]() .
Значение выражения
.
Значение выражения 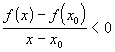 .
Значит,
.
Значит,  .
Рассмотрим теперь
.
Рассмотрим теперь ![]() ,
при этом также
,
при этом также ![]() ,
и выражение
,
и выражение 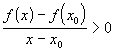 .
Значит, правая производная
.
Значит, правая производная 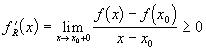 .
.
Следовательно
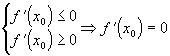 .
Теорема доказана.
.
Теорема доказана.
|
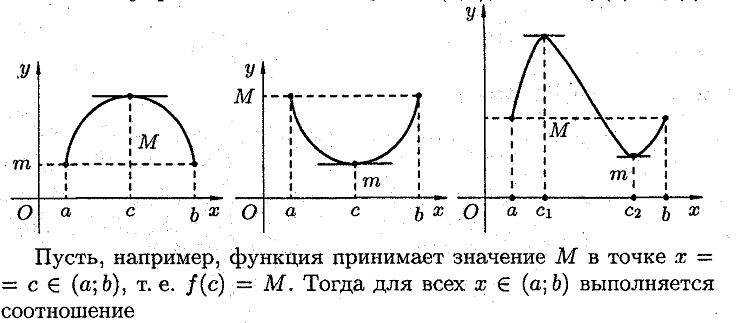
Геометрический смысл теоремы Ферма Существует такая точка , в которой касательная параллельна оси Ox. Замечания
|
Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример:
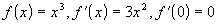 ,
но точка 0 - не экстремум.
,
но точка 0 - не экстремум.
21. Теорема Ролля , геометрический смысл теоремы Ролля.
Ответ:
![]()


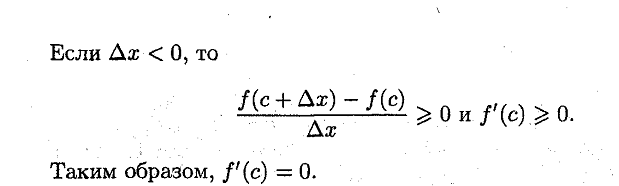

22. Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.
Ответ:
Теорема:
![]()
![]()
![]()
![]()
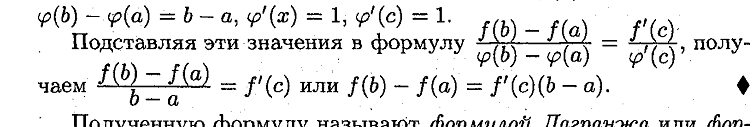

Геометрический смысл.


23. Многочлены Маклорена, Тейлора порядка N для функции имеющей производные N+1 порядка в данной точке. Примеры.
Ответ:
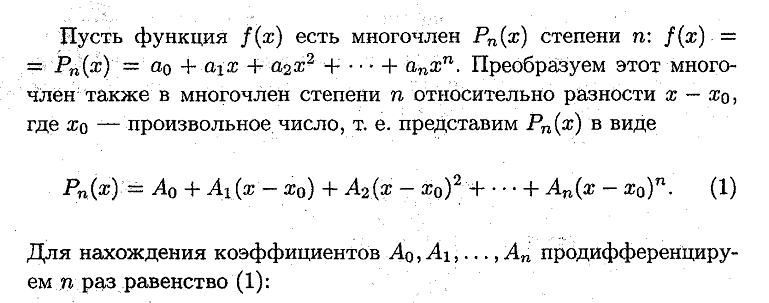

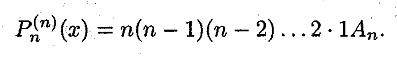


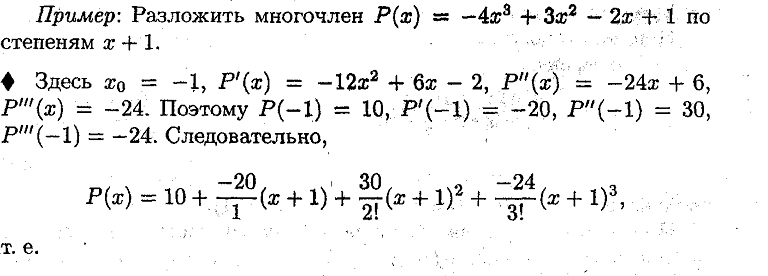
![]()



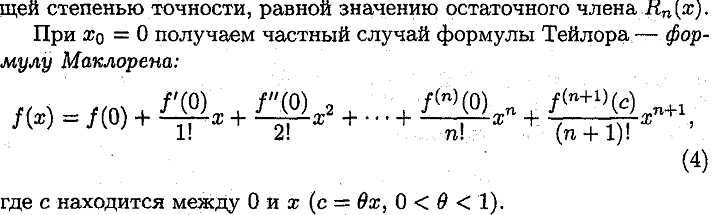

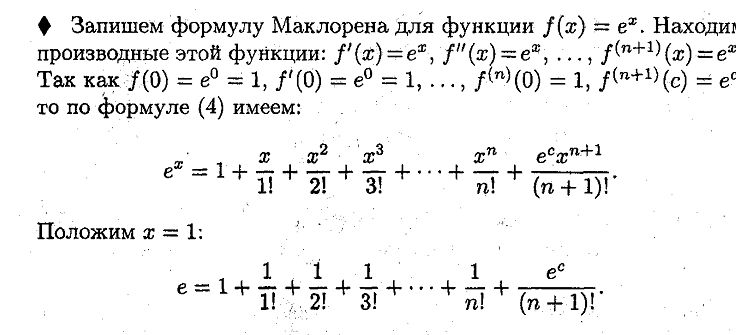


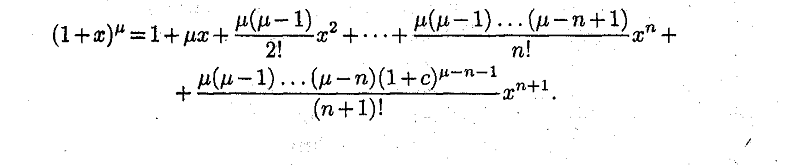
25.Достаточные условия возрастания (убывания) дифференцируемой функции на отрезке.
Ответ:
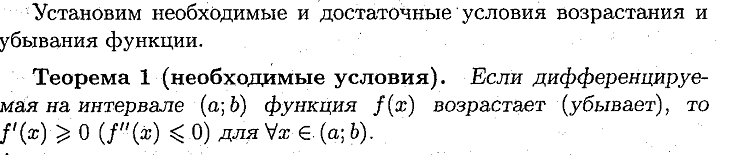
![]()
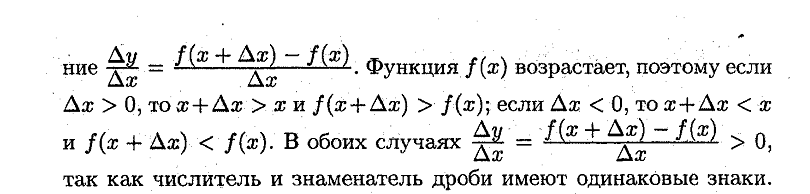



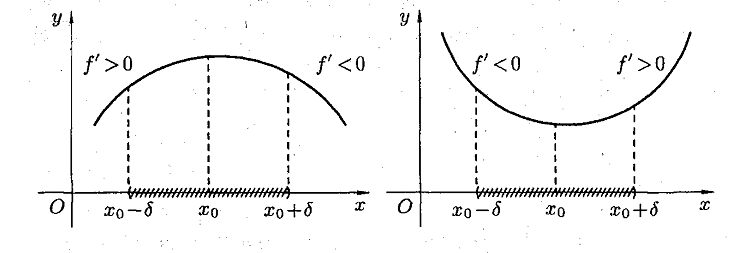
26. Понятие экстремума функции. Достаточное условие существование экстремума функции в точке.
Ответ:



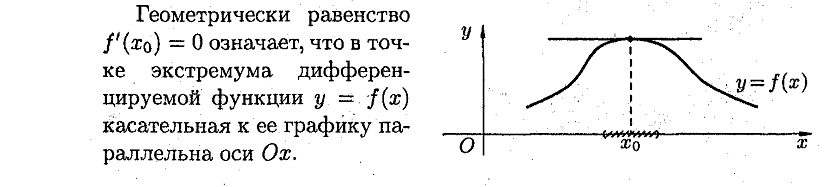







27. Понятие выпуклости вверх, вниз графика функции.
Точки перегиба.
Ответ:



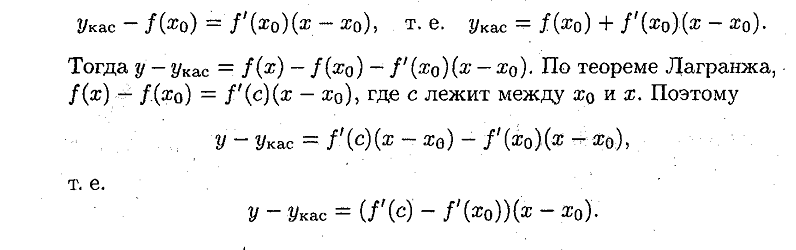
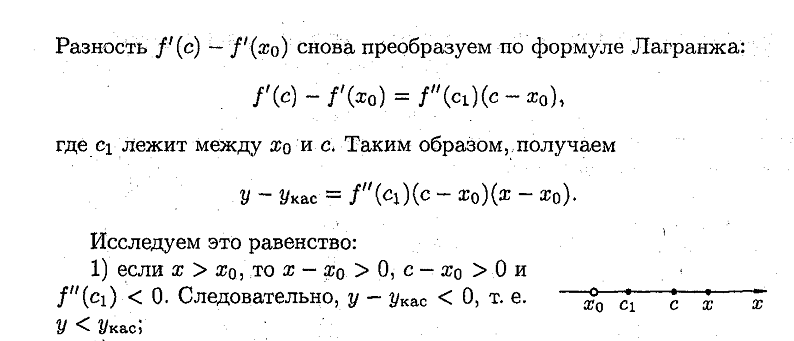



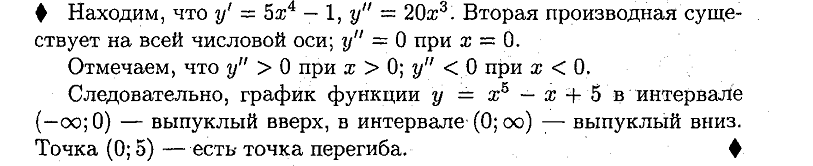
28. Нахождение пределов функции по правилу Лопиталя.

![]()

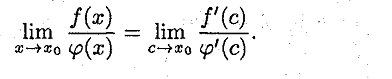

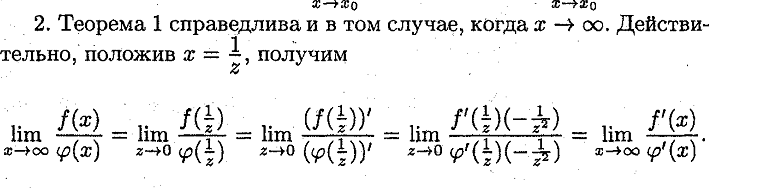
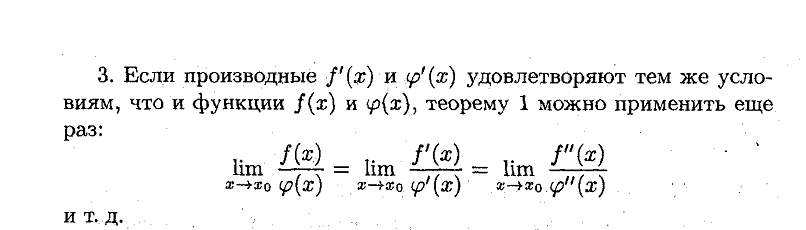
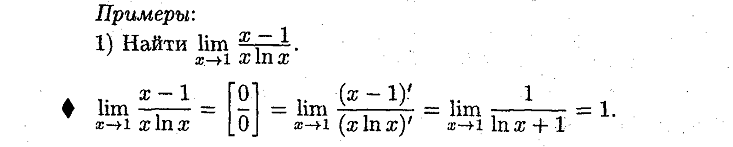




29. Понятие первообразной функции. Свойства первообразных.
Ответ:





![]()
Свойства:

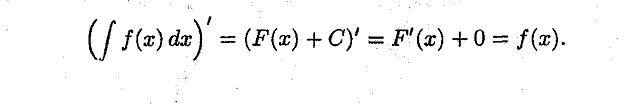
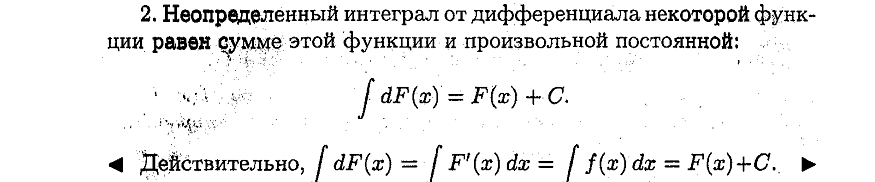

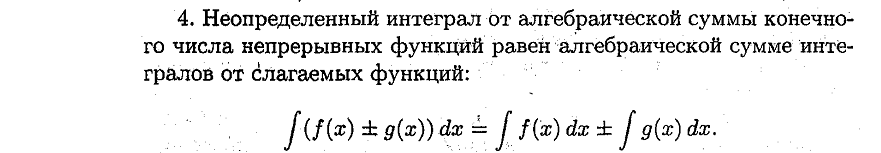
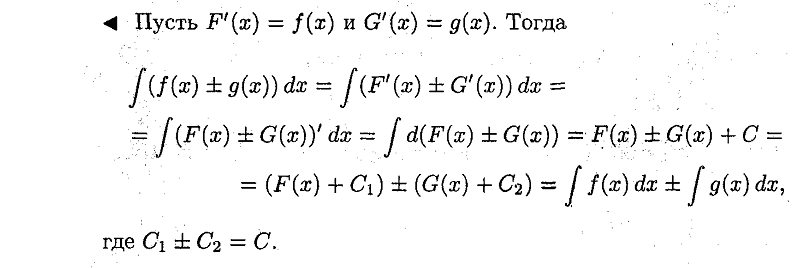


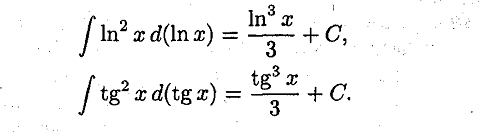
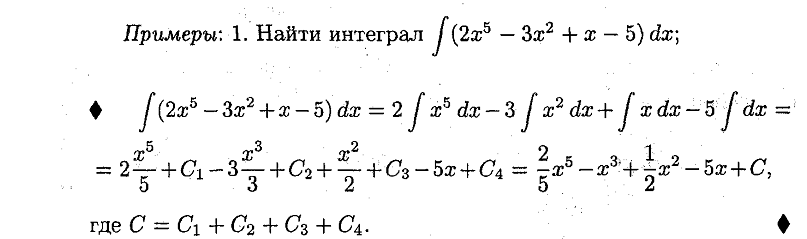
30. Понятие неопределенного интеграла. Понятие о неберущихся интегралах.
Ответ:


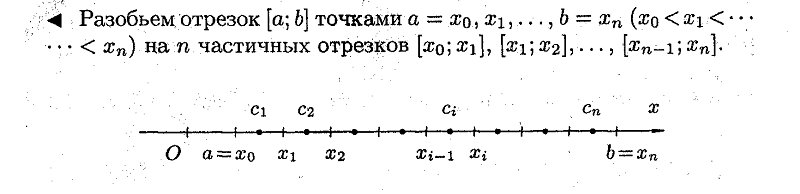
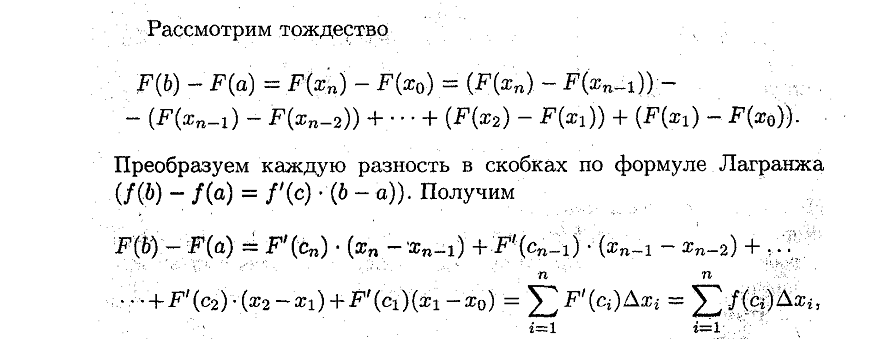
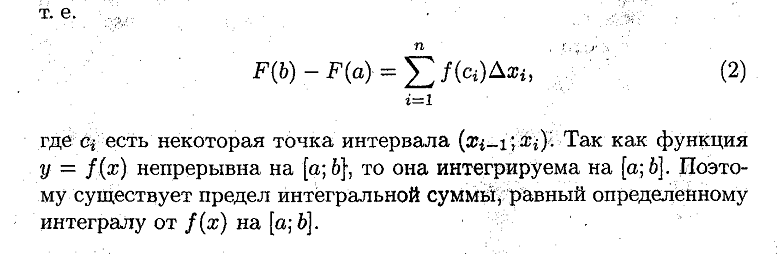





|