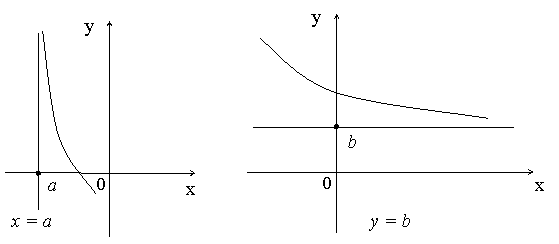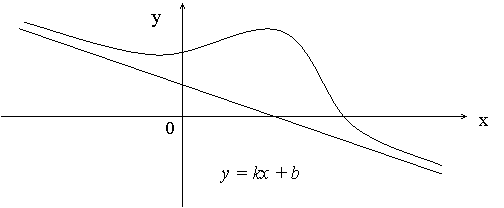9.Первый замечательный предел.
1
замечательный предел.
Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна
центральному углу Х, |BC| = tg x. Тогда
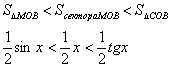
Разделим
все на
и
получим:
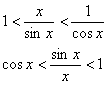
Т.к.
,
то по признаку существования пределов
следует
.
10. Понятие предела функции на бесконечности.
Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < . Запись этого факта:
Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < . Записывается это так:
11.Второй замечательный предел
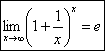
Пусть х→∞. Каждое значение х заключено между двумя положительными
целыми числами:
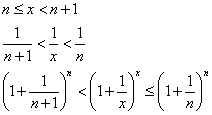
Если x→∞, то n→∞, тогда
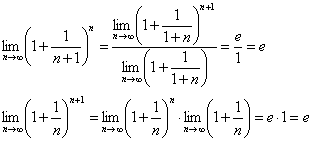
По признаку о существовании пределов:
12.Нахождение асимптот к графику функции.
Наклонные, горизонтальные и вертикальные асимптоты.
Ответ:
Определение. Асимптотой
графика функции 
называется
прямая, обладающая тем свойством, что
расстояние от точки 
графика
функции до этой прямой стремится к нулю
при неограниченном удалении точки
графика от начала координат.
По
способам их отыскания выделяют три вида
асимптот: вертикальные 
,
горизонтальные 
,
наклонные 
.
Очевидно, горизонтальные являются
частными случаями наклонных (при 
).
|
|
|
|
|
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема
1. Пусть
функция
определена
хотя бы в некоторой полуокрестности точки
и
хотя бы один из ее односторонних пределов
в этой точке бесконечен, т.е. равен 
или 
.
Тогда прямая
является
вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема
2. Пусть
функция
определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существует конечный предел функции 
.
Тогда прямая
есть
горизонтальная асимптота графика
функции
.
Может
случиться, что 
,
а 
,
причем 
и 
конечные
числа, тогда график имеет две различные
горизонтальные асимптоты: левостороннюю
и правостороннюю. Если же существует
лишь один из конечных пределов
или
,
то график имеет либо одну левостороннюю,
либо одну правостороннюю горизонтальную
асимптоту.
Теорема
3. Пусть
функция
определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существуют конечные пределы 
и 
.
Тогда прямая
является
наклонной асимптотой графика функции
.
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример.
Найдите все асимптоты графика функции 
.
Решение.
Функция
определена при 
.
Найдем ее односторонние пределы в
точках 
.
Так
как 
и 
(два
других односторонних предела можно уже
не находить), то прямые 
и 
являются
вертикальными асимптотами графика
функции.
Вычислим
(применим
правило Лопиталя) =
.
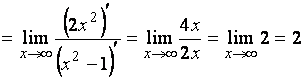Значит,
прямая 
горизонтальная
асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
Ответ:
график имеет две вертикальные асимптоты 
и
одну горизонтальную
.