13. Векторное произведение координатных ортов. Определение векторного произведения векторов, заданных своими координатами.
Ответ:
Векторное произведение координатных ортов.
Определение векторного произведения векторов, заданных своими координатами.
Пусть векторы а = (х1; у1; z1) и b = (х2; у2; z2) заданы своими координатами в прямоугольной декартовой системе координат О, i, j, k, причем тройка i, j, k является правой.
Разложим а и b по базисным векторам:
а = x1i + y1 j + z1 k, b = x2 i + y2 j + z2 k.
Используя свойства векторного произведения, получаем
[а; b] = [x1 i + y1 j + z1 k ; x2 i + y2 j + z2 k] =
= x 1x2 [i; i] + x1 y2 [i; j] + x1 z2 [i; k] +
+ y1 x2 [j; i] + y1 y2 [j; j] + y1 z2 [j; k] +
+ z1 x2 [k; i] + z1 y2 [k; j] + z1 z2 [k; k]. (1)
По определению векторного произведения находим
[i; i] = 0, [i; j] = k, [i; k]= — j,
[j; i] = — k, [j; j] = 0, [j; k] = i,
[k; i] = j, [k; j] = — i. [k; k] = 0.
Учитывая эти равенства, формулу (1) можно записать так:
[а; b] = x1 y2 k — x1 z2 j — y1 x2 k + y1 z2 i + z1 x2 j — z1 y2 i
или
[а; b] = (y1 z2 — z1 y2) i + (z1 x2 — x1 z2 ) j + (x1 y2 — y1 x2) k. (2)
Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами.
Полученная формула громоздка .Используя обозначения определителей можно записать ее в другом более удобном для запоминания виде:
Обычно формулу (З) записывают еще короче:
14.Нахождение площадей с помощью векторного произведения двух векторов.
Ответ:
По определению длина векторного произведения векторов равна
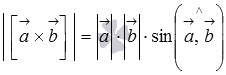
нам
известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла между
ними. Следовательно, длина векторного
произведения равна удвоенной площади
треугольника, имеющего сторонами векторы
и
,
если их отложить
от одной точки. Другими словами, длина
векторного произведения векторов
и
равна
площади параллелограмма со сторонами
и
и
углом между ними, равным
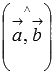
Пример:
В прямоугольной декартовой системе координат дан параллелограмм ABCD,
Используя векторное
произведение, определите площадь
треугольника АВD и площадь параллелограмма
АВCD.
Решение.
Обозначим
площадь треугольника АВD через
а площадь параллелограмма
. В геометрическом смысле длина векторного
произведения
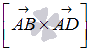равна площади параллелограмма АВCD, то
есть,
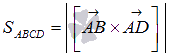, следовательно,
. Итак, решение задачи свелось к нахождению
длины векторного произведения.
Для
этого сначала определяем координаты
векторов
и
:
Теперь по их координатам находим векторное произведение
Вычисляем длину векторного произведения по его координатам .
Таким
образом,
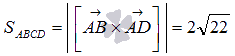и
.
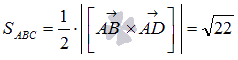Ответ:
15. Смешанное произведение векторов свойства, вычисление смешанного произведения через координаты векторов.
Ответ:
Смешанное
произведение записывают в виде:
.
Смысл смешенного произведения:
сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором.
Смешанное произведение представляет собой число – число.
Результат смешанного произведения – объем параллелепипеда, образованного векторами.
Свойства.
1. Смешанное произведение не меняется при циклической перестановке
сомножителей:
2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.
3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.
4. Смешанное произведение трех ненулевых векторов равно нулю тогда и
только тогда, когда они компланарны.
Три вектора называются компланарными, если результат смешанного произведения
равен нулю.
16. Векторные уравнения прямых.
