8. Проекция ( геометрическая , алгебраическая) вектора на ось. Свойства проекций.

Ответ:

Свойства проекций:

Свойства проекции вектора

Свойство 1.

Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:

Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.

Свойство 2. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:

Свойство 3.

Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:

9. Орт оси. Разложение вектора по координатным ортам. Координаты вектора. Свойства координат

Ответ:

Орты осей.

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

В трёхмерном случае орты обычно обозначаются

и Могут также применяться обозначения со стрелками и

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

Разложение вектора по координатным ортам.

Орт координатной оси обозначается через , оси - через , оси - через (рис. 1)

Для любого вектора который лежит в плоскости имеет место следующее разложение:

Если вектор расположен в пространстве, то разложение по ортам координатных осей имеет вид:

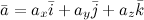
Координаты вектора:

Чтобы вычислить координаты вектора , зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1).

Свойства координат.

Рассмотрим координатную прямую с началом координат в точке О и единичным вектором i. Тогда для любого вектора a на этой прямой: a = axi.

Число ax называется координатой вектора a на координатной оси.

Свойство 1. При сложении векторов на оси их координаты складываются.

Свойство 2. При умножении вектора на число его координата умножается на это число.

10. Скалярное произведение векторов. Свойства.

Ответ:

Скалярным произведением двух ненулевых векторов называется число,

равное произведению этих векторов на косинус угла между ними.

Свойства:

1. Скалярное произведение обладает переместительным свойством: ab=bа

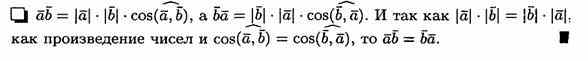
11. Скалярное произведение координатных ортов. Определение скалярного произведения векторов, заданных своими координатами.

Ответ:

Скалярное произведение (×) орты

(X)	I	J	K
I	1	0	0
J	0	1	0
K	0	0	1

Определение скалярного произведения векторов , заданных своими координатами.

Скалярное произведение двух векторов и заданных своими координатами, может быть вычислено по формуле

12. Векторное произведение двух векторов. Свойства векторного произведения.

Ответ:

Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую., если нет то в противоположном ( показать как он показывал с «ручками»)

Векторным произведением вектора а на вектор b называется вектор с который :

1. Перпендикулярен векторам а и b

2. Имеет длину, численно равную площади параллелограмма, образованного на a и b векторах

3. Векторы, a ,b, и c образуют правую тройку векторов

Свойства:

1.

2.

3.

4.