12.Предельная норма замещения в теории производства.

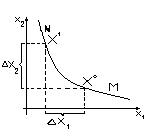
Пусть MN является классом равноценности и пусть у индивида есть первоначальный набор товара x⁰ = (x₁⁰, x₂⁰). Из рисунка видно, что уменьшение потребления первого вида товара на величину Δ x₁ можно компенсировать увеличением второго вида товара на величину Δ x₂. Компенсация означает, что набор товаров x¹ = (x₁¹-Δ x_1, x₂¹+Δ x₂) имеет туже ценность для потребителя, что и набор товаров x⁰. Т.е. обе точки находятся в одном классе равноценности.

Проводя рассуждения аналогичные как и для функции полезности с полным соотношению 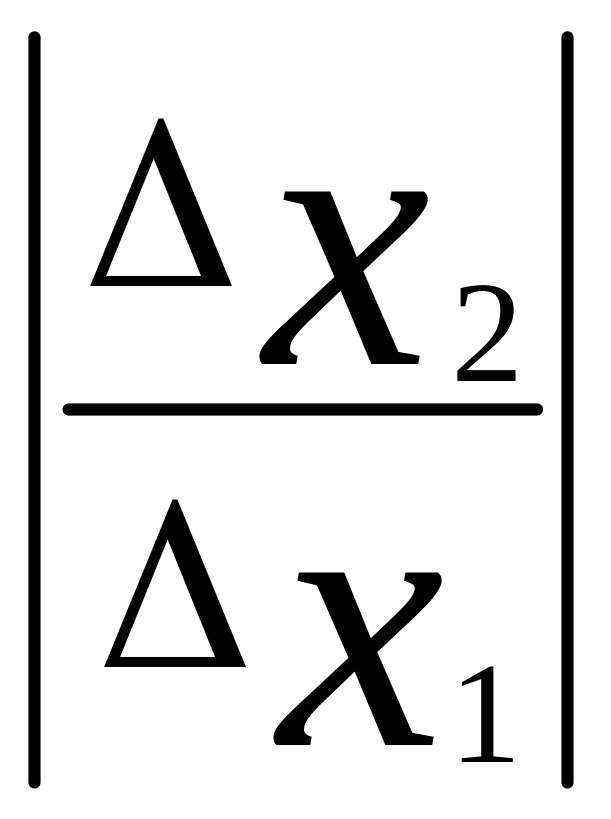, которое показывает сколько единиц второго товара могут компенсировать уменьшение первого товара на единицу. Т.к. Δ x₁ < 0, Δ x₂ > 0, то последнее соотношение запишется в виде .

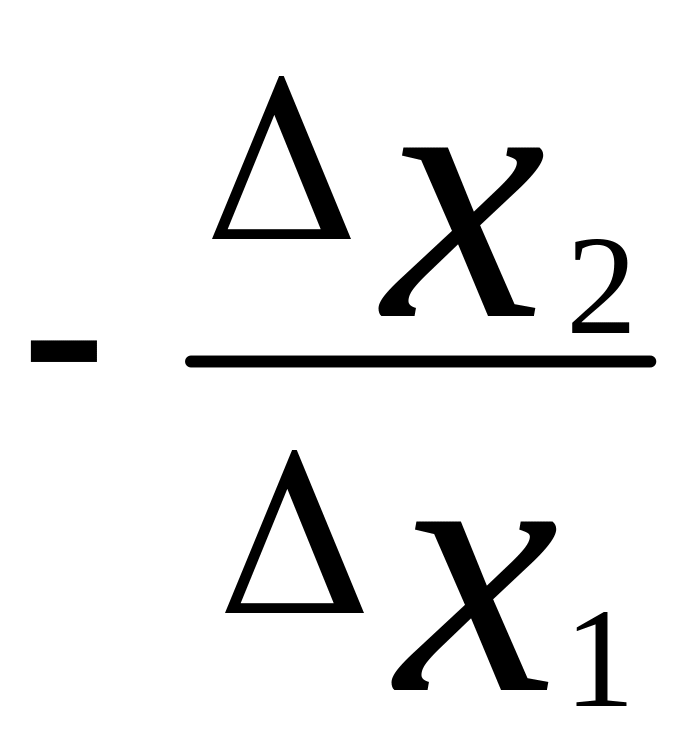Переходя к пределу в данном соотношении получаем величину, называемую предельной нормой замещения первого товара вторым.

Предельное соотношение вида 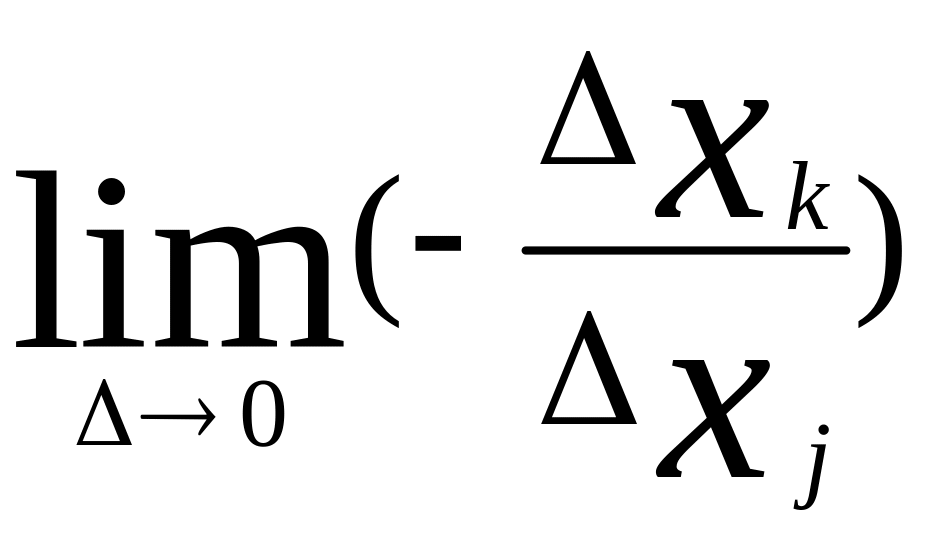называется предельной номой замещения j-го товара k-ым и обозначается M_j^k.

Т.к. при передвижении в одном классе равноценности полезность не изменяется, то выполняется

.

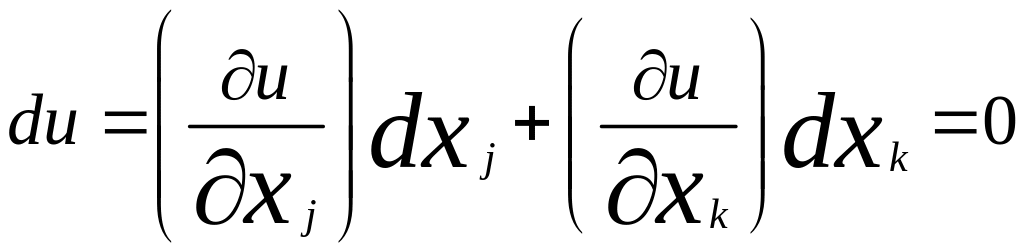Из которого получаем

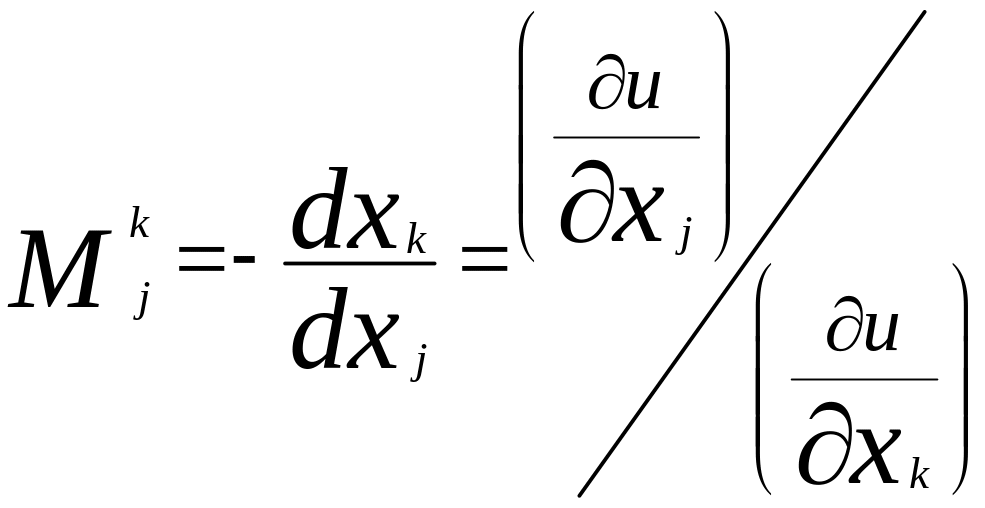
Т.е. предельная норма замещения равняется отношению предельных полезностей товара.

13. Математические модели задачи фирмы.

Пусть фирма производит один вид продукта, используя видов ресурсов: . Известна производственная функция . Пусть также цена выпускаемой продукции; цена го ресурса, . Доход от реализации готовой продукции .

Общие выплаты на все вида затрат на ресурсы составят величину в размере и называются переменными издержками, т.к. связаны с объемом выпускаемой продукции. Кроме того, фирма несет и постоянные издержки , которые связаны с расходом на содержание фирмы. Тогда общие издержки составят:

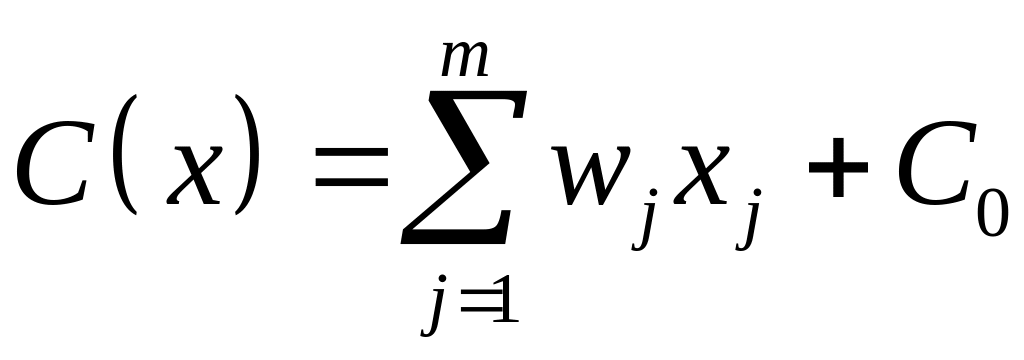
Замечание: Т. к. постоянные издержки не связаны с выпуском, то при построении краткосрочных моделей их не учитывают.

Тогда общий результат производства «затраты – выпуск» можно оценить величиной

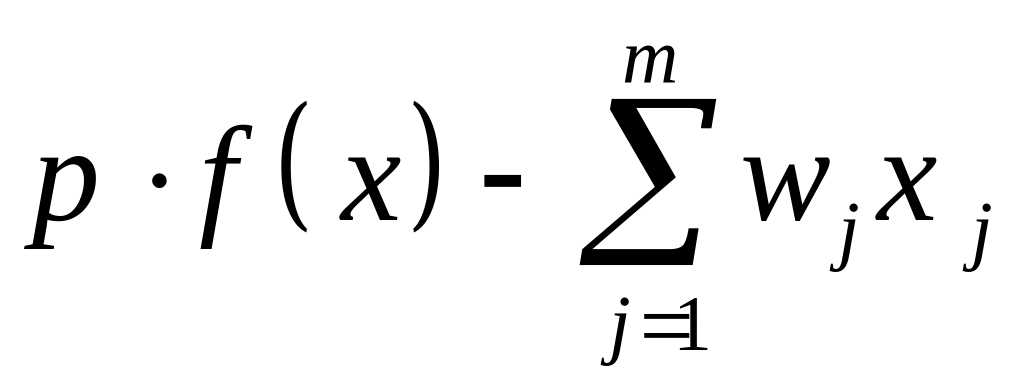
Если эта величина, то пара приносит прибыль, в противном случае - убыток.

С помощью полученных формул построим математические модели различных задач фирмы.

1. Долгосрочная задача. На долгосрочный период фирма может планировать любые затраты, поэтому модель имеет вид: 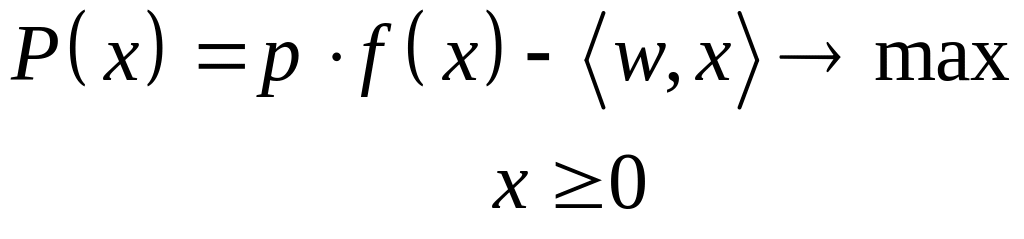(1)

В задаче (1) постоянные издержки не учтены, т.к. они не влияют на максимизацию прибыли по переменным затратам .

2. Краткосрочная задача. Планируется с учетом наличных на данный период запасов ресурсов, поэтому ее модель строится на условную оптимизацию

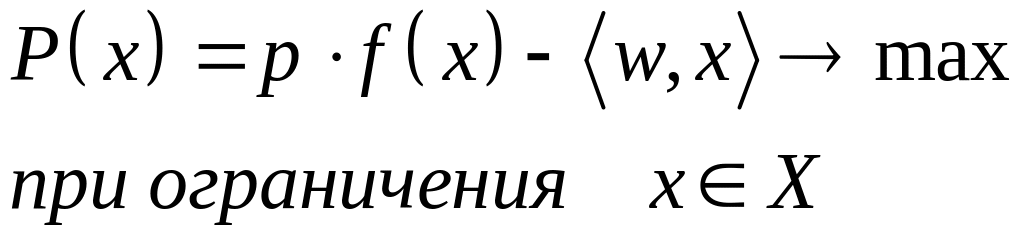(2)

где множество может иметь вид:

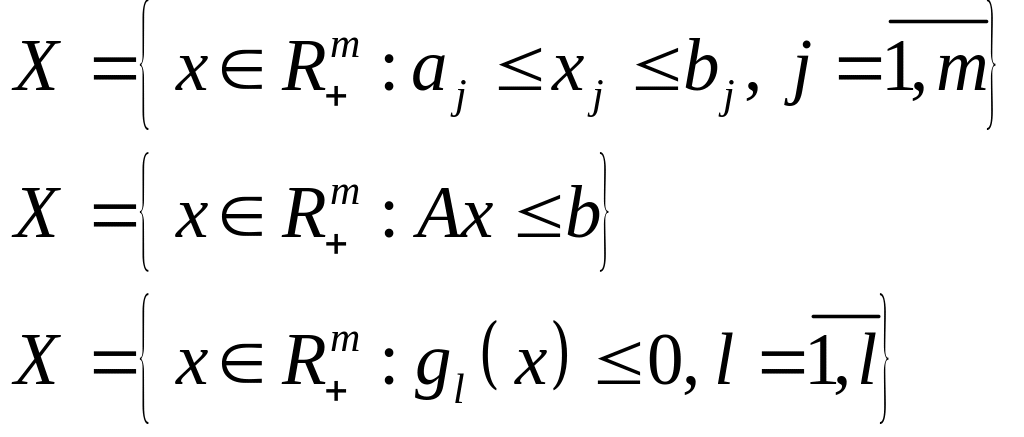
3. Задача многопродуктового производства. Пусть фирма выпускает 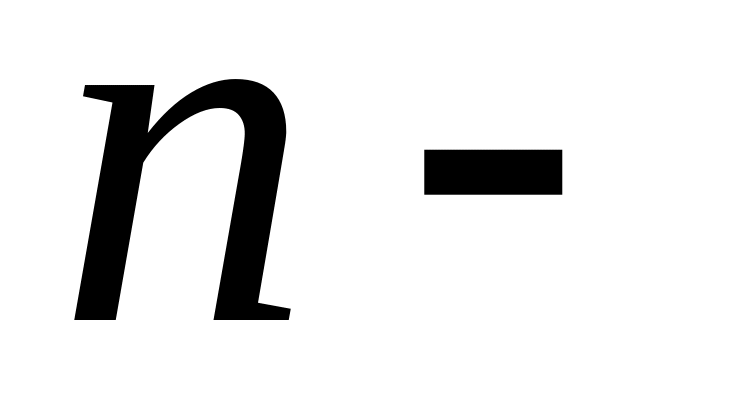видов продукции и для 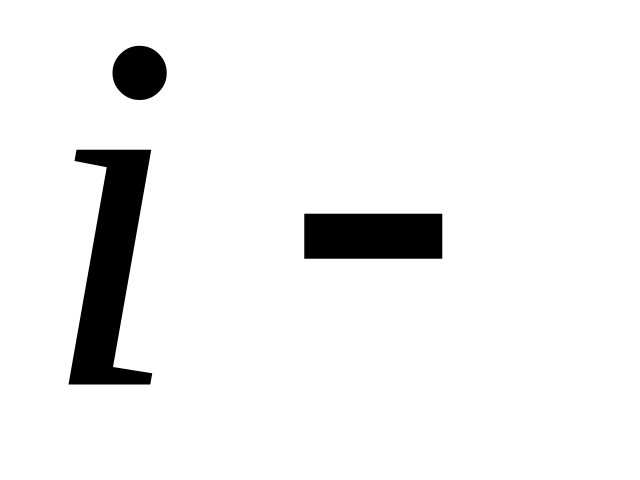го продукта известны: производственные функции 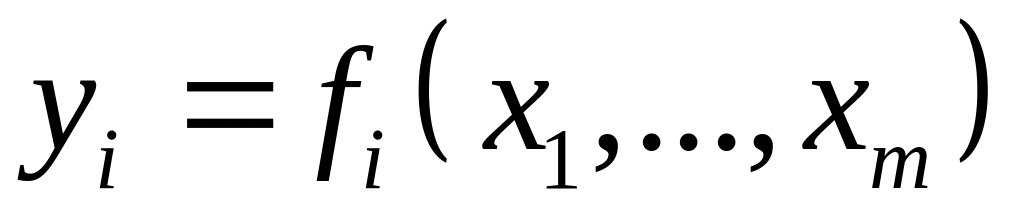и цена . Для каждого го вида ресурса известны функции 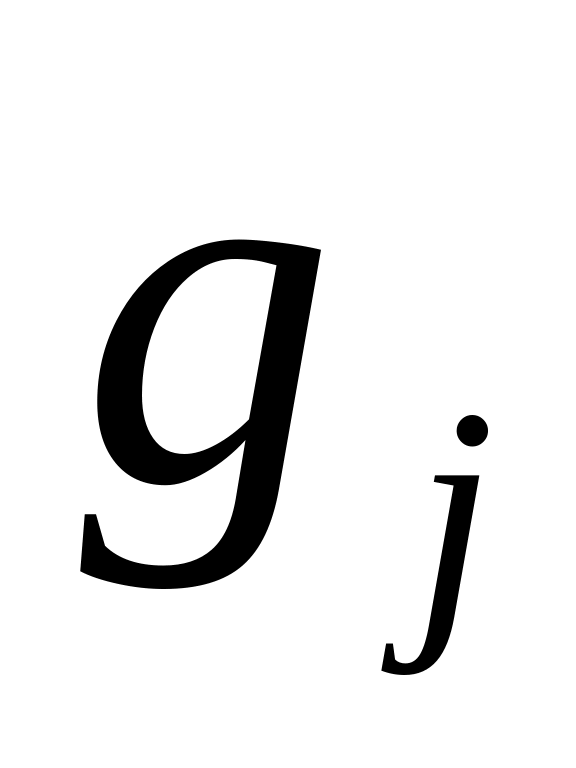, описывающие суммарные затраты этого ресурса для производства всех видов продуктов, и его наличное количество 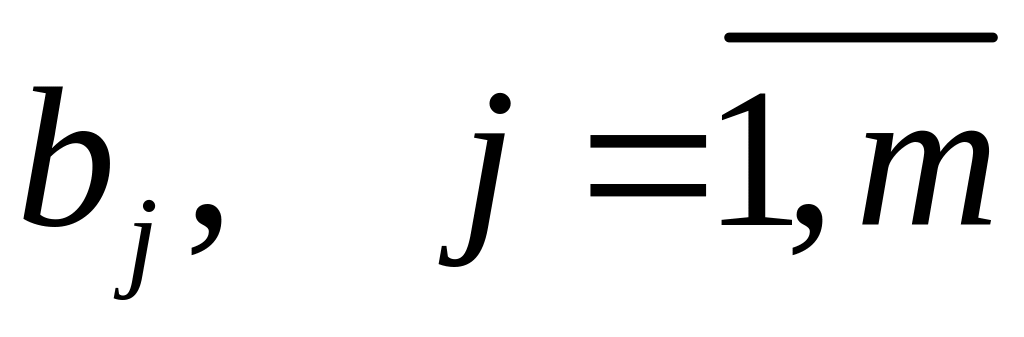. В этом случае, модель долгосрочной задачи 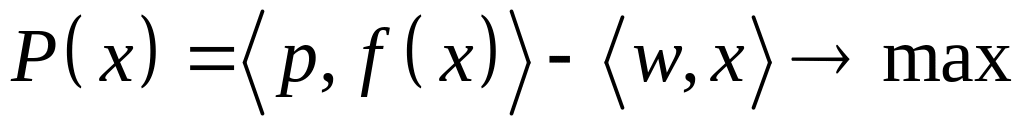краткосрочная задача 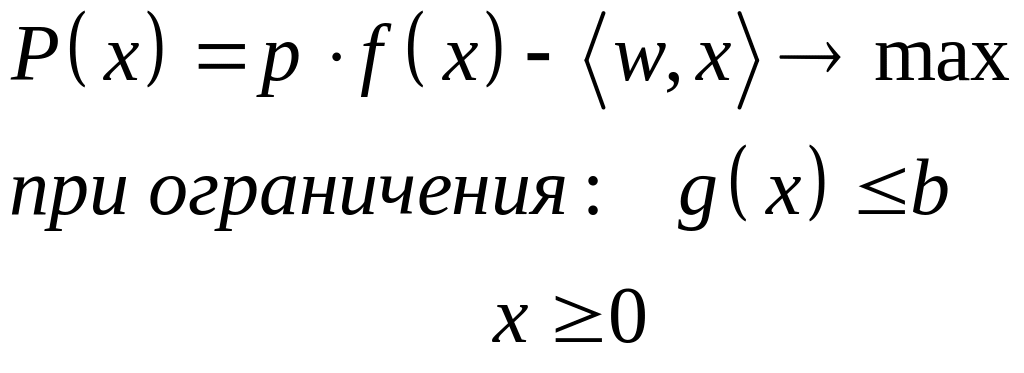(3)

где вектор цен выпускаемых товаров, вектор-функция затрат, вектор наличных запасов ресурсов.

4. Задача на минимизацию затрат. Пусть фирма планирует выпуска продуктов в объемах , т.е. рассматриваются фиксированные объемы выпуска. В этом случае оптимизационная задача имеет вид

Если требуется перевыполнить план выпуска, ограничения заменяются ограничениями