6.Решение задачи потребителя в случае двух товаров.

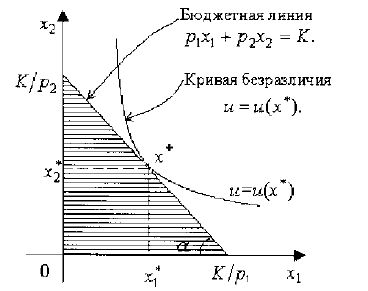
Наклон бюджетной линии равен Наклон кривой безразличия , находится из выражения , т.е. . Так как в точке наклон кривой безразличия равен наклону бюджетной линии, то т.е. то есть в оптимальном наборе товаров предельная норма замещения товара i товаром j оценивается отношением их цен (то есть зависит исключительно от их цен).

7. Функция спроса и ее свойства.

Опр: Пусть множество допустимых наборов товаров для потребления, множество пространство цен. Тогда функцией спроса индивидуального потребительского выбора называют такое отображение , которое каждой паре ставит в соответствие множество наиболее предпочтительных наборов товаров, т.е. где множество всех подмножеств множества Перепишем соотношение (1) в другой форме:

Опр: Любая точка называется спросом при текущих ценах и доходах.

Задача потребителя :

Функция спроса определяется следующим образом:

тогда функция спроса

Свойства функции спроса:

1. однородность нулевой степени.

Опр: Если для функция спроса вида , то функция спроса является однородной нулевой степени относительно всех цен и доходов.

2. Для функции спроса однородной нулевой степени объем потребления зависит не от цен и дохода, а от отношения цен и отношения дохода к ценам.

Пусть тогда, выбирая в качестве эталона 1-ый товар, получаем, что функцию спроса можно зависать в следующем виде: где относительная цена, а реальный доход.

Часто на практике используют коэффициент пропорциональности: в нашем случае .

8.Основное матричное уравнение теории потребления. Уравнение Слуцкого.

Перепишем основное матричное уравнение в виде

Решение данной системы относительно показателей сравнительной статистики по спросу имеет вид:

где обратная матрица Гессе, а - коэффициент убывания предельной полезности денег. Сравнивая (2) и (3) запишем, что

Сравнивая это уравнение с (1) получаем (**)

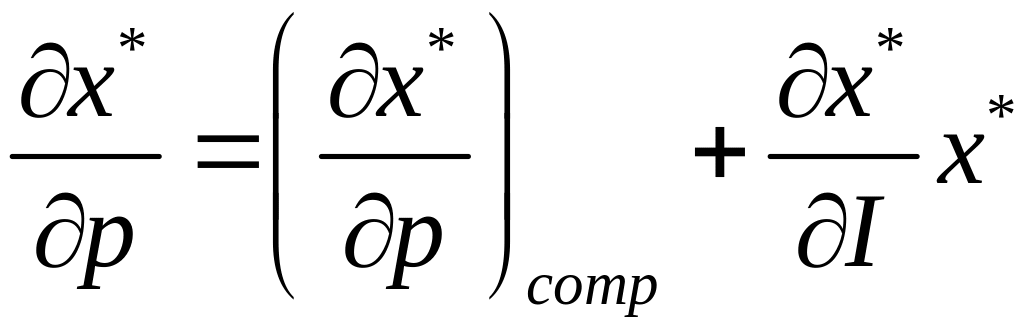
Данное равенство называется уравнением Слуцкого. В координатной форме уравнение Слуцкого выглядит так

где левая часть – общий эффект от влияния цены на спрос; первое слагаемое в правой части – влияние замены, т.е. компенсированное изменение цены на спрос; второе слагаемое – влияние дохода – влияние изменения дохода на спрос. Перепишем уравнение следующим образом:

Из (4) следует, что матрица влияния замены симметрична и отрицательно определена. Из отрицательной определенности следует (5).

т.е. компенсированное изменение цены товара приводит к уменьшению спроса на этот товар. Из симметричности матрицы влияния замены и уравнения (4) получаем

Поэтому уравнение Слуцкого в частности показывает, что

Здесь производная называется влиянием на спрос (на j-ый товар) изменения частной цены (цены j-го товара).

9. Основное матричное уравнение теории потребления. Типы товаров.

(*)

Элементы уравнения – показателями сравнительной статистики.

Типы товаров:

• Товар с номером j наз-ся нормальным, если ,

т.е. спрос растет – цена падает.

• Товар называется товаром Гиффина(ТГ), если ,

т.е. спрос растет - цена растет.

• Товар называется ценным, если - ,

т.е. доход потребителя растет – спрос растет.

• Товар называется малоценным, если ,

т.е. доход потребителя растет – спрос падает.

Два товара i и j называются взаимозаменяемыми, если (с ростом цены на j, спрос на i увеличивается) и взаимодополняемыми, если .

Как следует из соотношений (**) и , следует , т.к. , то:

1. 1. если товар явл-ся ТГ, то он обязательно малоценный;

2. 2. если ценный, то обязательно нормальный.

Каждый товар попадает в одну из следующих категорий:

1. 1. нормальный и ценный;

2. 2. нормальный и малоценный;

3. 3. ТГ и малоценный.

(!) Существование ТГ кажется не вполне реальным. Действительно, его определение противоречит закону о спросе. Однако, когда какой-либо популярный среди населения товар продается по слишком низкой цене, появляется подозрение о его качестве. Это может оказаться причиной снижения спроса на него. Последующее же поднятие цены может повысить спрос на этот товар.

Умножим обе части равенства

на вектор цен p , получим:

Следовательно, в координатной форме получаем , где все

Так как и в силу неравенства (**) следует, что для каждого j-ого товара существует такой i-ый товар ( ) для которого .

Т.о. в наборе каждому товару соответствует по крайней мере один товар, который составляет с ним взаимозаменяемую пару.