28. Экономика благосостояния и оптимум Парето.

Пусть предпочтения потреблений выпуклы, непрерывны и локально-ненасчщаемы. Технологические множества каждого производителя выпуклы и, по крайней мере, одно из них удовлетворЯет свойству свободы расходования. Тогда если - оптимальные состояния по Парето причем (нулевйо вектор), . Тогда сущест. такой вектор цен Р, что тройка величин явл. равновесием Вальраса.

Задача о нахождении оптимального решения Парето.

Пусть предпочтение потребителей задается непрерывными функциями полезности. Сопоставим каждому потребителю число , причем для данных чисел

Введем в рассмотрение совокупную функцию полезности

И задачу о нахождении оптимума Парето

- ограничения

Теорема 1) Пусть - решение задачи (4). Тогда данная точка А если величины , то тогда

2) Пусть функции полезности является непрерывными и вогнутыми, а технологические множества - выпуклы. Тогда, если точка , то сущ такие величины , что точка будет решением задачи (4)

Док-во: 1) Пусть точка явл решением задачи 4 и не ю Тогда существует такое допустимое состояние экономики , которое удовлетворяет неравенству:

По определению функции получаем, что совокупная функция полезности -

Тем самым получаем противоречие. ТО точка явл решением задачи 4

29. Модель конкурентного равновесия с фиксированными доходами.

Рассм мод, когда доходы не зависят от цен, т.е. явл пост-ми. Такая мод наз мод-ю с фиксир-ми доходами. В этом случ закон Вальраса для совокуп спроса и совокуп предложения может выполняться не при всех ценах р. Пусть эк-ая сис-ма сост из l потребтелей и m товаров, -ф-ии полезности потребителей, -мн-ва, на к-ых определены ф-ии полезности, -фиксир доход j-го потребителя, Y-совокуп технологическое мн-во, -ф-ия спроса j-го потребителя:

, где ,

-ф-ия совокуп спроса, S(p)-ф-ия совокуп предлож-я

.

Теорема(Полтеровича) Пусть вып-ся усл-я: 1)ф-ия непр-ны и вогнуты на . 2)Мн-ва , содер-ие нулевой в-р, замк и выпукл 3) 4)Y-выпуклый компакт, причем 5)Существуют . Тогда в мод с фиксир дох существует конкурентное равновесие.

Отличия от т. Эрроу-Дебре:

• Не требуется насыщенность потребителей

• Нет никаких условий отн-но стр-ры мн-в

• Предполаг, что все в-ры совокуп технологич мн-ва неотрицательны.

Пусть , где

. Совокупность в-ов (р*,х*,у*) – наз сост-ем конкурент полуравновесия, если вып-ся усл-я: ,

, , , где E(p)=D(p)-S(p)-ф-ия избыточ спроса. Обозначая , получим, что если , то сост полуравновес в опред-м выше смысле стан-ся сост равновесия в классическом смысле. Существование полуравн-я для лин мод дают алг-мы отыскания полуравновесных цен.

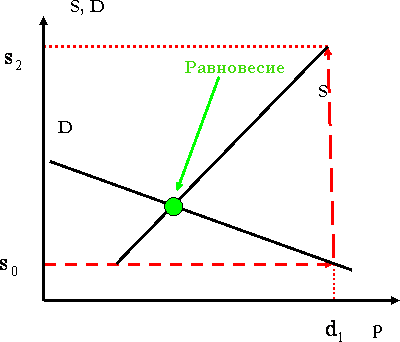
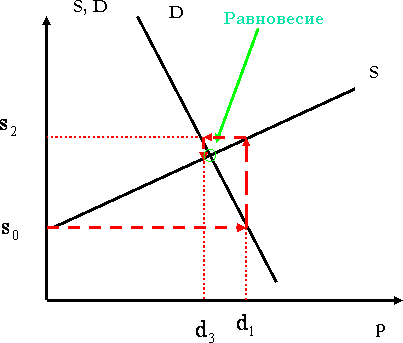
30.Алгоритмы формирования цен. Паутинообразная модель.

Рассмотрим некий товар. Если спрос на этот товар будет превышать предложение, то продавец будет повышать цену товара, а если предлож. будет превышать спрос, то продавец будет эту цену снижать. Этот процесс будет продолжаться до тех пор, пока не будет установлена такая цена, при которой объем спроса на товар будет равен объему предложения или, иначе говоря, не будет достигнуто рыночное равновесие. Рыночным равновесием назыв. ситуация когда общее кол-во каждого товара, который индивид хочет купить по текущим ценам, совпадает с предложением этого товара на рынке.

Основными задачами теории рыночного равновесия являются:

1. Существование рыночного равновесия. 2. Единственность рыночного равновесия. 3. Устойчивость рыночного равновесия.

Паутинообразная модель: Рассмотрим модель перехода рынка в состояние равновесия. Предполагается, что рынок описывается с помощью кривых спроса и предложения товара. Кривая предложения представляет собой зависимость предложения товара от его текущей рыночной цены Очевидно, что зависимость является неубывающей функцией своего аргумента. Кривая спроса представляет собой зависимость спроса на товар от его текущей рыночной цены Очевидно, что зависимость является невозрастающей функцией своего аргумента. Для простоты выкладок будем предполагать, что функции спроса и предложения являются линейными, т. е.: Найдем равновесную рыночную цену: . Паутинообразная модель, перехода рынка в состояние равновесия получается из следующих соображений. Разобьём всю ось времени на равные промежутки и пронумеруем их 0,1,2,3,... .Будем считать, что длительность этих промежутков равна длительности цикла производства. На интервале продается товар, произведенный на интервале На этом интервале его было произведено На интервале его продавали по цене и спрос был Считая, что спрос равен предложению, получаем:

Выражение, стоящее в квадратных скобках представляет собой сумму первых членов геометрической прогрессии с основанием равным 1 и знаменателем Имеем:

Возможны следующие ситуации: 1.Стабилизация рынка. Это произойдет в случае, когда . В этом случае и система со временем осуществит переход в точку рыночного равновесия. Изобразим процесс перехода рынка в равновесное состояние на графике:

2. Рынок будет испытывать циклы роста и спада производства. Это будет происходить в том случае, когда . В этом случае и рыночная цена будет совершать колебания равной амплитуды вокруг точки рыночного равновесия. Эти колебания являются прообразом экономических циклов роста и спада производства.

3. Дестабилизация рынка. Это произойдет в случае, когда . В этом случае и амплитуда колебаний рыночной цены вокруг точки равновесия будет возрастать, что в конечном итоге приведет к краху рынка.