26. Модель Эрроу-Дебре. Лемма Гейла.

Введем для каждого j-го производителя множество , которое, в отличие от модели Вальраса, трактуется как множество производственных планов (а не оптимальных планов), т.е. это есть множество мерных векторов , часть компонент которых описывает затраты, а другая часть — соответствующие этим затратам выпуски товаров. Компоненты, соответствующие затратам, как и в модели Вальраса, идут с отрицательными знаками. Поэтому скалярное произведение показывает прибыль, полученную -ым производителем в результате реализации плана . Тогда оптимальный план , участвующий в определении совокупного предложения, определяется как решение задачи: , (1) Оптимальное решение этой задачи обозначим через , а множество всех таких решений (множество оптимальных планов) — . Если задача (1) имеет единственное решение, то .Доход -потребителя складывается следующим образом. Пусть коэффициент , который показывает долю -го потребителя в прибыли -го производителя. Предполагается (как и в модели Вальраса), что прибыль каждого производителя делится между всеми потребителями полностью, т.е. Пользуясь коэффициентами , суммарные дивиденды , получаемые ым потребителем от производственного сектора 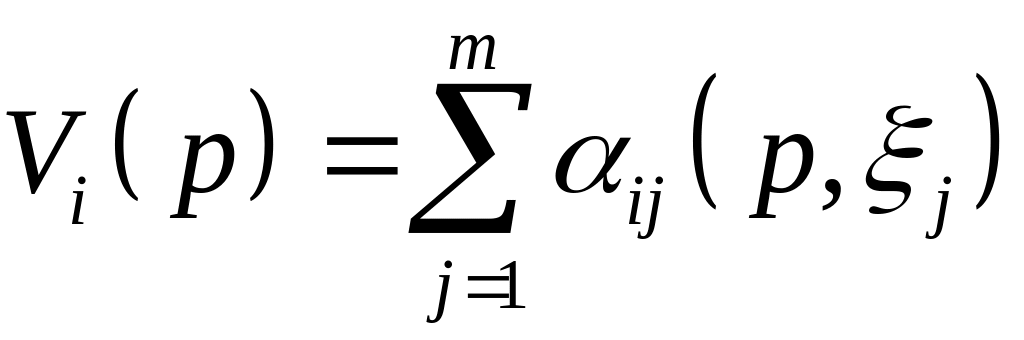, где . Поэтому, общий доход го потребителя при реализации производственных планов , вычисляется по формуле:

Функция спроса потребителя конкретизируется следующим образом. Вводится множество допустимых векторов потребления , а предпочтение потребителя на этом множестве задается с помощью функции полезности . В результате вектор-функция спроса (как и в теории потребления), строится как решение задачи:

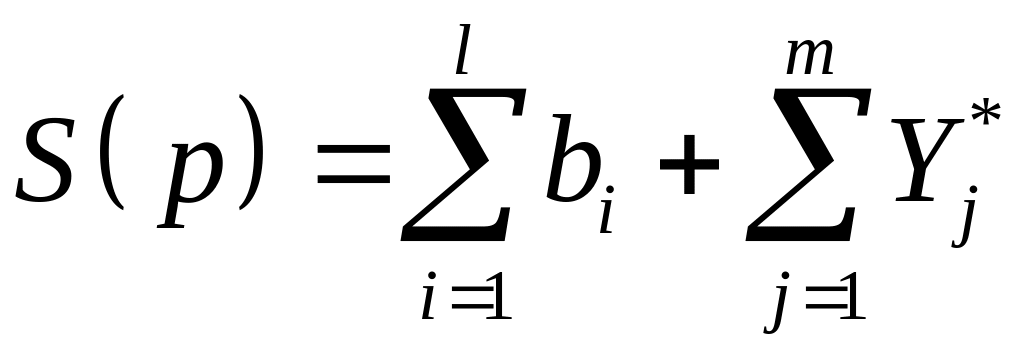(2) Оптимальное решение задачи (2) обозначим через , а множество всех таких решений– . Если (2) имеет единственное решение, то . Таким образом, виды множеств в правых частях соотношений (3) и (4) определяющих функции совокупных спроса и предложения следующие: (3) (4)

Модель рынка , в кот. ф-ции определены в виде (3) и (4), наз-ся моделью Эрроу-Дебре, если вып-ны след. требования:

1. Мн-во 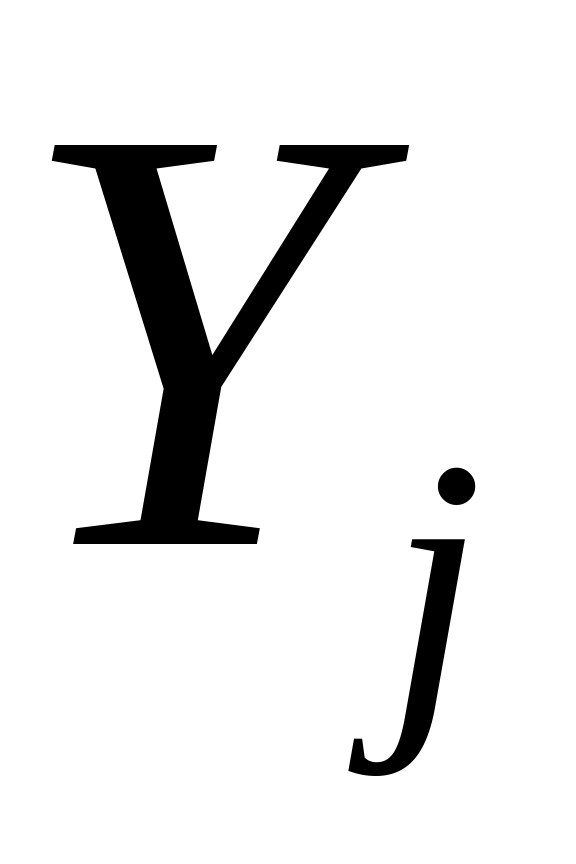компактно в 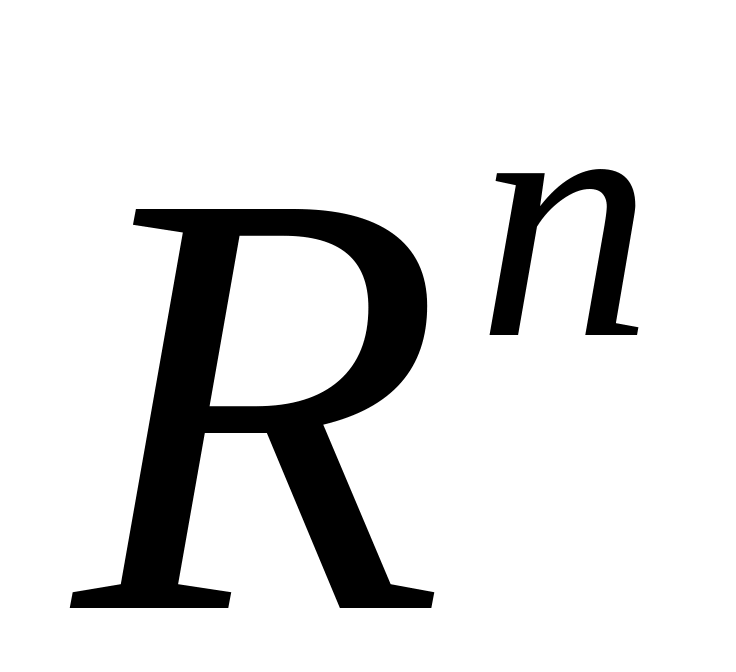и содержит нулевой вектор .

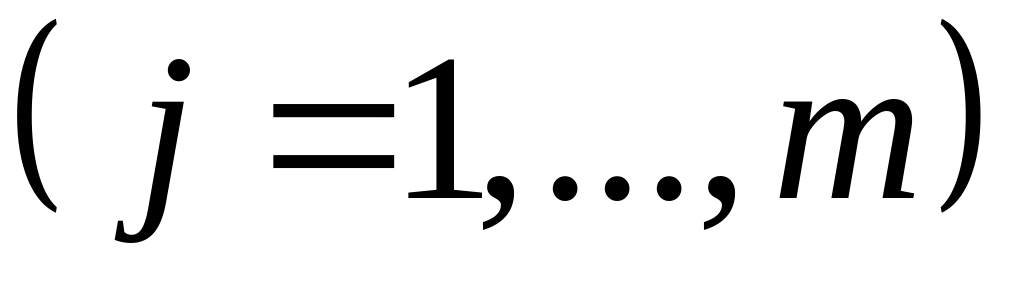2. Множество выпукло в .

3. Мн-во 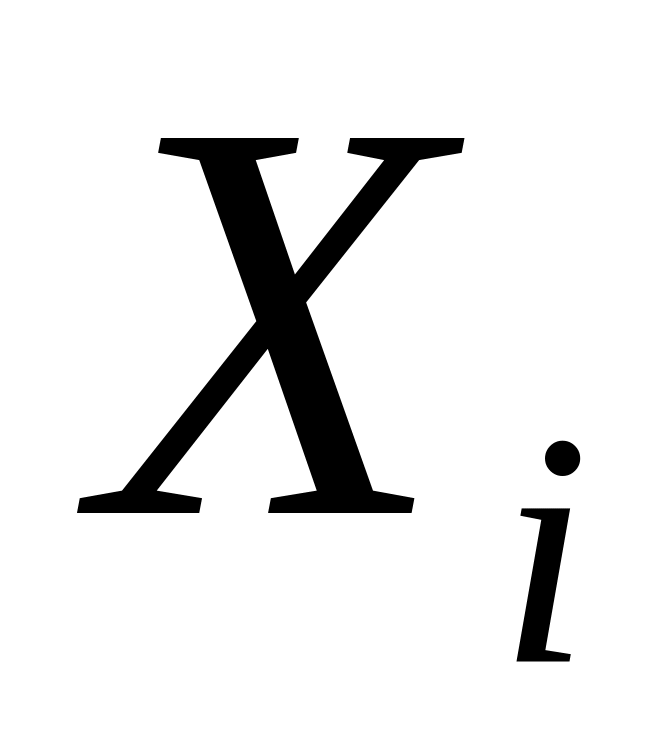зам-то и выпукло в причем, если 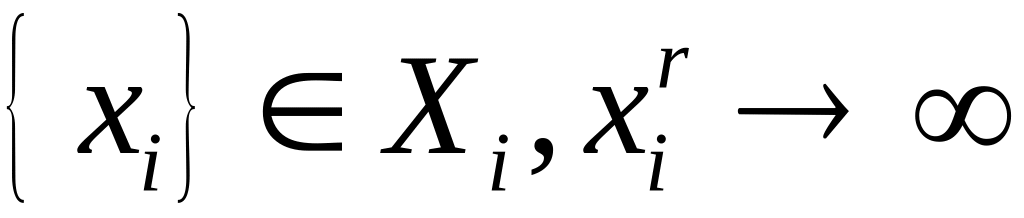для , то для всех .

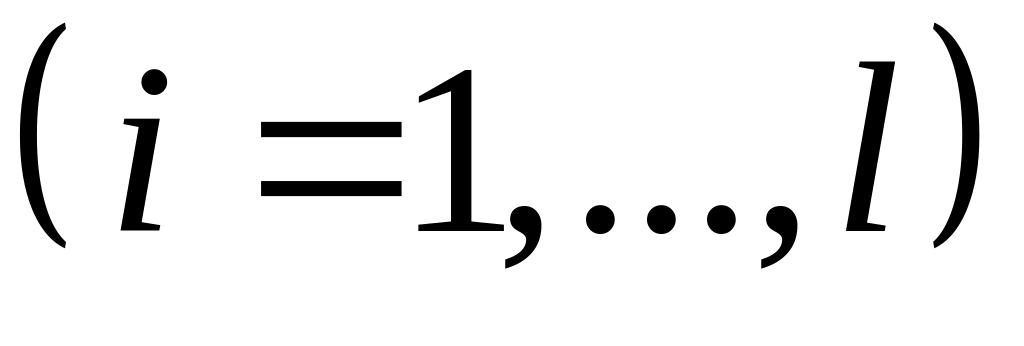4. Ф. пол-сти непр-но диф-ма на и строго вогнута .

5. Функция обладает свойством ненасыщаемости .

6. Существует , для которого ,

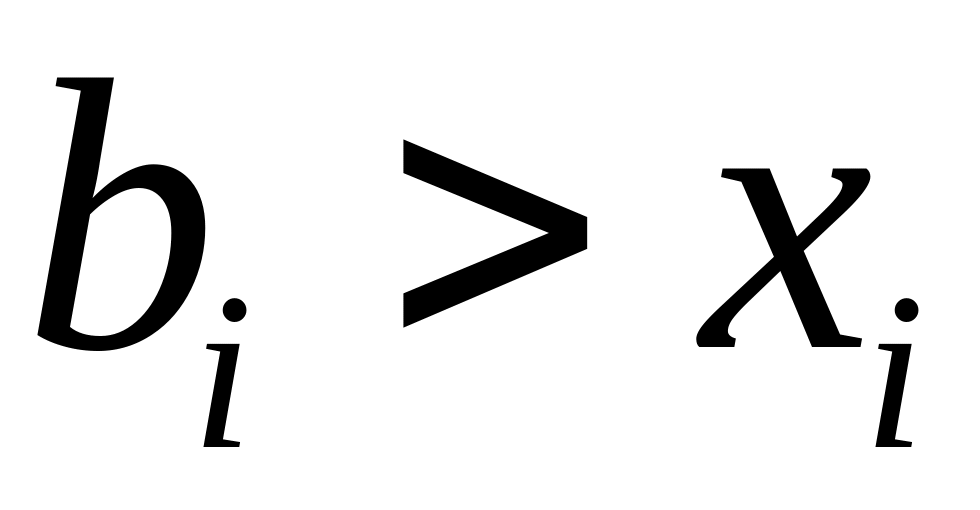Лемма (Гейла). Пусть ограниченное, полунепрерывное сверху множественнозначное отображ. симплекса в , удовлет-щее усл:

1. есть непустое выпуклое множество для всех ;

2. Для всех скалярное произведение Тогда существуют такие и , что .

27. Сущ-вание конкурентного равновесия в модели Эрроу-Дебре.

Условия существования модели Эрроу-Дебре:

1. Мн-во компактно в и содержит нулевой вектор .

2. Множество выпукло в .

3. Мн-во зам-то и выпукло в причем, если для , то для всех .

4. Ф. пол-сти непр-но диф-ма на и строго вогнута .

5. Функция обладает свойством ненасыщаемости .

6. Существует , для которого , Теорема: В модели Эрроу-Дебре существует конкурентное равновесие, если выполняются условия 1)-6).Доказательство: Пусть для каждого . (5). Как следует из условий 1. и 5., множество 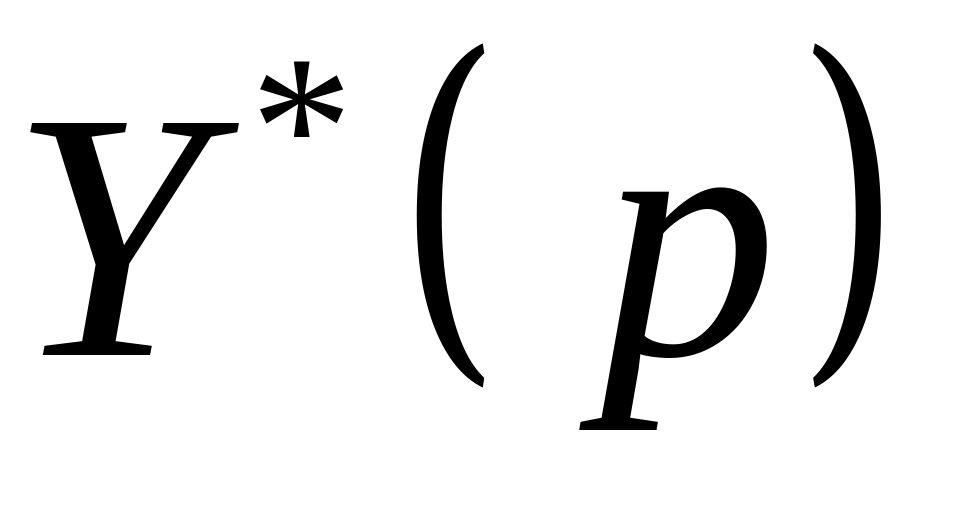есть непустое, компактное и выпуклое множество. Обозначим через отображение . Из непрерывности (линейности) функций , 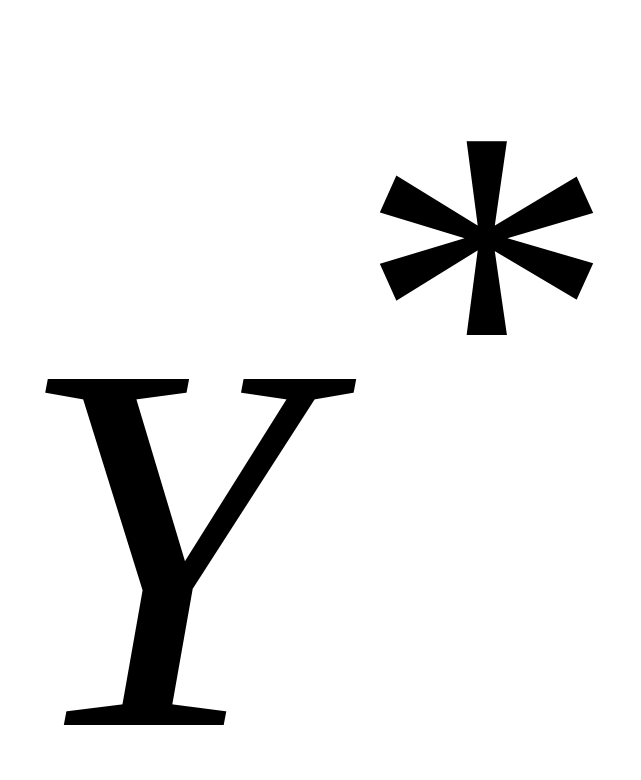есть ограниченное, полунепрерывное сверху отображение. Исходя из того, что , задача (2) должна решаться при ограничении (6) где 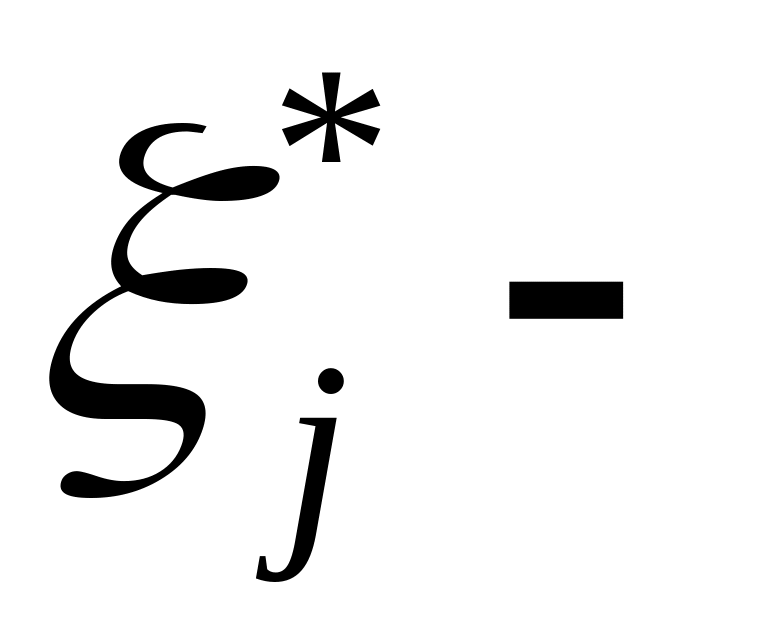оптимальное решение задачи (1). Имеет место строгое равенство: (7)Если это не так, то в силу условия 5 существует , для которого

, а по условию 4 можно найти такое

, где , что , причем все еще удовлетворяет ограничениям (6). Но это противоречит определению как точки максимума. Таким образом, равенство (7) действительно имеет место. Т.к. по условию 1 , то по определению максимума . Отсюда и из условий 1-6 следует, что множество оптимальных решений задачи (2) при ограничениях (6) есть непустой выпуклый компакт. Поэтому множество также будет непустым выпуклым компактом. Так же есть полунепрерывное сверху множественнозначное отображение. Построим отображение для любого следующим образом:

(8)

где 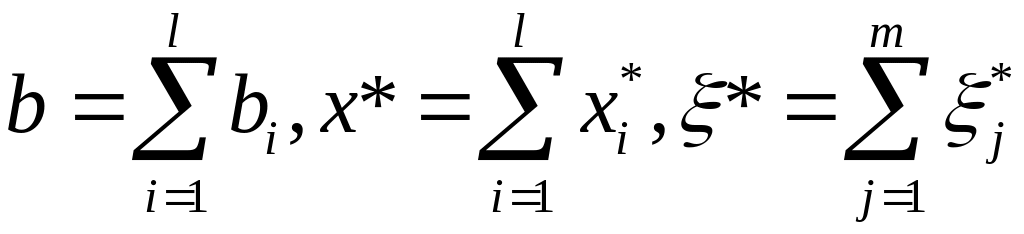Как и выше, можно показать, что есть ограниченное, полунепрерывное сверху множественнозначное отображение из в и что множество не пусто, выпукло и замкнуто. Суммируя обе стороны равенства (7) по , получаем 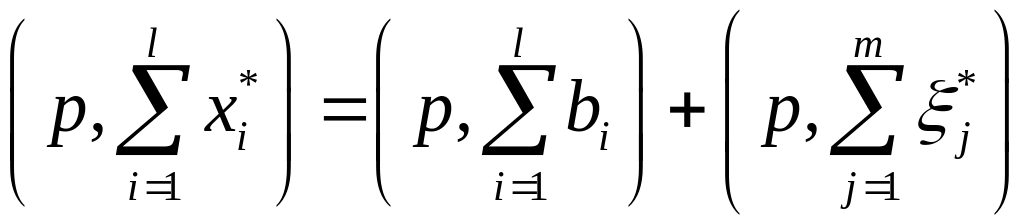или

В обозначениях элементов множества это равенство записывается как (9). Видно, что отображение S, порождающее для каждого множество (8). Следовательно существует такое и , что . Поэтому набор векторов , где , образует конкурентное равновесие в модели Эрроу-Дебре. Действительно, условие (6) выполнено по построению векторов и ; условие (7) следует из неравенства ; условие (8) вытекает из (9) и, наконец, отображения и являются функциями совокупных спроса и предложения в модели Эрроу-Дебре, так как они определены посредством соотношений (3), (4). ■