
- •1. Отношение предпочтения и функция полезности (свойства).
- •2.Эластичность функций. Свойства эластичности.
- •3. Предельная норма замещения товаров и услуг.
- •4. Предельная норма замещения товаров и услуг.
- •5. Бюджетное множество. Задача потребительского выбора.
- •6.Решение задачи потребителя в случае двух товаров.
- •7. Функция спроса и ее свойства.
- •8.Основное матричное уравнение теории потребления. Уравнение Слуцкого.
- •9. Основное матричное уравнение теории потребления. Типы товаров.
- •10.Определение, свойства, примеры производственных функций.
- •11. Эластичность в теории производства.
- •12.Предельная норма замещения в теории производства.
- •13. Математические модели задачи фирмы.
- •14. Решение задачи фирмы.
- •15. Геометрическое иллюстрация решения задачи фирмы
- •16. Основное матричное уравнение фирмы.
- •17 Анализ основного матричного уравнения фирмы
- •18. Моделирование ценообразования при монополии.
- •19. Математическая модель олигополии.
- •20. Анализ дуополии Курно.
- •22. Модель дуополии Штакельберга. Сравнение равновесия Штакельберга с равновесием Курно.
- •23.Сговор. Сравнение равновесного выпуска при сговоре с суммарным выпуском при равновесии Курно.
- •24. Картель. Сравнение равновесного выпуска при картеле с суммарным выпуском при равновесии Курно.
- •25.Конкурентное равновесие. Модель Вальраса.
- •26. Модель Эрроу-Дебре. Лемма Гейла.
- •28. Экономика благосостояния и оптимум Парето.
- •29. Модель конкурентного равновесия с фиксированными доходами.
- •30.Алгоритмы формирования цен. Паутинообразная модель.
- •31. Модель Неймана, ее характеристики. Луч Неймана.
- •32.Луч Неймана. Существование равновесия модели Неймана
- •33. Оптимальная траектория. Понятие магистрали. Теорема Моришимы о магистрали.
- •34. Алгоритмы построения оптимальной траектории.
24. Картель. Сравнение равновесного выпуска при картеле с суммарным выпуском при равновесии Курно.
Если на рынке допустимо перераспределение прибылей между олигополистами, то им выгодно выбирать такой объем производства, который максимизирует суммарную прибыль. Такое объединение олигополистов называется картель.
Т.к. фирмы могут распределять прибыль и целевая функция олигополистов квазилинейна по деньгам, то максимум суммарной прибыли есть Парето – оптимум олигополии. . Фактически картель действует как монополия, однако следует несколько изменить модель, по сравнению со случаем обычной монополии, т.к. у каждой из входящих в картель фирм своя функция издержек.
Суммарная прибыль
имеет вид:
 (1),
(1),
![]() -суммарный
объем выпуска. Тогда, продифференцировав
(1) по выпускам всех фирм, получим
дифференциальную характеристику
картеля:
-суммарный
объем выпуска. Тогда, продифференцировав
(1) по выпускам всех фирм, получим
дифференциальную характеристику
картеля:
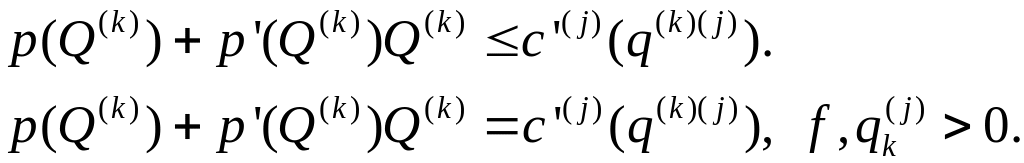
Картель распределит объемы производства между предприятиями при положительных объемах выпуска, чтобы предельные издержки были равными.
Пример.
Пусть
![]() а функции издержек имеют вид:
а функции издержек имеют вид:
![]() Объем производства картеля определяется
соотношением :
Объем производства картеля определяется
соотношением :
![]() .
.
Таким
образом, он равен
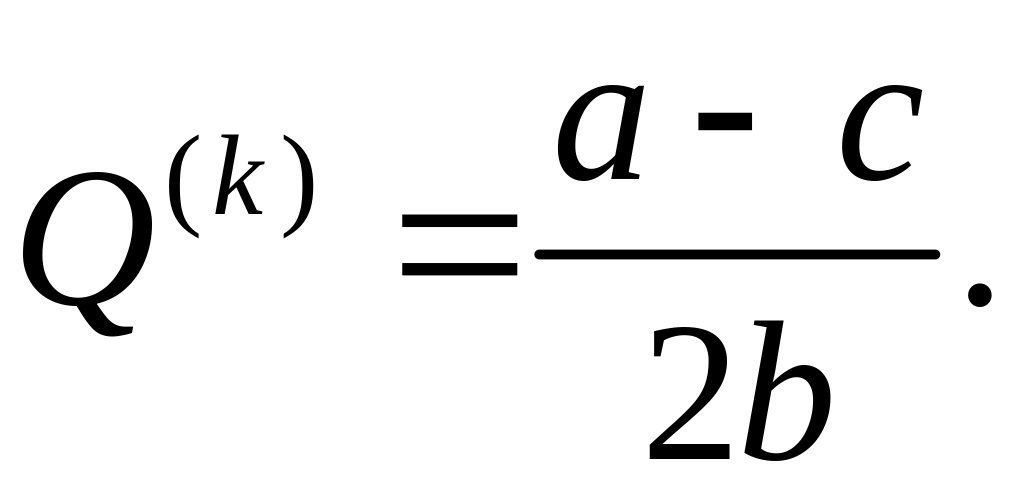
Прибыль
картеля -

Если
решать данную задачу в равновесии Курно,
то суммарный объем производства равен:
 а суммарная прибыль
а суммарная прибыль
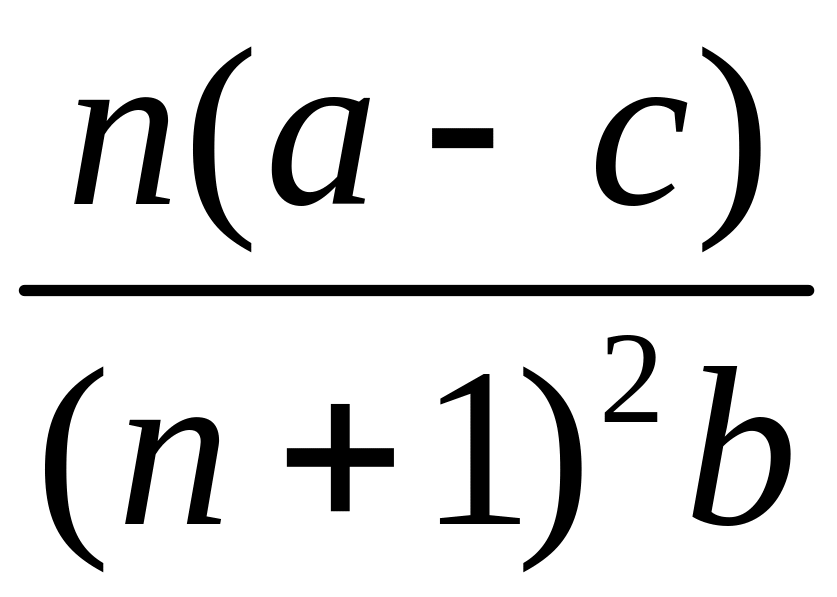 ,
откуда ясна неоптимальность равновесия
Курно с точки зрения производителей.
Они могли бы получать больше прибыли,
если бы производили меньше.
,
откуда ясна неоптимальность равновесия
Курно с точки зрения производителей.
Они могли бы получать больше прибыли,
если бы производили меньше.
Теорема 1. Пусть:
Равновесия в модели Курно и модели картеля существуют и все фирмы производят продукцию в положительных количествах:
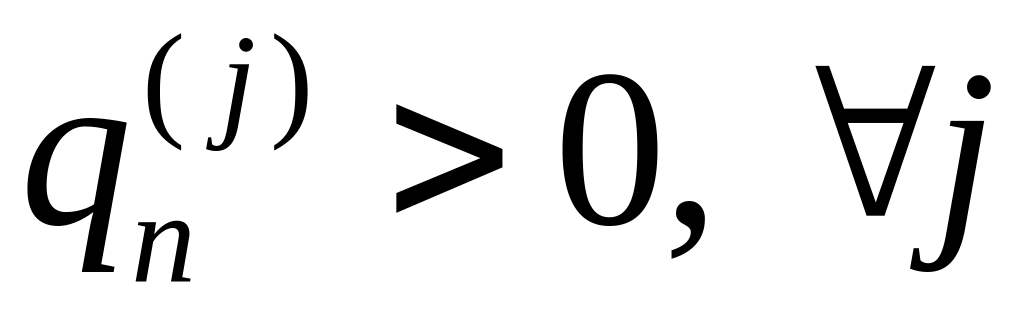 .
.Обратная функция спроса убывает и дифференцируема.
Функция издержек
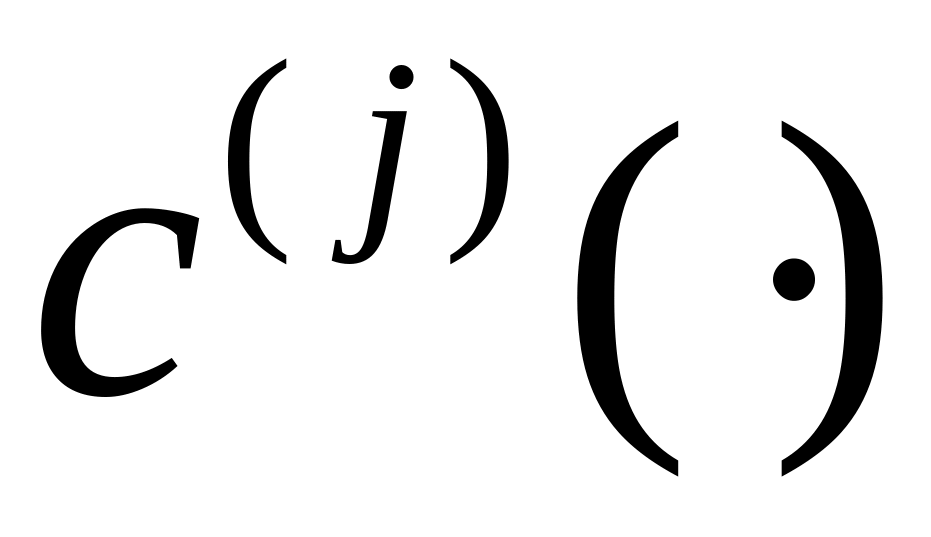 дифференцируема и выпукла.
дифференцируема и выпукла.
Тогда
в точке картеля суммарный выпуск
продукции меньше, чем в равновесии
Курно:![]()
Зам. Картель, как и рассматр-мый ранее сговор явл. неустойчивым, если нет способа гарантировать выпол. соглашения между фирмами. Теорема 2. Пусть:
В картеле все фирмы производят продукцию в положительных количествах: .
Обратная функция спроса убывает и дифференцируема.
Функции издержек дифференцируемы.
Тогда
в точке картеля
 т.е. каждая фирма может повысить свою
прибыль увеличив свой выпуск.
т.е. каждая фирма может повысить свою
прибыль увеличив свой выпуск.
Доказательство.
Производная
функция прибыли
![]() го
участника по всему выпуску равна:
го
участника по всему выпуску равна:

Учитывая
дифференциальные характеристики точки
![]()
![]()

Т.о.
если достигнуты соглашения о квотах
выпуска
![]() максимизирующих суммарную прибыли, то
каждой фирме выгодно (по крайней мере
локально) производить больше своей
квоты.
максимизирующих суммарную прибыли, то
каждой фирме выгодно (по крайней мере
локально) производить больше своей
квоты.
25.Конкурентное равновесие. Модель Вальраса.
Рассмотрим
расширенное пространство товаров
![]() ,
и вектор
,
и вектор
![]() ,
где компонентой данного вектора явл
как затраты так и выпуск компоненты,
кот для соотв затрат будут с отрицательным
знаком. Если вектор x
явл вектором чистого выпуска, то
компоненты соот-щие затратам будут =0.
В модели Вальраса каждый потребитель
с номером
,
где компонентой данного вектора явл
как затраты так и выпуск компоненты,
кот для соотв затрат будут с отрицательным
знаком. Если вектор x
явл вектором чистого выпуска, то
компоненты соот-щие затратам будут =0.
В модели Вальраса каждый потребитель
с номером
![]() будет характеризоваться 3 показателями:
будет характеризоваться 3 показателями:
Начальный запас товаров, кот он может продавать
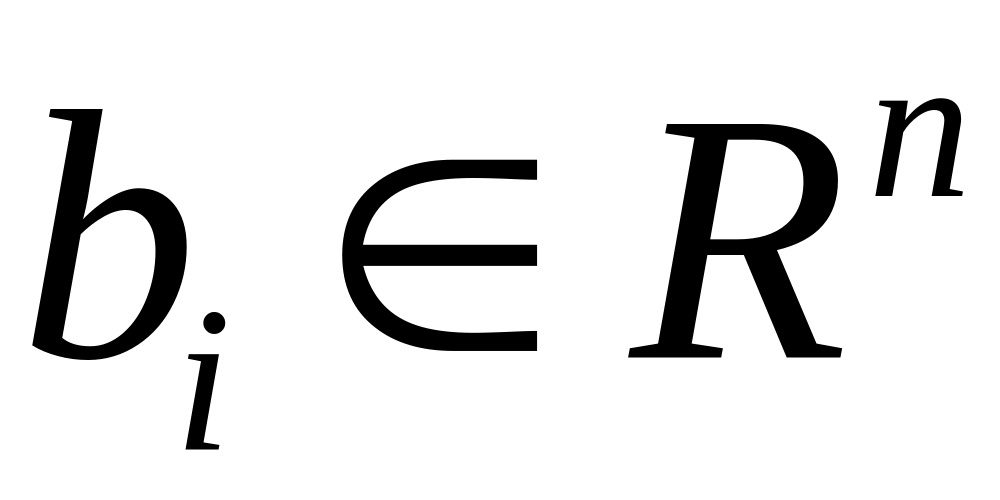 ,
, функция дохода
потребителя,
функция дохода
потребителя, вектор ф-ции спроса
на продукты производства.
вектор ф-ции спроса
на продукты производства.
Каждый
![]() -ый
производитель характеризуется мн-вом
вида
-ый
производитель характеризуется мн-вом
вида
![]() .
Данное множество наз мн-вом оптимальных
производственных планов. Данное мн-во
состоит из след элементов
.
Данное множество наз мн-вом оптимальных
производственных планов. Данное мн-во
состоит из след элементов
![]() ,
где
,
где
![]() некоторая ф-ция производителя,
некоторая ф-ция производителя,
![]() -
вектор ф-ция спроса на затраты,
-
вектор ф-ция спроса на затраты,
![]() -
вектор ф-ция предложения готовой
продукции. Мат модель будет иметь вид
-
вектор ф-ция предложения готовой
продукции. Мат модель будет иметь вид
![]() ,
(1) где
,
(1) где
![]() -
про-во цен всех товаров,
-
про-во цен всех товаров,
![]() -
мн-во всех участников рынка,
-
мн-во всех участников рынка,
![]() ,
где
,
где
![]() -кол-во
потребителей,
-кол-во
потребителей,
![]() -
кол-во производителей.
-
кол-во производителей.
Замечание: Т.к. каждый участник рынка может выступать в роли продавца и покупателя, то число продавцов и покупателей для разных товаров будет различным.
Весь доход полученный от реализации продукции на рынке
распред м/у
потребителями след образом
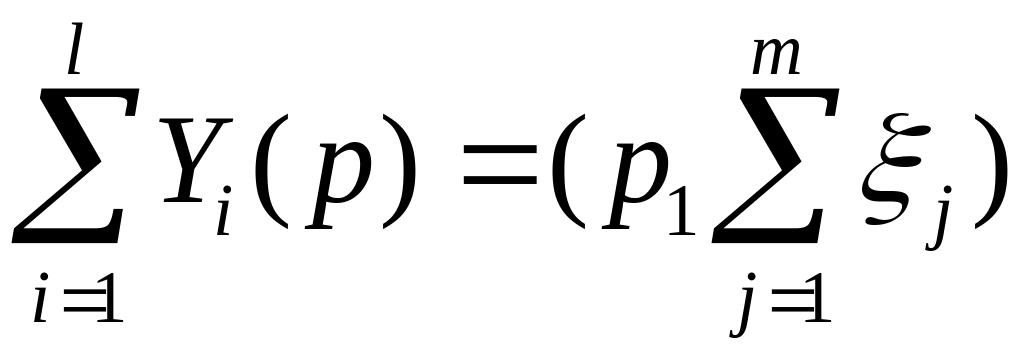 ,
,
![]() скалярное произведение показывает на
прибыль всего производственного цикла,
скалярное произведение показывает на
прибыль всего производственного цикла,
![]() -
оптимальный план
-го
производителя. Ф-ция
совокупного спроса модели Вальраса
наз ф-ция, кот принимать мн-во
-
оптимальный план
-го
производителя. Ф-ция
совокупного спроса модели Вальраса
наз ф-ция, кот принимать мн-во
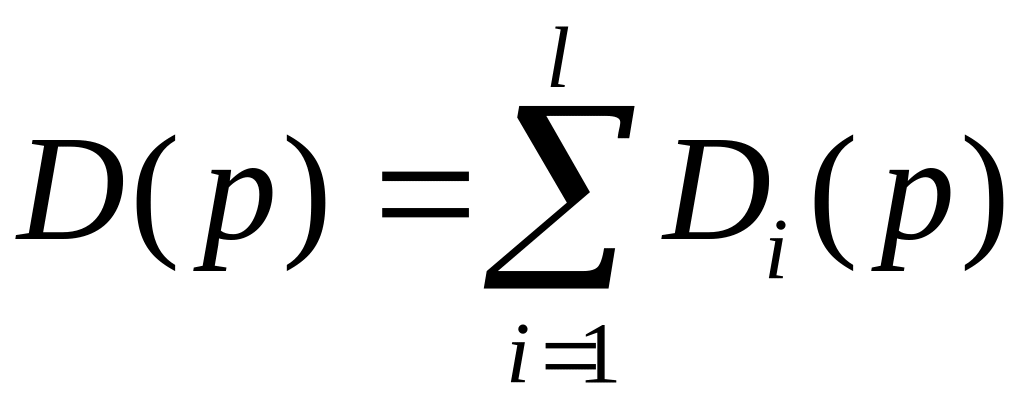 Ф-ция
предложения модели Вальраса
Ф-ция
предложения модели Вальраса
 .
С учетом формул спроса и предложения
модель рынка (1) перепишется в виде
.
С учетом формул спроса и предложения
модель рынка (1) перепишется в виде
![]() (2)
(2)
Введем обозначения
![]() -
совокупность спроса соот-щей цене p,
-
совокупность спроса соот-щей цене p,
![]() -
совокупное предложение соот-щее цене
p.
Данный вариант является оптимальной
ситуацией совокупного продавца и
совокупного покупателя на рынке
установленных цен. Если x>y,
то на рынке наблюдается дефицит товаров,
в противном случае его излишек.
-
совокупное предложение соот-щее цене
p.
Данный вариант является оптимальной
ситуацией совокупного продавца и
совокупного покупателя на рынке
установленных цен. Если x>y,
то на рынке наблюдается дефицит товаров,
в противном случае его излишек.
Опр.
Тройка векторов вида
![]() называется конкурентным равновесием
соответствующим рынку (2),
если
называется конкурентным равновесием
соответствующим рынку (2),
если
![]() (3), причем
(3), причем
![]() ,(4)
,(4)
![]() .
(5)
.
(5)
![]() -
равновесный вектор цен.
-
равновесный вектор цен.
По определению
совокупного спроса и предложения следует
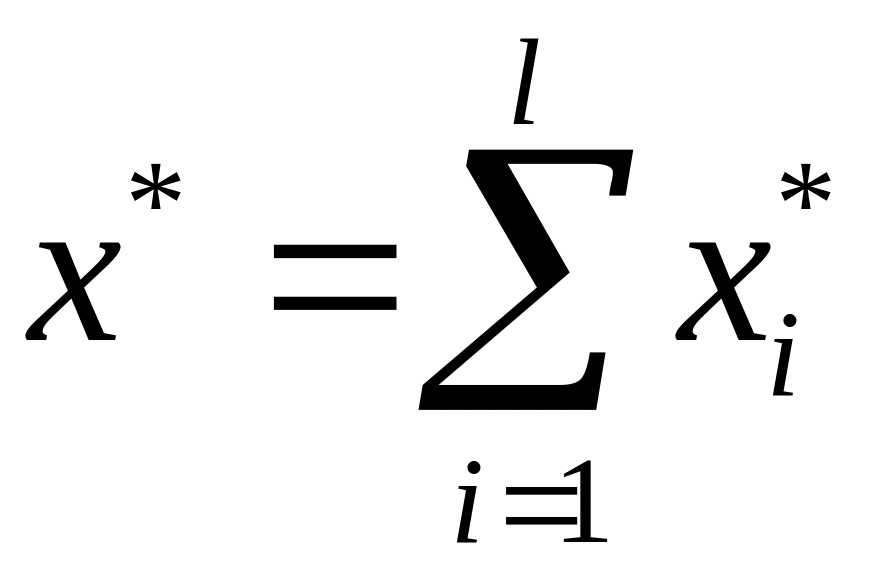 ,
,
![]() ,
,
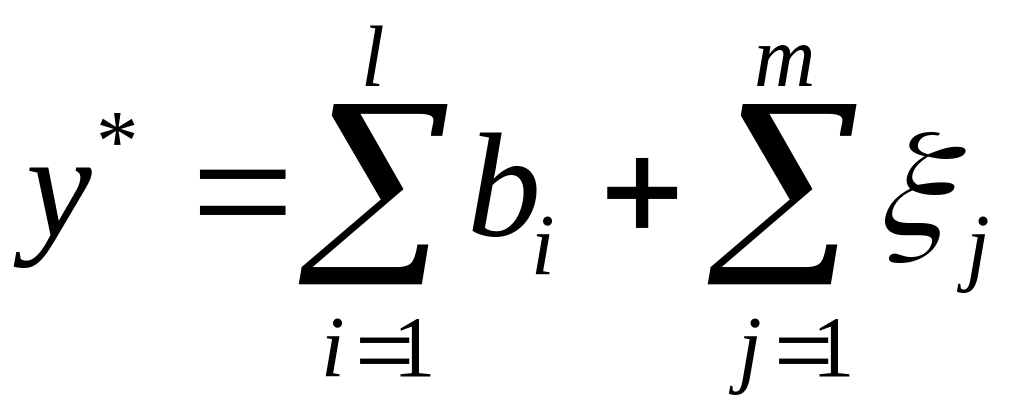 ,
,
![]() .
Тогда (3)-(5)
будет иметь вид
.
Тогда (3)-(5)
будет иметь вид
![]() (6)
(6)
![]() (7)
(7)
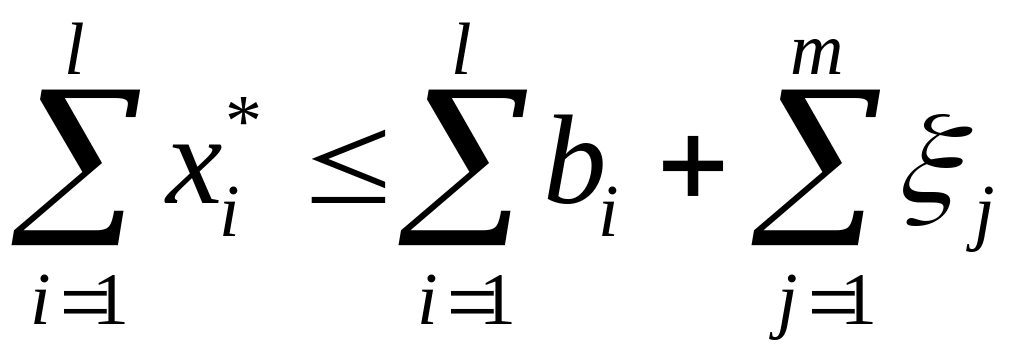 (8)
(8)
Экономический смысл: (3) показывает, что на цены каждый потребитель и производитель реагирует наилучшим образом. Это следует из (6),(7), (4) и требует, чтобы совокупное предложение не было меньше совокупного спроса. (5) требует, чтобы совокупный спрос = совокупному предложению
