Отношение предпочтения и функция полезности (свойства).
Эластичность функций. Свойства эластичностей.
Кривые безразличия взаимодополняемых товаров. Предельная норма замещения товаров и услуг.
Кривые безразличия взаимозаменяемых товаров. Предельная норма замещения товаров и услуг.
Бюджетное множество. Задача потребительского выбора.
Решение задачи потребителя в случае двух товаров.
Функция спроса и ее свойства.
Основное матричное уравнение теории потребления. Уравнение Слуцкого.
Основное матричное уравнение теории потребления. Типы товаров.
Определение, свойства примеры производственных функций.
Эластичность в теории производства.
Предельная норма замещения в теории производства.
Математические модели задачи фирмы.
Решение задачи фирмы.
Геометрическое решение задачи фирмы.
Основное матричное уравнение фирмы.
Анализ основного матричного уравнения фирмы.
Моделирование ценообразования при монополии.
Математическая модель олигополии.
Анализ дуополии Курно.
Свойства равновесия Курно в случае постоянных издержек.
Модель дуополии Штакельберга. Сравнение равновесия Штакельберга с равновесием Курно.
Сговор. Сравнение равновесного выпуска при сговоре с суммарным выпуском при равновесии Курно.
Картель. Сравнение равновесного выпуска при картеле с суммарным выпуском при равновесии Курно.
Конкурентное равновесие. Модель Вальраса.
Модель Эрроу-Дебре. Лемма Гейла.
Существование конкурентного равновесия в модели Эрроу-Дебре.
Экономика благосостояния и оптимум Парето.
Модель конкурентного равновесия с фиксированными доходами.
Алгоритмы формирования цен. Паутинообразная модель.
Модель Неймана. Луч Неймана.
Луч Неймана. Существование равновесия в модели Неймана.
Оптимальная траектория. Понятие магистрали. Теорема Моришимы о магистрали.
Алгоритмы построения оптимальной траектории.
1. Отношение предпочтения и функция полезности (свойства).
Пусть
- некоторое выпуклое множество, на
котором определены интересы потребителя,
и пусть есть два набора товаров.
Потребитель различает данные наборы
предпочитая один набор товаров другому.
Запись
означает,
что потребитель предпочитает набор
набору
, либо не делает между ними различия.
Считается, что отношение предпочтения удовлетворяет следующим свойствам (аксиомам):
1. (рефлективность):
для любого
,
справедливо
;
2. (транзитивность):
для любых
,
из отношений
и
, следует что
;
3. (аксиома
совершенства): для любой пары
, либо
, либо
, либо и то и другое.
Опр:
Для любого
множество
называется множеством безразличия;
множество
множеством предпочтений; множество
множеством непредпочтений.
4. (аксиома
непрерывности): для каждого
множество строгого предпочтения
и строгого непредпочтения
являются открытыми в
;
5. (ненасыщение):
для двух заданных наборов из условия
,
следует
, причем если
, то
. Эта аксиома означает, что если в наборе
количество каждого товара не меньше
чем в наборе
, причем хотя бы одного товара в наборе
больше, чем в наборе
, то набор
предпочтительнее набору
;
Опр: Точкой насыщения называется наиболее предпочтительный набор , т.е. такой, что .
6. (аксиома
выпуклости): если
,
то
выполняется соотношение
, где
набор, состоящий из
единиц i-го товара.
Опр:
Функция
,
определенная на множестве
,
называется функцией полезности,
соответствующей отношению предпочтения,
если
,тогда и только тогда, когда
.
Свойства функции
полезности
отношения предпочтения.
1. Если непрерывно
дифференцируемая функция, то из аксиомы
ненасыщения следует положительность
ее первых частных производных
, т.е. в любой точке пространства
возрастание
потребления любого товара при постоянном
потреблении остальных приводит к
увеличению полезности.
Опр:
Вектор
обозначим через
и называют вектором предельных
полезностей, а частную производную
предельной полезностью го товара.
2. Небольшое
увеличение
го
товара при его первоначальном отсутствии
резко увеличивает его полезность, т.е.
3. При очень большом
количестве
го
товара, его дальнейшее увеличение не
приводит к увеличению его полезности,
т.е.
4. Если дважды непрерывно дифф-руемая функция, то из аксиомы выпуклости следует, что матрица вторых производных функции (матрица Гессе) должна быть отрицательно определена, т.е.
В частности имеет
место закон Гессена: предельная полезность
любого товара уменьшается по мере того,
как продукт потребляется, т.е.
.
2.Эластичность функций. Свойства эластичности.
Эластичность
функций
называется предел отношения относительно
переменных
и
.
(1)
-
предельное значение функции в точке
.
-
среднее значение функции в точке
.
Геометрический смысл: Предположим, что имеется ед. спроса на 1 товар.
-
произвольная точка данного графика.
Проведем через данную точку касательную,
где
-угол
наклонности.
,
Рассм.
и
данные треугольники являются подобными.
Тогда
.
Опр:
Если
,
то функция называется эластичной по
переменной
.
,
то функция называется неэластичной.
,
то функция называется функцией с
единичной эластичностью.
Функция с бесконечной эластичностью называется совершенно эластично, а с нулевой эластичностью совершенно не эластично.
Виды эластичности:
Конечная эластичность
Дуговая или средняя
Логарифмическая
Свойства эластичности:
Эластичность является безразмерной величиной, т.е. её значение не зависит от единиц измерения переменных и .
Док-во
:
Эластичность взаимообратных функций явл. взаимообратными величинами.
.
Док-во :
Эластичность произвольных функций зависящих от одного и того же аргумента равняется сумме эластичностей этих функций.
Эластичность отношений двух функций, зависящих от одного и того же аргумента равняется разности эластичности этих функций.
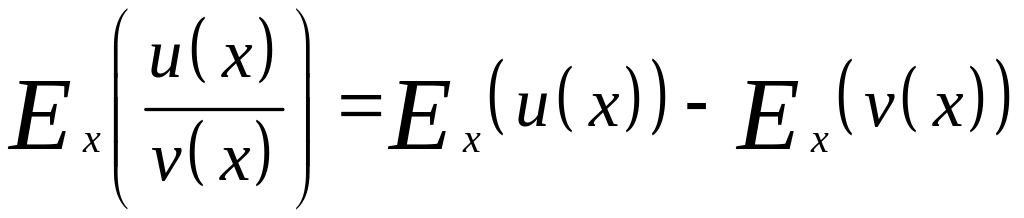
Эластичность суммы двух функций зависящих от одного и того же элемента.
